travelling salesman problem javatpoint

Graph Theory

Control System

• Interview Q

Discrete Mathematics

Sets Theory

Functions & algorithms, logic & propositional, counting techniques, recurrence relations, probability theory, binary trees, operator & postulates, group theory, ordered sets & lattices, boolean algebra.

• Send your Feedback to [email protected]

Help Others, Please Share

Learn Latest Tutorials

Transact-SQL

Reinforcement Learning

R Programming

React Native

Python Design Patterns

Python Pillow

Python Turtle

Preparation

Verbal Ability

Interview Questions

Company Questions

Trending Technologies

Artificial Intelligence

Cloud Computing

Data Science

Machine Learning

B.Tech / MCA

Data Structures

Operating System

Computer Network

Compiler Design

Computer Organization

Ethical Hacking

Computer Graphics

Software Engineering

Web Technology

Cyber Security

C Programming

Data Mining

Data Warehouse

• Data Structures & Algorithms
• DSA - Overview
• DSA - Environment Setup
• DSA - Algorithms Basics
• DSA - Asymptotic Analysis
• Data Structures
• DSA - Data Structure Basics
• DSA - Data Structures and Types
• DSA - Array Data Structure
• Linked Lists
• DSA - Linked List Data Structure
• DSA - Doubly Linked List Data Structure
• DSA - Circular Linked List Data Structure
• Stack & Queue
• DSA - Stack Data Structure
• DSA - Expression Parsing
• DSA - Queue Data Structure
• Searching Algorithms
• DSA - Searching Algorithms
• DSA - Linear Search Algorithm
• DSA - Binary Search Algorithm
• DSA - Interpolation Search
• DSA - Jump Search Algorithm
• DSA - Exponential Search
• DSA - Fibonacci Search
• DSA - Sublist Search
• DSA - Hash Table
• Sorting Algorithms
• DSA - Sorting Algorithms
• DSA - Bubble Sort Algorithm
• DSA - Insertion Sort Algorithm
• DSA - Selection Sort Algorithm
• DSA - Merge Sort Algorithm
• DSA - Shell Sort Algorithm
• DSA - Heap Sort
• DSA - Bucket Sort Algorithm
• DSA - Counting Sort Algorithm
• DSA - Radix Sort Algorithm
• DSA - Quick Sort Algorithm
• Graph Data Structure
• DSA - Graph Data Structure
• DSA - Depth First Traversal
• DSA - Breadth First Traversal
• DSA - Spanning Tree
• Tree Data Structure
• DSA - Tree Data Structure
• DSA - Tree Traversal
• DSA - Binary Search Tree
• DSA - AVL Tree
• DSA - Red Black Trees
• DSA - B Trees
• DSA - B+ Trees
• DSA - Splay Trees
• DSA - Tries
• DSA - Heap Data Structure
• DSA - Recursion Algorithms
• DSA - Tower of Hanoi Using Recursion
• DSA - Fibonacci Series Using Recursion
• Divide and Conquer
• DSA - Divide and Conquer
• DSA - Max-Min Problem
• DSA - Strassen's Matrix Multiplication
• DSA - Karatsuba Algorithm
• Greedy Algorithms
• DSA - Greedy Algorithms
• DSA - Travelling Salesman Problem (Greedy Approach)
• DSA - Prim's Minimal Spanning Tree
• DSA - Kruskal's Minimal Spanning Tree
• DSA - Dijkstra's Shortest Path Algorithm
• DSA - Map Colouring Algorithm
• DSA - Fractional Knapsack Problem
• DSA - Job Sequencing with Deadline
• DSA - Optimal Merge Pattern Algorithm
• Dynamic Programming
• DSA - Dynamic Programming
• DSA - Matrix Chain Multiplication
• DSA - Floyd Warshall Algorithm
• DSA - 0-1 Knapsack Problem
• DSA - Longest Common Subsequence Algorithm
• DSA - Travelling Salesman Problem (Dynamic Approach)
• Approximation Algorithms
• DSA - Approximation Algorithms
• DSA - Vertex Cover Algorithm
• DSA - Set Cover Problem
• DSA - Travelling Salesman Problem (Approximation Approach)
• Randomized Algorithms
• DSA - Randomized Algorithms
• DSA - Randomized Quick Sort Algorithm
• DSA - Karger’s Minimum Cut Algorithm
• DSA - Fisher-Yates Shuffle Algorithm
• DSA Useful Resources
• DSA - Questions and Answers
• DSA - Quick Guide
• DSA - Useful Resources
• DSA - Discussion
• Selected Reading
• UPSC IAS Exams Notes
• Developer's Best Practices
• Questions and Answers
• Effective Resume Writing
• HR Interview Questions
• Computer Glossary

Travelling Salesman Problem (Greedy Approach)

Travelling salesperson algorithm.

The travelling salesman problem is a graph computational problem where the salesman needs to visit all cities (represented using nodes in a graph) in a list just once and the distances (represented using edges in the graph) between all these cities are known. The solution that is needed to be found for this problem is the shortest possible route in which the salesman visits all the cities and returns to the origin city.

If you look at the graph below, considering that the salesman starts from the vertex ‘a’, they need to travel through all the remaining vertices b, c, d, e, f and get back to ‘a’ while making sure that the cost taken is minimum.

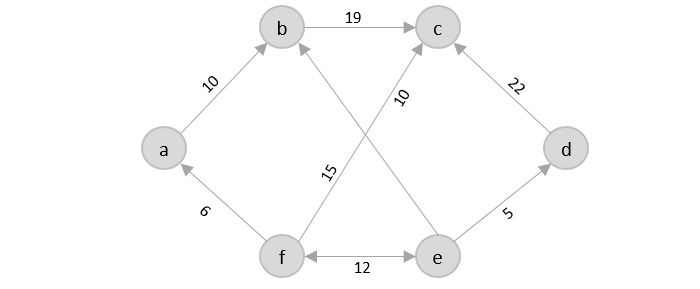
There are various approaches to find the solution to the travelling salesman problem: naive approach, greedy approach, dynamic programming approach, etc. In this tutorial we will be learning about solving travelling salesman problem using greedy approach.

As the definition for greedy approach states, we need to find the best optimal solution locally to figure out the global optimal solution. The inputs taken by the algorithm are the graph G {V, E}, where V is the set of vertices and E is the set of edges. The shortest path of graph G starting from one vertex returning to the same vertex is obtained as the output.

Travelling salesman problem takes a graph G {V, E} as an input and declare another graph as the output (say G’) which will record the path the salesman is going to take from one node to another.

The algorithm begins by sorting all the edges in the input graph G from the least distance to the largest distance.

The first edge selected is the edge with least distance, and one of the two vertices (say A and B) being the origin node (say A).

Then among the adjacent edges of the node other than the origin node (B), find the least cost edge and add it onto the output graph.

Continue the process with further nodes making sure there are no cycles in the output graph and the path reaches back to the origin node A.

However, if the origin is mentioned in the given problem, then the solution must always start from that node only. Let us look at some example problems to understand this better.

Consider the following graph with six cities and the distances between them −

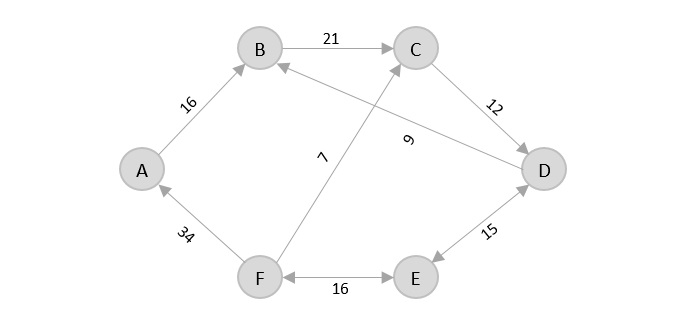
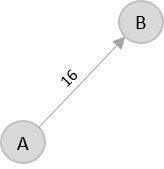
From the given graph, since the origin is already mentioned, the solution must always start from that node. Among the edges leading from A, A → B has the shortest distance.

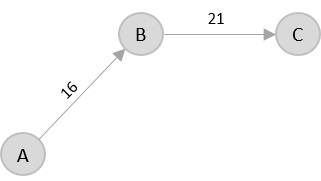
Then, B → C has the shortest and only edge between, therefore it is included in the output graph.

There’s only one edge between C → D, therefore it is added to the output graph.

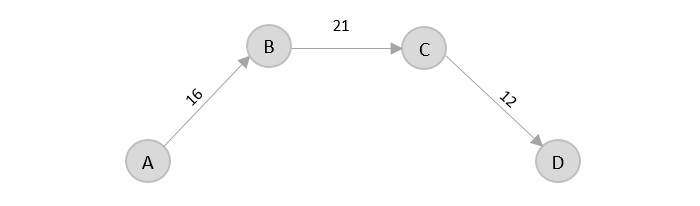
There’s two outward edges from D. Even though, D → B has lower distance than D → E, B is already visited once and it would form a cycle if added to the output graph. Therefore, D → E is added into the output graph.

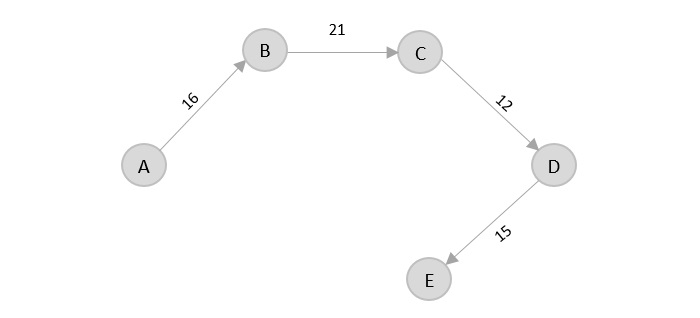
There’s only one edge from e, that is E → F. Therefore, it is added into the output graph.

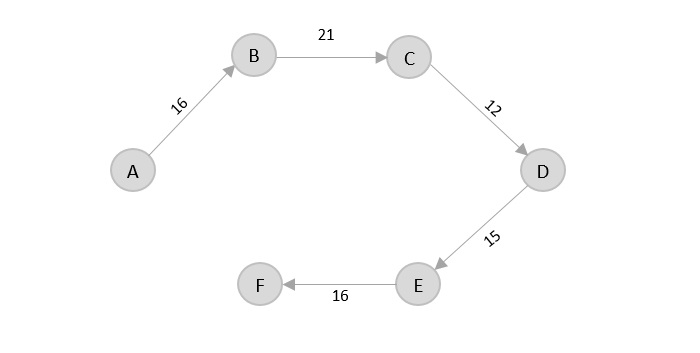
Again, even though F → C has lower distance than F → A, F → A is added into the output graph in order to avoid the cycle that would form and C is already visited once.

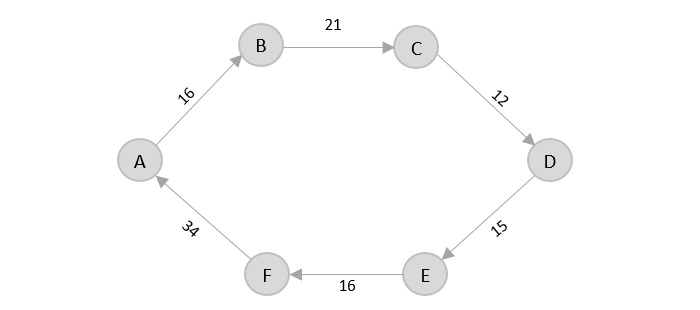
The shortest path that originates and ends at A is A → B → C → D → E → F → A

The cost of the path is: 16 + 21 + 12 + 15 + 16 + 34 = 114.

Even though, the cost of path could be decreased if it originates from other nodes but the question is not raised with respect to that.

The complete implementation of Travelling Salesman Problem using Greedy Approach is given below −

• Analysis of Algorithms
• Backtracking
• Dynamic Programming
• Divide and Conquer
• Geometric Algorithms
• Mathematical Algorithms
• Pattern Searching
• Bitwise Algorithms
• Branch & Bound
• Randomized Algorithms
• Branch and Bound Algorithm
• Introduction to Branch and Bound - Data Structures and Algorithms Tutorial
• 0/1 Knapsack using Branch and Bound
• Implementation of 0/1 Knapsack using Branch and Bound
• 8 puzzle Problem using Branch And Bound
• Job Assignment Problem using Branch And Bound
• N Queen Problem using Branch And Bound

Traveling Salesman Problem using Branch And Bound

Given a set of cities and distance between every pair of cities, the problem is to find the shortest possible tour that visits every city exactly once and returns to the starting point.  

For example, consider the graph shown in figure on right side. A TSP tour in the graph is 0-1-3-2-0. The cost of the tour is 10+25+30+15 which is 80. We have discussed following solutions  1) Naive and Dynamic Programming   2) Approximate solution using MST      Branch and Bound Solution   As seen in the previous articles, in Branch and Bound method, for current node in tree, we compute a bound on best possible solution that we can get if we down this node. If the bound on best possible solution itself is worse than current best (best computed so far), then we ignore the subtree rooted with the node.  Note that the cost through a node includes two costs.  1) Cost of reaching the node from the root (When we reach a node, we have this cost computed)  2) Cost of reaching an answer from current node to a leaf (We compute a bound on this cost to decide whether to ignore subtree with this node or not).  

• In cases of a maximization problem , an upper bound tells us the maximum possible solution if we follow the given node. For example in 0/1 knapsack we used Greedy approach to find an upper bound .
• In cases of a minimization problem , a lower bound tells us the minimum possible solution if we follow the given node. For example, in Job Assignment Problem , we get a lower bound by assigning least cost job to a worker.

In branch and bound, the challenging part is figuring out a way to compute a bound on best possible solution. Below is an idea used to compute bounds for Travelling salesman problem. Cost of any tour can be written as below.  

For example, consider the above shown graph. Below are minimum cost two edges adjacent to every node.   

Now we have an idea about computation of lower bound. Let us see how to how to apply it state space search tree. We start enumerating all possible nodes (preferably in lexicographical order) 1. The Root Node: Without loss of generality, we assume we start at vertex “0” for which the lower bound has been calculated above. Dealing with Level 2: The next level enumerates all possible vertices we can go to (keeping in mind that in any path a vertex has to occur only once) which are, 1, 2, 3… n (Note that the graph is complete). Consider we are calculating for vertex 1, Since we moved from 0 to 1, our tour has now included the edge 0-1. This allows us to make necessary changes in the lower bound of the root.   

How does it work? To include edge 0-1, we add the edge cost of 0-1, and subtract an edge weight such that the lower bound remains as tight as possible which would be the sum of the minimum edges of 0 and 1 divided by 2. Clearly, the edge subtracted can’t be smaller than this. Dealing with other levels: As we move on to the next level, we again enumerate all possible vertices. For the above case going further after 1, we check out for 2, 3, 4, …n.  Consider lower bound for 2 as we moved from 1 to 1, we include the edge 1-2 to the tour and alter the new lower bound for this node.  

Note: The only change in the formula is that this time we have included second minimum edge cost for 1, because the minimum edge cost has already been subtracted in previous level.   

Output :    

The rounding is being done in this line of code:

In the Branch and Bound TSP algorithm, we compute a lower bound on the total cost of the optimal solution by adding up the minimum edge costs for each vertex, and then dividing by two. However, this lower bound may not be an integer. To get an integer lower bound, we can use rounding.

In the above code, the curr_bound variable holds the current lower bound on the total cost of the optimal solution. When we visit a new vertex at level level, we compute a new lower bound new_bound by taking the sum of the minimum edge costs for the new vertex and its two closest neighbors. We then update the curr_bound variable by rounding new_bound to the nearest integer.

If level is 1, we round down to the nearest integer. This is because we have only visited one vertex so far, and we want to be conservative in our estimate of the total cost of the optimal solution. If level is greater than 1, we use a more aggressive rounding strategy that takes into account the fact that we have already visited some vertices and can therefore make a more accurate estimate of the total cost of the optimal solution.

Time Complexity: The worst case complexity of Branch and Bound remains same as that of the Brute Force clearly because in worst case, we may never get a chance to prune a node. Whereas, in practice it performs very well depending on the different instance of the TSP. The complexity also depends on the choice of the bounding function as they are the ones deciding how many nodes to be pruned. References:   http://lcm.csa.iisc.ernet.in/dsa/node187.html

Please Login to comment...

• 10 Best HuggingChat Alternatives and Competitors
• Best Free Android Apps for Podcast Listening
• Google AI Model: Predicts Floods 7 Days in Advance
• Who is Devika AI? India's 'AI coder', an alternative to Devin AI
• 30 OOPs Interview Questions and Answers (2024)

Improve your Coding Skills with Practice

What kind of Experience do you want to share?

• Gewinnspiel
• Interview QUESTION

DAA Tutorial

Asymptotic analysis, analysis away sorting, divide and conquer, lower bound theory, sorting is linear time, binary search trees, color black tree, dynamic programming, grabby algorithm, backtracking, shortest path, all-pairs shortest path, sorting networks, complexity class, approximation alpha, contents matching.

Interview Questions

• Send your Feedback to [email protected]

Help Others, Requested Portion

Learn Lastest Tutorials

Transact-SQL

Reinforcement Learning

R Programming

React Native

Python Design Patterns

Python Pillow

Python Turtle

Preparation

Verbal Ability

Company Questions

Trending Technologies

Artificial Intelligent

Cloud Computing

Your Science

Machine Learning

B.Tech / MCA

Data Structures

Operating System

Dedicated Network

Compiler Design

User Organization

Discrete Mathematics

Ethical Hacking

Your Visual

Software Engineering

Web Engineering

Cyber Security

C Programming

Control System

Data Mining

Data Stocks

Javatpoint Achievement

JavaTpoint offers too many high quality business. Mail us for festivity [email protected] , into get more information about given services.

• Website Designing
• Website Company
• Java Development
• PHP Development
• Graphics Designing
• Digital Marketing
• For Page and Off Folio SEO
• Contents Development
• Corporate Training
• Classroom and Online Training

Training In College Campus

JavaTpoint quotes college campus training on Core Espresso, Advance Java, .Net, Android, Hadoop, PHP, Web Engine and Page. Please mail your requirement at [email protected] . Duration: 1 week the 2 week

Travelling Salesman Problem: Python, C++ Algorithm

What is the Travelling Salesman Problem (TSP)?

Travelling Salesman Problem (TSP) is a classic combinatorics problem of theoretical computer science. The problem asks to find the shortest path in a graph with the condition of visiting all the nodes only one time and returning to the origin city.

The problem statement gives a list of cities along with the distances between each city.

Objective: To start from the origin city, visit other cities only once, and return to the original city again. Our target is to find the shortest possible path to complete the round-trip route.

Example of TSP

Here a graph is given where 1, 2, 3, and 4 represent the cities, and the weight associated with every edge represents the distance between those cities.

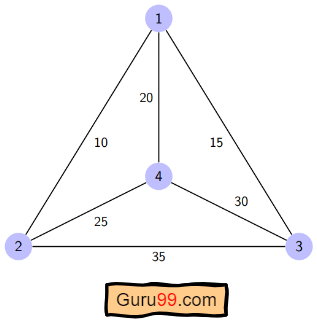
The goal is to find the shortest possible path for the tour that starts from the origin city, traverses the graph while only visiting the other cities or nodes once, and returns to the origin city.

For the above graph, the optimal route is to follow the minimum cost path: 1-2-4-3-1. And this shortest route would cost 10+25+30+15 =80

Different Solutions to Travelling Salesman Problem

Travelling Salesman Problem (TSP) is classified as a NP-hard problem due to having no polynomial time algorithm. The complexity increases exponentially by increasing the number of cities.

There are multiple ways to solve the traveling salesman problem (tsp). Some popular solutions are:

The brute force approach is the naive method for solving traveling salesman problems. In this approach, we first calculate all possible paths and then compare them. The number of paths in a graph consisting of n cities is n! It is computationally very expensive to solve the traveling salesman problem in this brute force approach.

The branch-and-bound method: The problem is broken down into sub-problems in this approach. The solution of those individual sub-problems would provide an optimal solution.

This tutorial will demonstrate a dynamic programming approach, the recursive version of this branch-and-bound method, to solve the traveling salesman problem.

Dynamic programming is such a method for seeking optimal solutions by analyzing all possible routes. It is one of the exact solution methods that solve traveling salesman problems through relatively higher cost than the greedy methods that provide a near-optimal solution.

The computational complexity of this approach is O(N^2 * 2^N) which is discussed later in this article.

The nearest neighbor method is a heuristic-based greedy approach where we choose the nearest neighbor node. This approach is computationally less expensive than the dynamic approach. But it does not provide the guarantee of an optimal solution. This method is used for near-optimal solutions.

Algorithm for Traveling Salesman Problem

We will use the dynamic programming approach to solve the Travelling Salesman Problem (TSP).

Before starting the algorithm, let’s get acquainted with some terminologies:

• A graph G=(V, E), which is a set of vertices and edges.
• V is the set of vertices.
• E is the set of edges.
• Vertices are connected through edges.
• Dist(i,j) denotes the non-negative distance between two vertices, i and j.

Let’s assume S is the subset of cities and belongs to {1, 2, 3, …, n} where 1, 2, 3…n are the cities and i, j are two cities in that subset. Now cost(i, S, j) is defined in such a way as the length of the shortest path visiting node in S, which is exactly once having the starting and ending point as i and j respectively.

For example, cost (1, {2, 3, 4}, 1) denotes the length of the shortest path where:

• Starting city is 1
• Cities 2, 3, and 4 are visited only once
• The ending point is 1

The dynamic programming algorithm would be:

• Set cost(i, , i) = 0, which means we start and end at i, and the cost is 0.
• When |S| > 1, we define cost(i, S, 1) = ∝ where i !=1 . Because initially, we do not know the exact cost to reach city i to city 1 through other cities.
• Now, we need to start at 1 and complete the tour. We need to select the next city in such a way-

cost(i, S, j)=min cost (i, S−{i}, j)+dist(i,j) where i∈S and i≠j

For the given figure, the adjacency matrix would be the following:

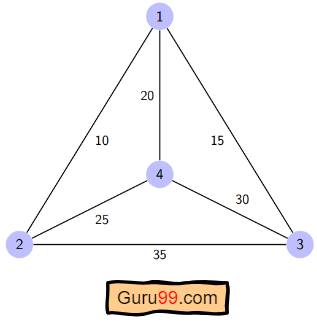
Let’s see how our algorithm works:

Step 1) We are considering our journey starting at city 1, visit other cities once and return to city 1.

Step 2) S is the subset of cities. According to our algorithm, for all |S| > 1, we will set the distance cost(i, S, 1) = ∝. Here cost(i, S, j) means we are starting at city i, visiting the cities of S once, and now we are at city j. We set this path cost as infinity because we do not know the distance yet. So the values will be the following:

Cost (2, {3, 4}, 1) = ∝ ; the notation denotes we are starting at city 2, going through cities 3, 4, and reaching 1. And the path cost is infinity. Similarly-

cost(3, {2, 4}, 1) = ∝

cost(4, {2, 3}, 1) = ∝

Step 3) Now, for all subsets of S, we need to find the following:

cost(i, S, j)=min cost (i, S−{i}, j)+dist(i,j), where j∈S and i≠j

That means the minimum cost path for starting at i, going through the subset of cities once, and returning to city j. Considering that the journey starts at city 1, the optimal path cost would be= cost(1, {other cities}, 1).

Let’s find out how we could achieve that:

Now S = {1, 2, 3, 4}. There are four elements. Hence the number of subsets will be 2^4 or 16. Those subsets are-

1) |S| = Null:

2) |S| = 1:

{{1}, {2}, {3}, {4}}

3) |S| = 2:

{{1, 2}, {1, 3}, {1, 4}, {2, 3}, {2, 4}, {3, 4}}

4) |S| = 3:

{{1, 2, 3}, {1, 2, 4}, {2, 3, 4}, {1, 3, 4}}

5) |S| = 4:

{{1, 2, 3, 4}}

As we are starting at 1, we could discard the subsets containing city 1.

The algorithm calculation:

1) |S| = Φ:

cost (2, Φ, 1) = dist(2, 1) = 10

cost (3, Φ, 1) = dist(3, 1) = 15

cost (4, Φ, 1) = dist(4, 1) = 20

cost (2, {3}, 1) = dist(2, 3) + cost (3, Φ, 1) = 35+15 = 50

cost (2, {4}, 1) = dist(2, 4) + cost (4, Φ, 1) = 25+20 = 45

cost (3, {2}, 1) = dist(3, 2) + cost (2, Φ, 1) = 35+10 = 45

cost (3, {4}, 1) = dist(3, 4) + cost (4, Φ, 1) = 30+20 = 50

cost (4, {2}, 1) = dist(4, 2) + cost (2, Φ, 1) = 25+10 = 35

cost (4, {3}, 1) = dist(4, 3) + cost (3, Φ, 1) = 30+15 = 45

cost (2, {3, 4}, 1) = min [ dist[2,3]+Cost(3,{4},1) = 35+50 = 85,

dist[2,4]+Cost(4,{3},1) = 25+45 = 70 ] = 70

cost (3, {2, 4}, 1) = min [ dist[3,2]+Cost(2,{4},1) = 35+45 = 80,

dist[3,4]+Cost(4,{2},1) = 30+35 = 65 ] = 65

cost (4, {2, 3}, 1) = min [ dist[4,2]+Cost(2,{3},1) = 25+50 = 75

dist[4,3]+Cost(3,{2},1) = 30+45 = 75 ] = 75

cost (1, {2, 3, 4}, 1) = min [ dist[1,2]+Cost(2,{3,4},1) = 10+70 = 80

dist[1,3]+Cost(3,{2,4},1) = 15+65 = 80

dist[1,4]+Cost(4,{2,3},1) = 20+75 = 95 ] = 80

So the optimal solution would be 1-2-4-3-1

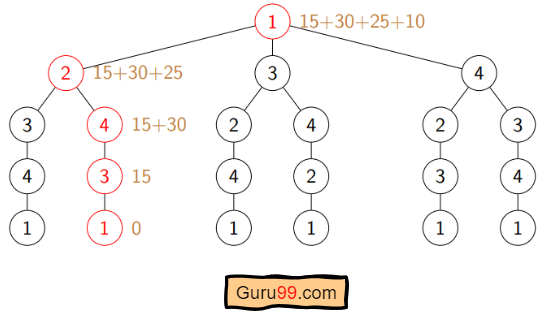
Pseudo-code

Implementation in c/c++.

Here’s the implementation in C++ :

Implementation in Python

Academic solutions to tsp.

Computer scientists have spent years searching for an improved polynomial time algorithm for the Travelling Salesman Problem. Until now, the problem is still NP-hard.

Though some of the following solutions were published in recent years that have reduced the complexity to a certain degree:

• The classical symmetric TSP is solved by the Zero Suffix Method.
• The Biogeography‐based Optimization Algorithm is based on the migration strategy to solve the optimization problems that can be planned as TSP.
• Multi-Objective Evolutionary Algorithm is designed for solving multiple TSP based on NSGA-II.
• The Multi-Agent System solves the TSP of N cities with fixed resources.

Application of Traveling Salesman Problem

Travelling Salesman Problem (TSP) is applied in the real world in both its purest and modified forms. Some of those are:

• Planning, logistics, and manufacturing microchips : Chip insertion problems naturally arise in the microchip industry. Those problems can be planned as traveling salesman problems.
• DNA sequencing : Slight modification of the traveling salesman problem can be used in DNA sequencing. Here, the cities represent the DNA fragments, and the distance represents the similarity measure between two DNA fragments.
• Astronomy : The Travelling Salesman Problem is applied by astronomers to minimize the time spent observing various sources.
• Optimal control problem : Travelling Salesman Problem formulation can be applied in optimal control problems. There might be several other constraints added.

Complexity Analysis of TSP

So the total time complexity for an optimal solution would be the Number of nodes * Number of subproblems * time to solve each sub-problem. The time complexity can be defined as O(N 2 * 2^N).

• Space Complexity: The dynamic programming approach uses memory to store C(S, i), where S is a subset of the vertices set. There is a total of 2 N subsets for each node. So, the space complexity is O(2^N).

Next, you’ll learn about Sieve of Eratosthenes Algorithm

• Linear Search: Python, C++ Example
• DAA Tutorial PDF: Design and Analysis of Algorithms
• Heap Sort Algorithm (With Code in Python and C++)
• Kadence’s Algorithm: Largest Sum Contiguous Subarray
• Radix Sort Algorithm in Data Structure
• Doubly Linked List: C++, Python (Code Example)
• Singly Linked List in Data Structures
• Adjacency List and Matrix Representation of Graph