travelling salesman problem w3schools

DSA Tutorial

Linked lists, stacks & queues, hash tables, shortest path, minimum spanning tree, maximum flow, time complexity, dsa reference, dsa examples, dsa the traveling salesman problem.

The Traveling Salesman Problem

The Traveling Salesman Problem states that you are a salesperson and you must visit a number of cities or towns.

Rules : Visit every city only once, then return back to the city you started in.

Goal : Find the shortest possible route.

Except for the Held-Karp algorithm (which is quite advanced and time consuming, (\(O(2^n n^2)\)), and will not be described here), there is no other way to find the shortest route than to check all possible routes.

This means that the time complexity for solving this problem is \(O(n!)\), which means 720 routes needs to be checked for 6 cities, 40,320 routes must be checked for 8 cities, and if you have 10 cities to visit, more than 3.6 million routes must be checked!

Note: "!", or "factorial", is a mathematical operation used in combinatorics to find out how many possible ways something can be done. If there are 4 cities, each city is connected to every other city, and we must visit every city exactly once, there are \(4!= 4 \cdot 3 \cdot 2 \cdot 1 = 24\) different routes we can take to visit those cities.

The Traveling Salesman Problem (TSP) is a problem that is interesting to study because it is very practical, but so time consuming to solve, that it becomes nearly impossible to find the shortest route, even in a graph with just 20-30 vertices.

If we had an effective algorithm for solving The Traveling Salesman Problem, the consequences would be very big in many sectors, like for example chip design, vehicle routing, telecommunications, and urban planning.

Checking All Routes to Solve The Traveling Salesman Problem

To find the optimal solution to The Traveling Salesman Problem, we will check all possible routes, and every time we find a shorter route, we will store it, so that in the end we will have the shortest route.

Good: Finds the overall shortest route.

Bad: Requires an awful lot of calculation, especially for a large amount of cities, which means it is very time consuming.

How it works:

• Check the length of every possible route, one route at a time.
• Is the current route shorter than the shortest route found so far? If so, store the new shortest route.
• After checking all routes, the stored route is the shortest one.

Such a way of finding the solution to a problem is called brute force .

Brute force is not really an algorithm, it just means finding the solution by checking all possibilities, usually because of a lack of a better way to do it.

Speed: {{ inpVal }}

Finding the shortest route in The Traveling Salesman Problem by checking all routes (brute force).

Progress: {{progress}}%

n = {{vertices}} cities

{{vertices}}!={{posRoutes}} possible routes

Show every route: {{showCompares}}

The reason why the brute force approach of finding the shortest route (as shown above) is so time consuming is that we are checking all routes, and the number of possible routes increases really fast when the number of cities increases.

Finding the optimal solution to the Traveling Salesman Problem by checking all possible routes (brute force):

Using A Greedy Algorithm to Solve The Traveling Salesman Problem

Since checking every possible route to solve the Traveling Salesman Problem (like we did above) is so incredibly time consuming, we can instead find a short route by just going to the nearest unvisited city in each step, which is much faster.

Good: Finds a solution to the Traveling Salesman Problem much faster than by checking all routes.

Bad: Does not find the overall shortest route, it just finds a route that is much shorter than an average random route.

• Visit every city.
• The next city to visit is always the nearest of the unvisited cities from the city you are currently in.
• After visiting all cities, go back to the city you started in.

This way of finding an approximation to the shortest route in the Traveling Salesman Problem, by just going to the nearest unvisited city in each step, is called a greedy algorithm .

Finding an approximation to the shortest route in The Traveling Salesman Problem by always going to the nearest unvisited neighbor (greedy algorithm).

As you can see by running this simulation a few times, the routes that are found are not completely unreasonable. Except for a few times when the lines cross perhaps, especially towards the end of the algorithm, the resulting route is a lot shorter than we would get by choosing the next city at random.

Finding a near-optimal solution to the Traveling Salesman Problem using the nearest-neighbor algorithm (greedy):

Other Algorithms That Find Near-Optimal Solutions to The Traveling Salesman Problem

In addition to using a greedy algorithm to solve the Traveling Salesman Problem, there are also other algorithms that can find approximations to the shortest route.

These algorithms are popular because they are much more effective than to actually check all possible solutions, but as with the greedy algorithm above, they do not find the overall shortest route.

Algorithms used to find a near-optimal solution to the Traveling Salesman Problem include:

• 2-opt Heuristic: An algorithm that improves the solution step-by-step, in each step removing two edges and reconnecting the two paths in a different way to reduce the total path length.
• Genetic Algorithm: This is a type of algorithm inspired by the process of natural selection and use techniques such as selection, mutation, and crossover to evolve solutions to problems, including the TSP.
• Simulated Annealing: This method is inspired by the process of annealing in metallurgy. It involves heating and then slowly cooling a material to decrease defects. In the context of TSP, it's used to find a near-optimal solution by exploring the solution space in a way that allows for occasional moves to worse solutions, which helps to avoid getting stuck in local minima.
• Ant Colony Optimization: This algorithm is inspired by the behavior of ants in finding paths from the colony to food sources. It's a more complex probabilistic technique for solving computational problems which can be mapped to finding good paths through graphs.

Time Complexity for Solving The Traveling Salesman Problem

To get a near-optimal solution fast, we can use a greedy algorithm that just goes to the nearest unvisited city in each step, like in the second simulation on this page.

Solving The Traveling Salesman Problem in a greedy way like that, means that at each step, the distances from the current city to all other unvisited cities are compared, and that gives us a time complexity of \(O(n^2) \).

But finding the shortest route of them all requires a lot more operations, and the time complexity for that is \(O(n!)\), like mentioned earlier, which means that for 4 cities, there are 4! possible routes, which is the same as \(4 \cdot 3 \cdot 2 \cdot 1 = 24\). And for just 12 cities for example, there are \(12! = 12 \cdot 11 \cdot 10 \cdot \; ... \; \cdot 2 \cdot 1 = 479,001,600\) possible routes!

See the time complexity for the greedy algorithm \(O(n^2)\), versus the time complexity for finding the shortest route by comparing all routes \(O(n!)\), in the image below.

But there are two things we can do to reduce the number of routes we need to check.

In the Traveling Salesman Problem, the route starts and ends in the same place, which makes a cycle. This means that the length of the shortest route will be the same no matter which city we start in. That is why we have chosen a fixed city to start in for the simulation above, and that reduces the number of possible routes from \(n!\) to \((n-1)!\).

Also, because these routes go in cycles, a route has the same distance if we go in one direction or the other, so we actually just need to check the distance of half of the routes, because the other half will just be the same routes in the opposite direction, so the number of routes we need to check is actually \( \frac{(n-1)!}{2}\).

But even if we can reduce the number of routes we need to check to \( \frac{(n-1)!}{2}\), the time complexity is still \( O(n!)\), because for very big \(n\), reducing \(n\) by one and dividing by 2 does not make a significant change in how the time complexity grows when \(n\) is increased.

To better understand how time complexity works, go to this page .

Actual Traveling Salesman Problems Are More Complex

The edge weight in a graph in this context of The Traveling Salesman Problem tells us how hard it is to go from one point to another, and it is the total edge weight of a route we want to minimize.

So far on this page, the edge weight has been the distance in a straight line between two points. And that makes it much easier to explain the Traveling Salesman Problem, and to display it.

But in the real world there are many other things that affects the edge weight:

• Obstacles: When moving from one place to another, we normally try to avoid obstacles like trees, rivers, houses for example. This means it is longer and takes more time to go from A to B, and the edge weight value needs to be increased to factor that in, because it is not a straight line anymore.
• Transportation Networks: We usually follow a road or use public transport systems when traveling, and that also affects how hard it is to go (or send a package) from one place to another.
• Traffic Conditions: Travel congestion also affects the travel time, so that should also be reflected in the edge weight value.
• Legal and Political Boundaries: Crossing border for example, might make one route harder to choose than another, which means the shortest straight line route might be slower, or more costly.
• Economic Factors: Using fuel, using the time of employees, maintaining vehicles, all these things cost money and should also be factored into the edge weights.

As you can see, just using the straight line distances as the edge weights, might be too simple compared to the real problem. And solving the Traveling Salesman Problem for such a simplified problem model would probably give us a solution that is not optimal in a practical sense.

It is not easy to visualize a Traveling Salesman Problem when the edge length is not just the straight line distance between two points anymore, but the computer handles that very well.

COLOR PICKER

Report Error

If you want to report an error, or if you want to make a suggestion, do not hesitate to send us an e-mail:

[email protected]

Top Tutorials

Top references, top examples, get certified.

Forgot password? New user? Sign up

Existing user? Log in

Traveling Salesperson Problem

Already have an account? Log in here.

A salesperson needs to visit a set of cities to sell their goods. They know how many cities they need to go to and the distances between each city. In what order should the salesperson visit each city exactly once so that they minimize their travel time and so that they end their journey in their city of origin?

The traveling salesperson problem is an extremely old problem in computer science that is an extension of the Hamiltonian Circuit Problem . It has important implications in complexity theory and the P versus NP problem because it is an NP-Complete problem . This means that a solution to this problem cannot be found in polynomial time (it takes superpolynomial time to compute an answer). In other words, as the number of vertices increases linearly, the computation time to solve the problem increases exponentially.

The following image is a simple example of a network of cities connected by edges of a specific distance. The origin city is also marked.

Network of cities

Here is the solution for that network, it has a distance traveled of only 14. Any other path that the salesman can takes will result in a path length that is more than 14.

Relationship to Graphs

Special kinds of tsp, importance for p vs np, applications.

The traveling salesperson problem can be modeled as a graph . Specifically, it is typical a directed, weighted graph. Each city acts as a vertex and each path between cities is an edge. Instead of distances, each edge has a weight associated with it. In this model, the goal of the traveling salesperson problem can be defined as finding a path that visits every vertex, returns to the original vertex, and minimizes total weight.

To that end, many graph algorithms can be used on this model. Search algorithms like breadth-first search (BFS) , depth-first search (DFS) , and Dijkstra's shortest path algorithm can certainly be used, however, they do not take into consideration that fact that every vertex must be visited.

The Traveling Salesperson Problem (TSP), an NP-Complete problem, is notoriously complicated to solve. That is because the greedy approach is so computational intensive. The greedy approach to solving this problem would be to try every single possible path and see which one is the fastest. Try this conceptual question to see if you have a grasp for how hard it is to solve.

For a fully connected map with \(n\) cities, how many total paths are possible for the traveling salesperson? Show Answer There are (n-1)! total paths the salesperson can take. The computation needed to solve this problem in this way grows far too quickly to be a reasonable solution. If this map has only 5 cities, there are \(4!\), or 24, paths. However, if the size of this map is increased to 20 cities, there will be \(1.22 \cdot 10^{17}\) paths!

The greedy approach to TSP would go like this:

• Find all possible paths.
• Find the cost of every paths.
• Choose the path with the lowest cost.

Another version of a greedy approach might be: At every step in the algorithm, choose the best possible path. This version might go a little quicker, but it's not guaranteed to find the best answer, or an answer at all since it might hit a dead end.

For NP-Hard problems (a subset of NP-Complete problems) like TSP, exact solutions can only be implemented in a reasonable amount of time for small input sizes (maps with few cities). Otherwise, the best approach we can do is provide a heuristic to help the problem move forward in an optimal way. However, these approaches cannot be proven to be optimal because they always have some sort of downside.

Small input sizes

As described, in a previous section , the greedy approach to this problem has a complexity of \(O(n!)\). However, there are some approaches that decrease this computation time.

The Held-Karp Algorithm is one of the earliest applications of dynamic programming . Its complexity is much lower than the greedy approach at \(O(n^2 2^n)\). Basically what this algorithm says is that every sub path along an optimal path is itself an optimal path. So, computing an optimal path is the same as computing many smaller subpaths and adding them together.

Heuristics are a way of ranking possible next steps in an algorithm in the hopes of cutting down computation time for the entire algorithm. They are often a tradeoff of some attribute - such as completeness, accuracy, or precision - in favor of speed. Heuristics exist for the traveling salesperson problem as well.

The most simple heuristic for this problem is the greedy heuristic. This heuristic simply says, at each step of the network traversal, choose the best next step. In other words, always choose the closest city that you have not yet visited. This heuristic seems like a good one because it is simple and intuitive, and it is even used in practice sometimes, however there are heuristics that are proven to be more effective.

Christofides algorithm is another heuristic. It produces at most 1.5 times the optimal weight for TSP. This algorithm involves finding a minimum spanning tree for the network. Next, it creates matchings for the cities of an odd degree (meaning they have an odd number of edges coming out of them), calculates an eulerian path , and converts back to a TSP path.

Even though it is typically impossible to optimally solve TSP problems, there are cases of TSP problems that can be solved if certain conditions hold.

The metric-TSP is an instance of TSP that satisfies this condition: The distance from city A to city B is less than or equal to the distance from city A to city C plus the distance from city C to city B. Or,

\[distance_{AB} \leq distance_{AC} + distance_{CB}\]

This is a condition that holds in the real world, but it can't always be expected to hold for every TSP problem. But, with this inequality in place, the approximated path will be no more than twice the optimal path. Even better, we can bound the solution to a \(3/2\) approximation by using Christofide's Algorithm .

The euclidean-TSP has an even stricter constraint on the TSP input. It states that all cities' edges in the network must obey euclidean distances . Recent advances have shown that approximation algorithms using euclidean minimum spanning trees have reduced the runtime of euclidean-TSP, even though they are also NP-hard. In practice, though, simpler heuristics are still used.

The P versus NP problem is one of the leading questions in modern computer science. It asks whether or not every problem whose solution can be verified in polynomial time by a computer can also be solved in polynomial time by a computer. TSP, for example, cannot be solved in polynomial time (at least that's what is currently theorized). However, TSP can be solved in polynomial time when it is phrased like this: Given a graph and an integer, x, decide if there is a path of length x or less than x . It's easy to see that given a proposed answer to this question, it is simple to check if it is less than or equal to x.

The traveling salesperson problem, like other problems that are NP-Complete, are very important to this debate. That is because if a polynomial time solution can be found to this problems, then \(P = NP\). As it stands, most scientists believe that \(P \ne NP\).

The traveling salesperson problem has many applications. The obvious ones are in the transportation space. Planning delivery routes or flight patterns, for example, would benefit immensly from breakthroughs is this problem or in the P versus NP problem .

However, this same logic can be applied to many facets of planning as well. In robotics, for instance, planning the order in which to drill holes in a circuit board is a complex task due to the sheer number of holes that must be drawn.

The best and most important application of TSP, however, comes from the fact that it is an NP-Complete problem. That means that its practical applications amount to the applications of any problem that is NP-Complete. So, if there are significant breakthroughs for TSP, that means that those exact same breakthrough can be applied to any problem in the NP-Complete class.

Problem Loading...

Note Loading...

Set Loading...

• Interview Q

DAA Tutorial

Asymptotic analysis, analysis of sorting, divide and conquer, lower bound theory, sorting in linear time, binary search trees, red black tree, dynamic programming, greedy algorithm, backtracking, shortest path, all-pairs shortest paths, maximum flow, sorting networks, complexity theory, approximation algo, string matching.

Interview Questions

• Send your Feedback to [email protected]

Help Others, Please Share

Learn Latest Tutorials

Transact-SQL

Reinforcement Learning

R Programming

React Native

Python Design Patterns

Python Pillow

Python Turtle

Preparation

Verbal Ability

Company Questions

Trending Technologies

Artificial Intelligence

Cloud Computing

Data Science

Machine Learning

B.Tech / MCA

Data Structures

Operating System

Computer Network

Compiler Design

Computer Organization

Discrete Mathematics

Ethical Hacking

Computer Graphics

Software Engineering

Web Technology

Cyber Security

C Programming

Control System

Data Mining

Data Warehouse

Traveling salesman problem

This web page is a duplicate of https://optimization.mccormick.northwestern.edu/index.php/Traveling_salesman_problems

Author: Jessica Yu (ChE 345 Spring 2014)

Steward: Dajun Yue, Fengqi You

The traveling salesman problem (TSP) is a widely studied combinatorial optimization problem, which, given a set of cities and a cost to travel from one city to another, seeks to identify the tour that will allow a salesman to visit each city only once, starting and ending in the same city, at the minimum cost. 1

• 2.1 Graph Theory
• 2.2 Classifications of the TSP
• 2.3 Variations of the TSP
• 3.1 aTSP ILP Formulation
• 3.2 sTSP ILP Formulation
• 4.1 Exact algorithms
• 4.2.1 Tour construction procedures
• 4.2.2 Tour improvement procedures
• 5 Applications
• 7 References

The origins of the traveling salesman problem are obscure; it is mentioned in an 1832 manual for traveling salesman, which included example tours of 45 German cities but gave no mathematical consideration. 2 W. R. Hamilton and Thomas Kirkman devised mathematical formulations of the problem in the 1800s. 2

It is believed that the general form was first studied by Karl Menger in Vienna and Harvard in the 1930s. 2,3

Hassler Whitney, who was working on his Ph.D. research at Harvard when Menger was a visiting lecturer, is believed to have posed the problem of finding the shortest route between the 48 states of the United States during either his 1931-1932 or 1934 seminar talks. 2 There is also uncertainty surrounding the individual who coined the name “traveling salesman problem” for Whitney’s problem. 2

The problem became increasingly popular in the 1950s and 1960s. Notably, George Dantzig, Delber R. Fulkerson, and Selmer M. Johnson at the RAND Corporation in Santa Monica, California solved the 48 state problem by formulating it as a linear programming problem. 2 The methods described in the paper set the foundation for future work in combinatorial optimization, especially highlighting the importance of cutting planes. 2,4

In the early 1970s, the concept of P vs. NP problems created buzz in the theoretical computer science community. In 1972, Richard Karp demonstrated that the Hamiltonian cycle problem was NP-complete, implying that the traveling salesman problem was NP-hard. 4

Increasingly sophisticated codes led to rapid increases in the sizes of the traveling salesman problems solved. Dantzig, Fulkerson, and Johnson had solved a 48 city instance of the problem in 1954. 5 Martin Grötechel more than doubled this 23 years later, solving a 120 city instance in 1977. 5 Enoch Crowder and Manfred W. Padberg again more than doubled this in just 3 years, with a 318 city solution. 5

In 1987, rapid improvements were made, culminating in a 2,392 city solution by Padberg and Giovanni Rinaldi. In the following two decades, David L. Appelgate, Robert E. Bixby, Vasek Chvátal, & William J. Cook led the cutting edge, solving a 7,397 city instance in 1994 up to the current largest solved problem of 24,978 cities in 2004. 5

Description

Graph theory.

In the context of the traveling salesman problem, the verticies correspond to cities and the edges correspond to the path between those cities. When modeled as a complete graph, paths that do not exist between cities can be modeled as edges of very large cost without loss of generality. 6 Minimizing the sum of the costs for Hamiltonian cycle is equivalent to identifying the shortest path in which each city is visiting only once.

Classifications of the TSP

The TRP can be divided into two classes depending on the nature of the cost matrix. 3,6

• Applies when the distance between cities is the same in both directions

• Applies when there are differences in distances (e.g. one-way streets)

An ATSP can be formulated as an STSP by doubling the number of nodes. 6

Variations of the TSP

Formulation

The objective function is then given by

To ensure that the result is a valid tour, several contraints must be added. 1,3

There are several other formulations for the subtour elimnation contraint, including circuit packing contraints, MTZ constraints, and network flow constraints.

aTSP ILP Formulation

The integer linear programming formulation for an aTSP is given by

sTSP ILP Formulation

The symmetric case is a special case of the asymmetric case and the above formulation is valid. 3, 6 The integer linear programming formulation for an sTSP is given by

Exact algorithms

Branch-and-bound algorithms are commonly used to find solutions for TSPs. 7 The ILP is first relaxed and solved as an LP using the Simplex method, then feasibility is regained by enumeration of the integer variables. 7

Other exact solution methods include the cutting plane method and branch-and-cut. 8

Heuristic algorithms

Given that the TSP is an NP-hard problem, heuristic algorithms are commonly used to give a approximate solutions that are good, though not necessarily optimal. The algorithms do not guarantee an optimal solution, but gives near-optimal solutions in reasonable computational time. 3 The Held-Karp lower bound can be calculated and used to judge the performance of a heuristic algorithm. 3

There are two general heuristic classifications 7 :

• Tour construction procedures where a solution is gradually built by adding a new vertex at each step
• Tour improvement procedures where a feasbile solution is improved upon by performing various exchanges

The best methods tend to be composite algorithms that combine these features. 7

Tour construction procedures

Tour improvement procedures

Applications

The importance of the traveling salesman problem is two fold. First its ubiquity as a platform for the study of general methods than can then be applied to a variety of other discrete optimization problems. 5 Second is its diverse range of applications, in fields including mathematics, computer science, genetics, and engineering. 5,6

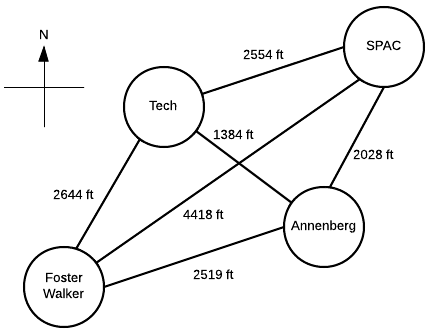
Suppose a Northwestern student, who lives in Foster-Walker , has to accomplish the following tasks:

• Drop off a homework set at Tech
• Work out a SPAC
• Complete a group project at Annenberg

Distances between buildings can be found using Google Maps. Note that there is particularly strong western wind and walking east takes 1.5 times as long.

It is the middle of winter and the student wants to spend the least possible time walking. Determine the path the student should take in order to minimize walking time, starting and ending at Foster-Walker.

Start with the cost matrix (with altered distances taken into account):

Method 1: Complete Enumeration

All possible paths are considered and the path of least cost is the optimal solution. Note that this method is only feasible given the small size of the problem.

From inspection, we see that Path 4 is the shortest. So, the student should walk 2.28 miles in the following order: Foster-Walker → Annenberg → SPAC → Tech → Foster-Walker

Method 2: Nearest neighbor

Starting from Foster-Walker, the next building is simply the closest building that has not yet been visited. With only four nodes, this can be done by inspection:

• Smallest distance is from Foster-Walker is to Annenberg
• Smallest distance from Annenberg is to Tech
• Smallest distance from Tech is to Annenberg ( creates a subtour, therefore skip )
• Next smallest distance from Tech is to Foster-Walker ( creates a subtour, therefore skip )
• Next smallest distance from Tech is to SPAC
• Smallest distance from SPAC is to Annenberg ( creates a subtour, therefore skip )
• Next smallest distance from SPAC is to Tech ( creates a subtour, therefore skip )
• Next smallest distance from SPAC is to Foster-Walker

So, the student would walk 2.54 miles in the following order: Foster-Walker → Annenberg → Tech → SPAC → Foster-Walker

Method 3: Greedy

With this method, the shortest paths that do not create a subtour are selected until a complete tour is created.

• Smallest distance is Annenberg → Tech
• Next smallest is SPAC → Annenberg
• Next smallest is Tech → Annenberg ( creates a subtour, therefore skip )
• Next smallest is Anneberg → Foster-Walker ( creates a subtour, therefore skip )
• Next smallest is SPAC → Tech ( creates a subtour, therefore skip )
• Next smallest is Tech → Foster-Walker
• Next smallest is Annenberg → SPAC ( creates a subtour, therefore skip )
• Next smallest is Foster-Walker → Annenberg ( creates a subtour, therefore skip )
• Next smallest is Tech → SPAC ( creates a subtour, therefore skip )
• Next smallest is Foster-Walker → Tech ( creates a subtour, therefore skip )
• Next smallest is SPAC → Foster-Walker ( creates a subtour, therefore skip )
• Next smallest is Foster-Walker → SPAC

So, the student would walk 2.40 miles in the following order: Foster-Walker → SPAC → Annenberg → Tech → Foster-Walker

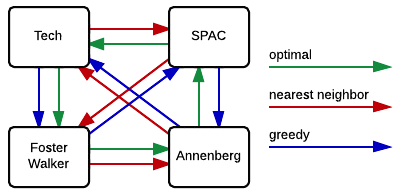
As we can see in the figure to the right, the heuristic methods did not give the optimal solution. That is not to say that heuristics can never give the optimal solution, just that it is not guaranteed.

Both the optimal and the nearest neighbor algorithms suggest that Annenberg is the optimal first building to visit. However, the optimal solution then goes to SPAC, while both heuristic methods suggest Tech. This is in part due to the large cost of SPAC → Foster-Walker. The heuristic algorithms cannot take this future cost into account, and therefore fall into that local optimum.

We note that the nearest neighbor and greedy algorithms give solutions that are 11.4% and 5.3%, respectively, above the optimal solution. In the scale of this problem, this corresponds to fractions of a mile. We also note that neither heuristic gave the worst case result, Foster-Walker → SPAC → Tech → Annenberg → Foster-Walker.

Only tour building heuristics were used. Combined with a tour improvement algorithm (such as 2-opt or simulated annealing), we imagine that we may be able to locate solutions that are closer to the optimum.

The exact algorithm used was complete enumeration, but we note that this is impractical even for 7 nodes (6! or 720 different possibilities). Commonly, the problem would be formulated and solved as an ILP to obtain exact solutions.

• Vanderbei, R. J. (2001). Linear programming: Foundations and extensions (2nd ed.). Boston: Kluwer Academic.
• Schrijver, A. (n.d.). On the history of combinatorial optimization (till 1960).
• Matai, R., Singh, S., & Lal, M. (2010). Traveling salesman problem: An overview of applications, formulations, and solution approaches. In D. Davendra (Ed.), Traveling Salesman Problem, Theory and Applications . InTech.
• Junger, M., Liebling, T., Naddef, D., Nemhauser, G., Pulleyblank, W., Reinelt, G., Rinaldi, G., & Wolsey, L. (Eds.). (2009). 50 years of integer programming, 1958-2008: The early years and state-of-the-art surveys . Heidelberg: Springer.
• Cook, W. (2007). History of the TSP. The Traveling Salesman Problem . Retrieved from http://www.math.uwaterloo.ca/tsp/history/index.htm
• Punnen, A. P. (2002). The traveling salesman problem: Applications, formulations and variations. In G. Gutin & A. P. Punnen (Eds.), The Traveling Salesman Problem and its Variations . Netherlands: Kluwer Academic Publishers.
• Laporte, G. (1992). The traveling salesman problem: An overview of exact and approximate algorithms. European Journal of Operational Research, 59 (2), 231–247.
• Goyal, S. (n.d.). A suvey on travlling salesman problem.

Navigation menu

• Data Structures & Algorithms
• DSA - Overview
• DSA - Environment Setup
• DSA - Algorithms Basics
• DSA - Asymptotic Analysis
• Data Structures
• DSA - Data Structure Basics
• DSA - Data Structures and Types
• DSA - Array Data Structure
• Linked Lists
• DSA - Linked List Data Structure
• DSA - Doubly Linked List Data Structure
• DSA - Circular Linked List Data Structure
• Stack & Queue
• DSA - Stack Data Structure
• DSA - Expression Parsing
• DSA - Queue Data Structure
• Searching Algorithms
• DSA - Searching Algorithms
• DSA - Linear Search Algorithm
• DSA - Binary Search Algorithm
• DSA - Interpolation Search
• DSA - Jump Search Algorithm
• DSA - Exponential Search
• DSA - Fibonacci Search
• DSA - Sublist Search
• DSA - Hash Table
• Sorting Algorithms
• DSA - Sorting Algorithms
• DSA - Bubble Sort Algorithm
• DSA - Insertion Sort Algorithm
• DSA - Selection Sort Algorithm
• DSA - Merge Sort Algorithm
• DSA - Shell Sort Algorithm
• DSA - Heap Sort
• DSA - Bucket Sort Algorithm
• DSA - Counting Sort Algorithm
• DSA - Radix Sort Algorithm
• DSA - Quick Sort Algorithm
• Graph Data Structure
• DSA - Graph Data Structure
• DSA - Depth First Traversal
• DSA - Breadth First Traversal
• DSA - Spanning Tree
• Tree Data Structure
• DSA - Tree Data Structure
• DSA - Tree Traversal
• DSA - Binary Search Tree
• DSA - AVL Tree
• DSA - Red Black Trees
• DSA - B Trees
• DSA - B+ Trees
• DSA - Splay Trees
• DSA - Tries
• DSA - Heap Data Structure
• DSA - Recursion Algorithms
• DSA - Tower of Hanoi Using Recursion
• DSA - Fibonacci Series Using Recursion
• Divide and Conquer
• DSA - Divide and Conquer
• DSA - Max-Min Problem
• DSA - Strassen's Matrix Multiplication
• DSA - Karatsuba Algorithm
• Greedy Algorithms
• DSA - Greedy Algorithms
• DSA - Travelling Salesman Problem (Greedy Approach)
• DSA - Prim's Minimal Spanning Tree
• DSA - Kruskal's Minimal Spanning Tree
• DSA - Dijkstra's Shortest Path Algorithm
• DSA - Map Colouring Algorithm
• DSA - Fractional Knapsack Problem
• DSA - Job Sequencing with Deadline
• DSA - Optimal Merge Pattern Algorithm
• Dynamic Programming
• DSA - Dynamic Programming
• DSA - Matrix Chain Multiplication
• DSA - Floyd Warshall Algorithm
• DSA - 0-1 Knapsack Problem
• DSA - Longest Common Subsequence Algorithm
• DSA - Travelling Salesman Problem (Dynamic Approach)
• Approximation Algorithms
• DSA - Approximation Algorithms
• DSA - Vertex Cover Algorithm
• DSA - Set Cover Problem
• DSA - Travelling Salesman Problem (Approximation Approach)
• Randomized Algorithms
• DSA - Randomized Algorithms
• DSA - Randomized Quick Sort Algorithm
• DSA - Karger’s Minimum Cut Algorithm
• DSA - Fisher-Yates Shuffle Algorithm
• DSA Useful Resources
• DSA - Questions and Answers
• DSA - Quick Guide
• DSA - Useful Resources
• DSA - Discussion
• Selected Reading
• UPSC IAS Exams Notes
• Developer's Best Practices
• Questions and Answers
• Effective Resume Writing
• HR Interview Questions
• Computer Glossary

Travelling Salesman Problem (Dynamic Approach)

Travelling salesman dynamic programming algorithm, implementation.

Travelling salesman problem is the most notorious computational problem. We can use brute-force approach to evaluate every possible tour and select the best one. For n number of vertices in a graph, there are (n−1)! number of possibilities. Thus, maintaining a higher complexity.

However, instead of using brute-force, using the dynamic programming approach will obtain the solution in lesser time, though there is no polynomial time algorithm.

Let us consider a graph G = (V,E) , where V is a set of cities and E is a set of weighted edges. An edge e(u, v) represents that vertices u and v are connected. Distance between vertex u and v is d(u, v) , which should be non-negative.

Suppose we have started at city 1 and after visiting some cities now we are in city j . Hence, this is a partial tour. We certainly need to know j , since this will determine which cities are most convenient to visit next. We also need to know all the cities visited so far, so that we don't repeat any of them. Hence, this is an appropriate sub-problem.

For a subset of cities S $\epsilon$ {1,2,3,...,n} that includes 1 , and j $\epsilon$ S, let C(S, j) be the length of the shortest path visiting each node in S exactly once, starting at 1 and ending at j .

When |S|> 1 , we define 𝑪 C(S,1)= $\propto$ since the path cannot start and end at 1.

Now, let express C(S, j) in terms of smaller sub-problems. We need to start at 1 and end at j . We should select the next city in such a way that

$$C\left ( S,j \right )\, =\, min\, C\left ( S\, -\, \left\{j \right\},i \right )\, +\, d\left ( i,j \right )\: where\: i\: \epsilon \: S\: and\: i\neq j$$

There are at the most 2 n .n sub-problems and each one takes linear time to solve. Therefore, the total running time is O(2 n .n 2 ) .

In the following example, we will illustrate the steps to solve the travelling salesman problem.

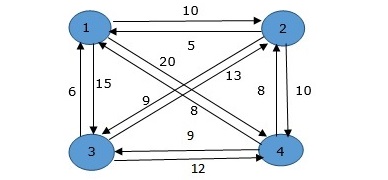
From the above graph, the following table is prepared.

$$Cost\left ( 2,\Phi ,1 \right )\, =\, d\left ( 2,1 \right )\,=\,5$$

$$Cost\left ( 3,\Phi ,1 \right )\, =\, d\left ( 3,1 \right )\, =\, 6$$

$$Cost\left ( 4,\Phi ,1 \right )\, =\, d\left ( 4,1 \right )\, =\, 8$$

$$Cost(i,s)=min\left\{Cos\left ( j,s-(j) \right )\, +\,d\left [ i,j \right ] \right\}$$

$$Cost(2,\left\{3 \right\},1)=d[2,3]\, +\, Cost\left ( 3,\Phi ,1 \right )\, =\, 9\, +\, 6\, =\, 15$$

$$Cost(2,\left\{4 \right\},1)=d[2,4]\, +\, Cost\left ( 4,\Phi ,1 \right )\, =\, 10\, +\, 8\, =\, 18$$

$$Cost(3,\left\{2 \right\},1)=d[3,2]\, +\, Cost\left ( 2,\Phi ,1 \right )\, =\, 13\, +\, 5\, =\, 18$$

$$Cost(3,\left\{4 \right\},1)=d[3,4]\, +\, Cost\left ( 4,\Phi ,1 \right )\, =\, 12\, +\, 8\, =\, 20$$

$$Cost(4,\left\{3 \right\},1)=d[4,3]\, +\, Cost\left ( 3,\Phi ,1 \right )\, =\, 9\, +\, 6\, =\, 15$$

$$Cost(4,\left\{2 \right\},1)=d[4,2]\, +\, Cost\left ( 2,\Phi ,1 \right )\, =\, 8\, +\, 5\, =\, 13$$

$$Cost(2,\left\{3,4 \right\},1)=min\left\{\begin{matrix} d\left [ 2,3 \right ]\,+ \,Cost\left ( 3,\left\{ 4\right\},1 \right )\, =\, 9\, +\, 20\, =\, 29 \\ d\left [ 2,4 \right ]\,+ \,Cost\left ( 4,\left\{ 3\right\},1 \right )\, =\, 10\, +\, 15\, =\, 25 \\ \end{matrix}\right.\, =\,25$$

$$Cost(3,\left\{2,4 \right\},1)=min\left\{\begin{matrix} d\left [ 3,2 \right ]\,+ \,Cost\left ( 2,\left\{ 4\right\},1 \right )\, =\, 13\, +\, 18\, =\, 31 \\ d\left [ 3,4 \right ]\,+ \,Cost\left ( 4,\left\{ 2\right\},1 \right )\, =\, 12\, +\, 13\, =\, 25 \\ \end{matrix}\right.\, =\,25$$

$$Cost(4,\left\{2,3 \right\},1)=min\left\{\begin{matrix} d\left [ 4,2 \right ]\,+ \,Cost\left ( 2,\left\{ 3\right\},1 \right )\, =\, 8\, +\, 15\, =\, 23 \\ d\left [ 4,3 \right ]\,+ \,Cost\left ( 3,\left\{ 2\right\},1 \right )\, =\, 9\, +\, 18\, =\, 27 \\ \end{matrix}\right.\, =\,23$$

$$Cost(1,\left\{2,3,4 \right\},1)=min\left\{\begin{matrix} d\left [ 1,2 \right ]\,+ \,Cost\left ( 2,\left\{ 3,4\right\},1 \right )\, =\, 10\, +\, 25\, =\, 35 \\ d\left [ 1,3 \right ]\,+ \,Cost\left ( 3,\left\{ 2,4\right\},1 \right )\, =\, 15\, +\, 25\, =\, 40 \\ d\left [ 1,4 \right ]\,+ \,Cost\left ( 4,\left\{ 2,3\right\},1 \right )\, =\, 20\, +\, 23\, =\, 43 \\ \end{matrix}\right.\, =\, 35$$

The minimum cost path is 35.

Start from cost {1, {2, 3, 4}, 1}, we get the minimum value for d [1, 2]. When s = 3, select the path from 1 to 2 (cost is 10) then go backwards. When s = 2, we get the minimum value for d [4, 2]. Select the path from 2 to 4 (cost is 10) then go backwards.

When s = 1, we get the minimum value for d [4, 2] but 2 and 4 is already selected. Therefore, we select d [4, 3] (two possible values are 15 for d [2, 3] and d [4, 3], but our last node of the path is 4). Select path 4 to 3 (cost is 9), then go to s = ϕ step. We get the minimum value for d [3, 1] (cost is 6).

Following are the implementations of the above approach in various programming languages −

Traveling Salesman Problem

The traveling salesman problem (TSP) asks the question, "Given a list of cities and the distances between each pair of cities, what is the shortest possible route that visits each city and returns to the origin city?".

This project

• The goal of this site is to be an educational resource to help visualize, learn, and develop different algorithms for the traveling salesman problem in a way that's easily accessible
• As you apply different algorithms, the current best path is saved and used as input to whatever you run next. (e.g. shortest path first -> branch and bound). The order in which you apply different algorithms to the problem is sometimes referred to the meta-heuristic strategy.

Heuristic algorithms

Heuristic algorithms attempt to find a good approximation of the optimal path within a more reasonable amount of time.

Construction - Build a path (e.g. shortest path)

• Shortest Path

Arbitrary Insertion

Furthest insertion.

• Nearest Insertion
• Convex Hull Insertion*
• Simulated Annealing*

Improvement - Attempt to take an existing constructed path and improve on it

• 2-Opt Inversion
• 2-Opt Reciprcal Exchange*

Exhaustive algorithms

Exhaustive algorithms will always find the best possible solution by evaluating every possible path. These algorithms are typically significantly more expensive then the heuristic algorithms discussed next. The exhaustive algorithms implemented so far include:

• Random Paths

Depth First Search (Brute Force)

• Branch and Bound (Cost)
• Branch and Bound (Cost, Intersections)*

Dependencies

These are the main tools used to build this site:

• web workers
• material-ui

Contributing

Pull requests are always welcome! Also, feel free to raise any ideas, suggestions, or bugs as an issue.

This is an exhaustive, brute-force algorithm. It is guaranteed to find the best possible path, however depending on the number of points in the traveling salesman problem it is likely impractical. For example,

• With 10 points there are 181,400 paths to evaluate.
• With 11 points, there are 1,814,000.
• With 12 points there are 19,960,000.
• With 20 points there are 60,820,000,000,000,000, give or take.
• With 25 points there are 310,200,000,000,000,000,000,000, give or take.

This is factorial growth, and it quickly makes the TSP impractical to brute force. That is why heuristics exist to give a good approximation of the best path, but it is very difficult to determine without a doubt what the best path is for a reasonably sized traveling salesman problem.

This is a recursive, depth-first-search algorithm, as follows:

• From the starting point
• For all other points not visited
• If there are no points left return the current cost/path
• Else, go to every remaining point and
• Mark that point as visited
• " recurse " through those paths (go back to 1. )

Implementation

Nearest neighbor.

This is a heuristic, greedy algorithm also known as nearest neighbor. It continually chooses the best looking option from the current state.

• sort the remaining available points based on cost (distance)
• Choose the closest point and go there
• Chosen point is no longer an "available point"
• Continue this way until there are no available points, and then return to the start.

Two-Opt inversion

This algorithm is also known as 2-opt, 2-opt mutation, and cross-aversion. The general goal is to find places where the path crosses over itself, and then "undo" that crossing. It repeats until there are no crossings. A characteristic of this algorithm is that afterwards the path is guaranteed to have no crossings.

• While a better path has not been found.
• For each pair of points:
• Reverse the path between the selected points.
• If the new path is cheaper (shorter), keep it and continue searching. Remember that we found a better path.
• If not, revert the path and continue searching.

This is an impractical, albeit exhaustive algorithm. It is here only for demonstration purposes, but will not find a reasonable path for traveling salesman problems above 7 or 8 points.

I consider it exhaustive because if it runs for infinity, eventually it will encounter every possible path.

• From the starting path
• Randomly shuffle the path
• If it's better, keep it
• If not, ditch it and keep going

This is a heuristic construction algorithm. It select a random point, and then figures out where the best place to put it will be.

• First, go to the closest point
• Choose a random point to go to
• Find the cheapest place to add it in the path
• Continue from #3 until there are no available points, and then return to the start.

Two-Opt Reciprocal Exchange

This algorithm is similar to the 2-opt mutation or inversion algorithm, although generally will find a less optimal path. However, the computational cost of calculating new solutions is less intensive.

The big difference with 2-opt mutation is not reversing the path between the 2 points. This algorithm is not always going to find a path that doesn't cross itself.

It could be worthwhile to try this algorithm prior to 2-opt inversion because of the cheaper cost of calculation, but probably not.

• Swap the points in the path. That is, go to point B before point A, continue along the same path, and go to point A where point B was.

Branch and Bound on Cost

This is a recursive algorithm, similar to depth first search, that is guaranteed to find the optimal solution.

The candidate solution space is generated by systematically traversing possible paths, and discarding large subsets of fruitless candidates by comparing the current solution to an upper and lower bound. In this case, the upper bound is the best path found so far.

While evaluating paths, if at any point the current solution is already more expensive (longer) than the best complete path discovered, there is no point continuing.

For example, imagine:

• A -> B -> C -> D -> E -> A was already found with a cost of 100.
• We are evaluating A -> C -> E, which has a cost of 110. There is no point evaluating the remaining solutions.

Instead of continuing to evaluate all of the child solutions from here, we can go down a different path, eliminating candidates not worth evaluating:

• A -> C -> E -> D -> B -> A
• A -> C -> E -> B -> D -> A

Implementation is very similar to depth first search, with the exception that we cut paths that are already longer than the current best.

This is a heuristic construction algorithm. It selects the closest point to the path, and then figures out where the best place to put it will be.

• Choose the point that is nearest to the current path

Branch and Bound (Cost, Intersections)

This is the same as branch and bound on cost, with an additional heuristic added to further minimize the search space.

While traversing paths, if at any point the path intersects (crosses over) itself, than backtrack and try the next way. It's been proven that an optimal path will never contain crossings.

Implementation is almost identical to branch and bound on cost only, with the added heuristic below:

This is a heuristic construction algorithm. It selects the furthest point from the path, and then figures out where the best place to put it will be.

• Choose the point that is furthest from any of the points on the path

Convex Hull

This is a heuristic construction algorithm. It starts by building the convex hull , and adding interior points from there. This implmentation uses another heuristic for insertion based on the ratio of the cost of adding the new point to the overall length of the segment, however any insertion algorithm could be applied after building the hull.

There are a number of algorithms to determine the convex hull. This implementation uses the gift wrapping algorithm .

In essence, the steps are:

• Determine the leftmost point
• Continually add the most counterclockwise point until the convex hull is formed
• For each remaining point p, find the segment i => j in the hull that minimizes cost(i -> p) + cost(p -> j) - cost(i -> j)
• Of those, choose p that minimizes cost(i -> p -> j) / cost(i -> j)
• Add p to the path between i and j
• Repeat from #3 until there are no remaining points

Simulated Annealing

Simulated annealing (SA) is a probabilistic technique for approximating the global optimum of a given function. Specifically, it is a metaheuristic to approximate global optimization in a large search space for an optimization problem.

For problems where finding an approximate global optimum is more important than finding a precise local optimum in a fixed amount of time, simulated annealing may be preferable to exact algorithms

Visualize algorithms for the traveling salesman problem. Use the controls below to plot points, choose an algorithm, and control execution. (Hint: try a construction alogorithm followed by an improvement algorithm)

• Graph Theory

Travelling Salesman in a Grid

The travelling salesman has a map containing m*n squares. He starts from the top left corner and visits every cell exactly once and returns to his initial position (top left). The time taken for the salesman to move from a square to its neighbor might not be the same. Two squares are considered adjacent if they share a common edge and the time taken to reach square b from square a and vice-versa are the same. Can you figure out the shortest time in which the salesman can visit every cell and get back to his initial position?

Input Format

The first line of the input is 2 integers m and n separated by a single space. m and n are the number of rows and columns of the map. Then m lines follow, each of which contains (n – 1) space separated integers. The j th integer of the i th line is the travel time from position (i,j) to (i,j+1) (index starts from 1.) Then (m-1) lines follow, each of which contains n space integers. The j th integer of the i th line is the travel time from position (i,j) to (i + 1, j).

Constraints

1 ≤ m, n ≤ 10 Times are non-negative integers no larger than 10000.

Output Format

Just an integer contains the minimal time to complete his task. Print 0 if its not possible to visit each cell exactly once.

Sample Input

Sample Output

Explanation

As its a 2*2 square, all cells are visited. 5 + 7 + 8 + 6 = 26

Cookie support is required to access HackerRank

Seems like cookies are disabled on this browser, please enable them to open this website

• Data Structures
• Linked List
• Binary Tree
• Binary Search Tree
• Segment Tree
• Disjoint Set Union
• Fenwick Tree
• Red-Black Tree
• Advanced Data Structures
• Edge Relaxation Property for Dijkstra’s Algorithm and Bellman Ford's Algorithm
• Branch and Bound Algorithm
• Job Assignment Problem using Branch And Bound
• Check if incoming edges in a vertex of directed graph is equal to vertex itself or not
• Channel Assignment Problem
• A Peterson Graph Problem
• Determining topology formed in a Graph
• Maximum number of soldier in a team
• Graph Data Structure And Algorithms
• Successor Graph
• Construct a graph from given degrees of all vertices
• Stable Marriage Problem
• Push Relabel Algorithm | Set 2 (Implementation)
• Shortest path with one curved edge in an undirected Graph
• Check if there exists a connected graph that satisfies the given conditions
• Shortest path in a graph from a source S to destination D with exactly K edges for multiple Queries
• Two Clique Problem (Check if Graph can be divided in two Cliques)
• Traveling Salesman Problem using Branch And Bound
• Largest subset of Graph vertices with edges of 2 or more colors

Travelling Salesman Problem (TSP) using Reduced Matrix Method

Given a set of cities and the distance between every pair of cities, the problem is to find the shortest possible route that visits every city exactly once and returns to the starting point. 

Input:   Example of connections of cities Output: 80 Explanation: An optimal path is 1 – 2 – 4 – 3 – 1.

Dynamic Programming Approach: This approach is already discussed in Set-1 of this article.

Branch and Bound Approach: The branch and bound approach is already discussed in this article .

Reduced Matrix: This approach is similar to the Branch and Bound approach. The difference here is that the cost of the path and the bound is decided based on the method of matrix reduction. The following are the assumptions for a reduced matrix:

• A row or column of the cost adjacency matrix is said to be reduced if and only if it contains at least one zero element and all remaining entries in that row or column ≥ 0.
• If all rows and columns are reduced then only the matrix is reduced matrix. 
• Tour length (new) = Tour length (old) – Total value reduced.
• We first rewrite the original cost adjacency matrix by replacing all diagonal elements from 0 to Infinity 

The basic idea behind solving the problem is:

The cost to reduce the matrix initially is the minimum possible cost for the travelling salesman problem. Now in each step, we need to decide the minimum possible cost if that path is taken i.e., a path from vertex u to v is followed.  We can do that by replacing uth row and vth column cost by infinity and then further reducing the matrix and adding the extra cost for reduction and cost of edge (u, v) with the already calculated minimum path cost. Once at least one path cost is found, that is then used as upper bound of cost to apply the branch and bound method on the other paths and the upper bound is updated accordingly when a path with lower cost is found.

Following are the steps to implement the above procedure:

• Step1: Create a class (Node) that can store the reduced matrix, cost, current city number, level (number of cities visited so far), and path visited till now. 
• Step2: Create a priority queue to store the live nodes with the minimum cost at the top. 
• Row reduction – Find the min value for each row and store it. After finding the min element from each row, subtract it from all the elements in that specific row. 
• Column reduction – Find the min value for each column and store it. After finding the min element from each column, subtract it from all the elements in that specific column. Now the matrix is reduced.
• Now add all the minimum elements in the row and column found earlier to get the cost. 
• Step4: Push the element with all information required by Node into the Priority Queue. 
• Pop the element with the min value from the priority queue.
• For each pop operation check whether the level of the current node is equal to the number of nodes/cities or not. 
• If yes then print the path and return the minimum cost.
• The cost of a reduced Matrix can be calculated by converting all the values of its rows and column to infinity and also making the index Matrix[Col][row] = infinity. 
• Then again push the current node into the priority queue. 
• Step6: Repeat Step5 till we don’t reach the level = Number of nodes – 1.

Follow the illustration below for a better understanding.

Illustration:

Consider the connections as shown in the graph: Example of connections Initially the cost matrix looks like: row/col no 1 2 3 4 1 – 10 15 20 2 10 – 35 25 3 15 35 – 30 4 20 25 30 – After row and column reduction the matrix will be: row/col no 1 2 3 4 1 – 0 5 10 2 0 – 25 15 3 0 20 – 15 4 0 5 10 – and row minimums are 10, 10, 15 and 20. row/col no 1 2 3 4 1 – 0 0 0 2 0 – 20 5 3 0 20 – 5 4 0 5 5 – and the column minimums are 0, 0, 5 and 10. So the cost reduction of the matrix is (10 + 10 + 15 + 20 + 5 + 10) = 70 Now let us consider movement from 1 to 2: Initially after substituting the 1st row and 2nd column to infinity, the matrix will be: row/col no 1 2 3 4 1 – – – – 2 – – 20 5 3 0 – – 5 4 0 – 5 – After the matrix is reduced the row minimums will be 5, 0, 0  row/col no 1 2 3 4 1 – – – – 2 – – 15 0 3 0 – – 5 4 0 – 5 – and the column minimum will be  0, 5, 0 row/col no 1 2 3 4 1 – – – – 2 – – 10 0 3 0 – – 5 4 0 – 0 – So the cost will be 70 + cost (1, 2) + 5 + 5 = 70 + 0 + 5 + 5 = 80. Continue this process till the traversal is complete and find the minimum cost. Given below the structure of the recursion tree along with the bounds: The recursion diagram with bounds

Below is the implementation of the above approach.

Time Complexity: O(2 N * N 2 ) where N = number of node/ cities. Space Complexity: O(N 2 )

Please Login to comment...

Similar reads.

• Branch and Bound
• How to Use ChatGPT with Bing for Free?
• 7 Best Movavi Video Editor Alternatives in 2024
• How to Edit Comment on Instagram
• 10 Best AI Grammar Checkers and Rewording Tools
• 30 OOPs Interview Questions and Answers (2024)

Improve your Coding Skills with Practice

What kind of Experience do you want to share?