travelling salesman problem bitmask

• Submissions

kartik8800's blog

Introduction to DP with Bitmasking

Hello Codeforces!

This series of videos are focused on explaining dynamic programming by illustrating the application of DP with bitmasking through the use of selected problems from platforms like Codeforces, Codechef, SPOJ, CSES and Atcoder.

After going through this series, you should find yourself confident in solving problems which require the use of dp and bitmasks and also implementing them in a reasonable amount of time.

I will also live code and submit the solutions to the problem on the coding platform from where the problem comes.

Some Basic elements of Dynamic Programming

Some general ideas and my thoughts about DP to help you get started:

Part 1: https://youtu.be/24hk2qW_BCU 1. What is Divide and Conquer? 2. What is Dynamic Programming? 3. Types of DP problems.

Part 2: https://youtu.be/yfgKw6BUZUk 1. What is a DP-state? 2. Characterizing a DP-state. 3. What is a recurrence? 4. Top Down v/s Bottom Up.

Part 3: https://youtu.be/X-3HklSPx6k 1. Directed Acyclic Graph(DAG) Representation of DP solution 2. Visualizing Top-Down and Bottom-Up. 3. Evaluation order for bottom-up codes. 4. Analyzing the space and time complexity for a DP solution(derivation).

You may also want to checkout these video tutorials: - Beginner Friendly Series on Dynamic Programming - Dynamic Programming on Trees

About the series

Short video where I talk about the playlist: https://youtu.be/6sEFap7hIl4

What is Bitmasking

I talk about what is bitmasking before we actually start solving problems that use dp with bitmasking. https://youtu.be/7FmL-WpTTJ4

Illustration: Solving the Job Assignment Problem

Using a simple problem, I will illustrate how to solve and implement problems which use dp+bitmask concepts. Problem link: statement Solution: https://youtu.be/685x-rzOIlY

Illustration: Travelling Salesman Problem

Another great problem to illustrate bitmask dp. I will discuss the following: 1. What is the TSP? 2. Brute force solution. 3. Intuition towards an efficient solution. 4. Define a DP state, write a recurrence. 5. How do I implement this? ANS: bitmasking! 6. Analyzing time and space complexities.

Link: https://youtu.be/QukpHtZMAtM

Codeforces Problem: Div2E

I'll discuss a problem named Fish that comes from a Codeforces Divison 2 round. Problem link: https://codeforces.com/contest/16/problem/E Solution: https://youtu.be/d7kvyp6dfz8

Codechef long Challenge: Medium

The problem comes from Codechef long challenge and is rated MEDIUM by codechef. Problem link: https://www.codechef.com/problems/TSHIRTS Solution: https://youtu.be/Smem2tVQQXU

CSES: Counting Tilings

The problem comes from CSES problemset and was introduced to the problemset in 2021. Problem link: https://cses.fi/problemset/task/2181 Solution: https://youtu.be/lPLhmuWMRag

Practice Problems: 1. https://atcoder.jp/contests/dp/tasks/dp_o 2. https://atcoder.jp/contests/dp/tasks/dp_u 3. https://www.codechef.com/JAN13/problems/LEALCO 4. https://www.spoj.com/problems/HIST2/ 5. https://codeforces.com/problemset/problem/895/C

If people find this helpful then I will try and add more problems to this list :)

Search anything:

Travelling Salesman Problem (Bitmasking and Dynamic Programming)

Algorithms graph algorithms dynamic programming (dp) bitwise algorithm.

Open-Source Internship opportunity by OpenGenus for programmers. Apply now.

In this article we will start our discussion by understanding the problem statement of The Travelling Salesman Problem perfectly and then go through the basic understanding of bit masking and dynamic programming .

What is the problem statement ?

Travelling Salesman Problem is based on a real life scenario, where a salesman from a company has to start from his own city and visit all the assigned cities exactly once and return to his home till the end of the day. The exact problem statement goes like this, "Given a set of cities and distance between every pair of cities, the problem is to find the shortest possible route that visits every city exactly once and returns to the starting point."

There are two important things to be cleared about in this problem statement,

• Visit every city exactly once
• Cover the shortest path

What is the need of Dynamic Programming ?

If we look into the brute force approach for solving this problem, we can see that due to recursion call, a lot of cases are repeating themselves and that's the reason of a bigger runtime. The code for the brute force approach can be found below,

As it can be deduced easily from the above code that, the time complexity is O(n!) and the space complexity is O(n^2) . By using dynamic programming we can save the repeated cases when they are calculated for the first time, and next time when we need the result we can directly use them from our storage(in terms of data structures).

What is the need of Bit Masking ?

As you might know, computer hardwares natively support binary digits(bits) i.e. 0 for false and 1 for true. In other language we can compile that 0 means not occupied and 1 means occupied.

We can break the problem into three different parts,

• Constructing and maintaining another 2D array which stores the shortest path sum values for each (i,j), whcih means in this matrix, value at (i,j) denotes the weight of the shortest path at any instance of the program run.
• Maintaining one visited variable, which in terms denote the total possible permutations of the cities.
• Finally we will be checking if a city is visited before. We will be using bitwise & and bitwise left shift << operator to get into the solution.

Steps To Solve the Problem

There are few classical and easy steps that we must follow to solve the TSP problem,

• Finding Adjacent matrix of the graph, which will act as an input.
• performing the shortest_path algorithm with the help of bitmasking and dynamic programming, by coding out a function.
• Understanding the bitwise operators.

Step-1 - Finding Adjacent Matrix Of the Graph

You will need a two dimensional array for getting the Adjacent Matrix of the given graph. Here are the steps;

• Get the total number of nodes and total number of edges in two variables namely num_nodes and num_edges.
• Create two multidimensional arrays, edges_list having the dimension equal to num_nodes * num_nodes and dp_array having the dimension equal to total number of permutations m, which is interms equal to (1<<num_nodes). Set all the dp_array entries to -1, which will act as a check point integer in the core algorithm.
• Run a loop num_nodes time and take two inputs namely first_node and second_node * everytime as two nodes having an edge between them and place the edges_list[first_node][second_node] position equal to 1.
• Finally after the loop executes we have an adjacent matrix available i.e edges_list.

Step - 2 - Performing The Shortest Path Algorithm using Dynamic Programming and Bitmasking

The most important step in designing the core algorithm is this one, let's have a look at the pseudocode of the algorithm below. We will be considering a small example and try to understand each of the following steps.

What is a mask ?

Let's consider the following graph as an example, where we have four cities named A,B,C,D and there are six weighted edges between them as shown in the figure.

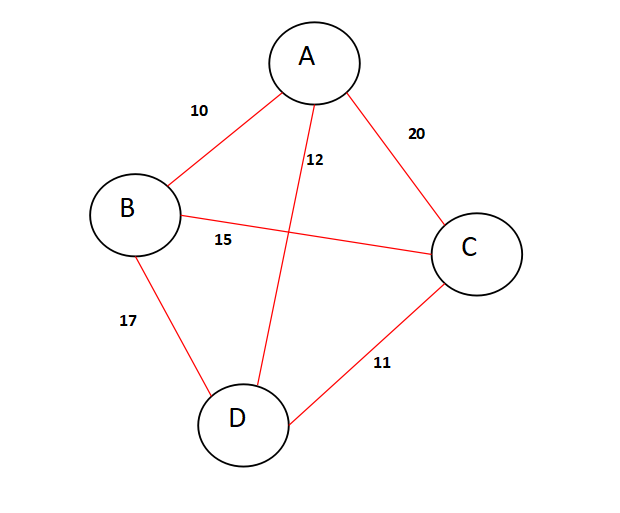
So for the salesman to cover all the cities and return to the main city, he has to visit each city once. Lets consider 4 bits for A,B,C,D where 0 in a bit represents the city is not visited and 1 represented the city is visited. So for the visited variable in the algorithm, we are considering all the citities already visited and that gives us a bit representation of 1 1 1 1 . Have a look at the following diagram.

As we can see this bit representation will give use an integer representation equal to (2^4 - 1) , which can be otherwise written as (1<<4) - 1 . The aim of using bitwise operators like leftshift instead of using pow() etc is that, bits work on a hardware level which are faster. This deduce our first step of assigning the visited variable a value which is equal to (1<<num_nodes)-1 .

The next step is to interpret the importance of mask.

mask is nothing but a checker if all the nodes/cities are visited. Suppose the salesman starts from node A. It means the value of mask will be 0 0 0 1 , which is 1 in integer format. As soon as the salesman visits B it become 0 0 1 1 . If the salesman visits C in the second and not B then it becomes 0 1 0 1 . And when he visits all the cities once, we get mask same as that of visited, i.e. 1 1 1 1 .

This serves as the base case of our algorithm. When the mask is equal to visited we retrun something. But what to return ? We will discuss next.

What is the work of position here ?

The position stores the position of the salesman at any point of time. As we are starting from city A or we may call it as source city and denote it as 0 in our adjacency matrix, the initial position is 0. The sales man moves from city 0 to city 4 and returns back to 0.

The position value varies with city with every recursive call.

When our basecase is satisfied we will return the adjacency matrix value at the (position,source_city) coordinate, which signifies the direct path value between the position and the source.

The DP array and it's usages

The work of the dp_array here is to store the minimum possible path value of two nodes i and j at the array position (i,j). The -1 value works as a checker. If the value of certain (i,j) is -1 means the weight of the shortest path has not been calculated between i and j.

Here we perform another check that if the dp_array value for (mask,position) is not equal to -1 then return the original value at that position.

The sole aim of this step is to avoid repeatation that has occured during normal recursive solution.

The normal calculataion

And here comes the final normal calculation or we can say the core calculataion for this algorithm. This calculation will only take place if the base case and the check case gets false.

• We will be maintaining a variable named ans for getting the minimum path and assign it to INT_MAX at the beginning.
• We will be calling a loop from city= 0 to the city = n
• Perform a recursive call and save the output in a integer varaible named newAns .
• Later we will be getting the minimum of ans and newAns and assigning the same to the dp_array for memorization purpose.
• Finally return the dp_array value at (mask,position).

The Total Code

Time & space complexity.

We have recursive calls here as well as loops. In fact we have recursive call inside loops.

It can be derived that the space complexity will be O(V^2) where V is the number of nodes/cities here.

For the time complexity we need to look into a little bit deeper. As we can see we have a recurrance relation here in terms of recursion, which is a subproblem and each subproblem takes linear time to get the output,i.e. O(V * 2^V) .This recursive call happens inside a loop havinbg runtime of O(V) . Hence we have a total runtime of O(V^2 * 2^V) , which is exponential.

• [email protected]

What’s New ?

The Top 10 favtutor Features You Might Have Overlooked

• Don’t have an account Yet? Sign Up

Remember me Forgot your password?

• Already have an Account? Sign In

Lost your password? Please enter your email address. You will receive a link to create a new password.

Back to log-in

By Signing up for Favtutor, you agree to our Terms of Service & Privacy Policy.

Travelling Salesman Problem using Dynamic Programming

• Jun 17, 2023
• 7 Minutes Read
• Why Trust Us We uphold a strict editorial policy that emphasizes factual accuracy, relevance, and impartiality. Our content is crafted by top technical writers with deep knowledge in the fields of computer science and data science, ensuring each piece is meticulously reviewed by a team of seasoned editors to guarantee compliance with the highest standards in educational content creation and publishing.
• By Harshita Rajput

Imagine you have to go to a party in another city and return back home as soon as possible. Which algorithm will you apply to reach your home so that you cover the shortest distance? Let us understand Travelling Salesman Problem in this guide.

What is Traveling Salesman Problem?

The Traveling Salesman Problem classic optimization problem in Computer Science. There is a salesman who wants to travel over a number of cities and he has to return back to the original city he started from and he has the choice to start from any of the cities he wants to. During his journey, we need to minimize the total distance traveled by him. 

Here is the main problem statement:

" We will be given a graph that will be represented in the form of an adjacency matrix, say distance, that denotes the distance between 2 cities, say, i and j. The distance[i][j] denotes the distance between 2 cities if the value of dist[i][j] == 0; this implies the given cities are not connected i.e. no direct edge exists between them. We can start from any node and we need to return to the original city through the shortest distance covering all the cities. "

So, basically, we need to complete a cycle in this question, and such a cycle is known as the Hamiltonian cycle. A Hamiltonian cycle is a set of edges such that every node is visited only once and we come back to the original position. So in short, in this problem, we need to return a minimum weight Hamiltonian cycle. We just have to minimize the total cost of the cycle.

Let's first try to get a Hamiltonian cycle with minimum weight from the graph below. Given the following graph and the distance between cities he has traveled, let's find out the shortest path in which he can travel all the cities.

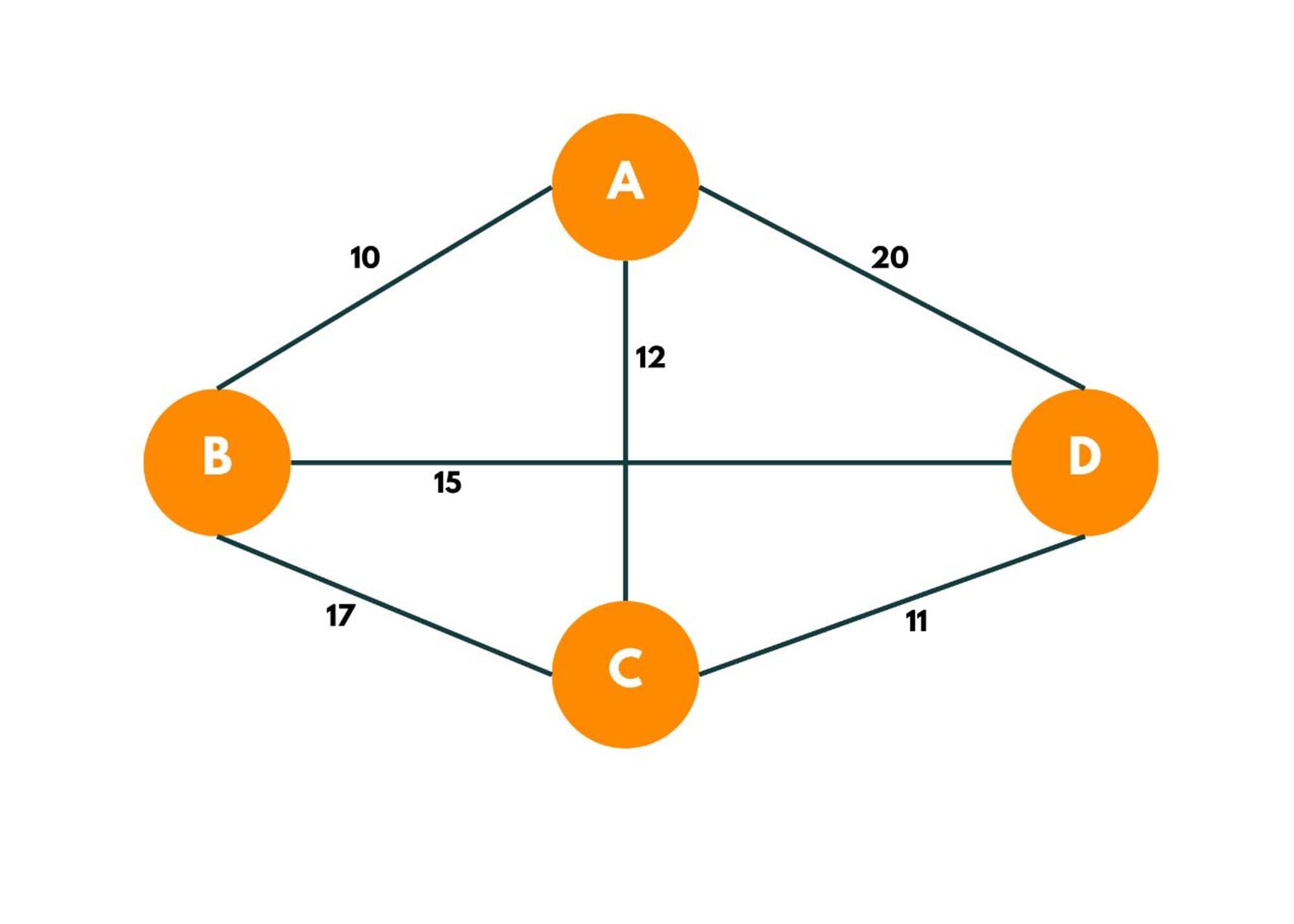
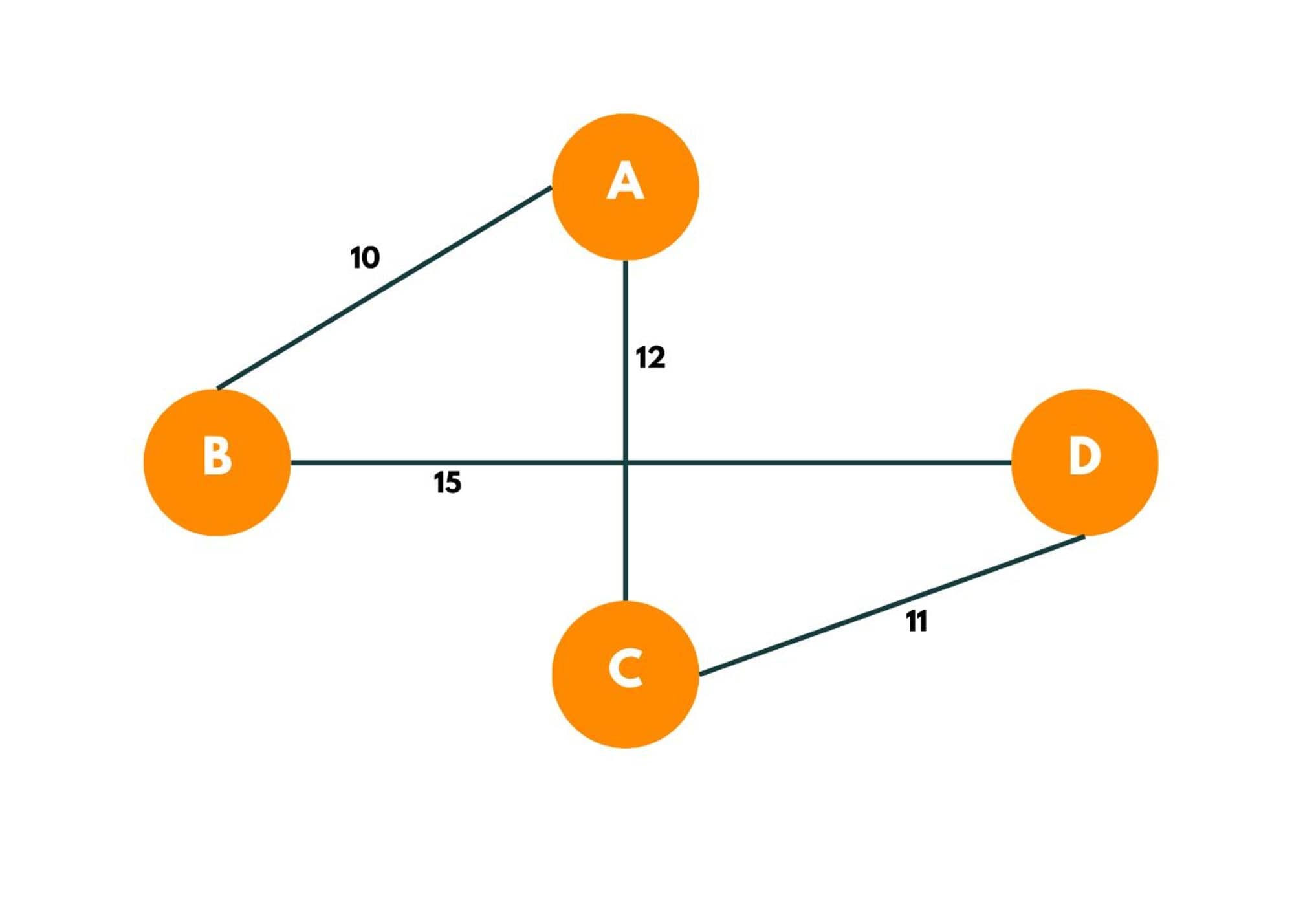
The Hamiltonian cycle with min weight can be:

How does the Algorithm Work?

Let's take an example of a graph say:

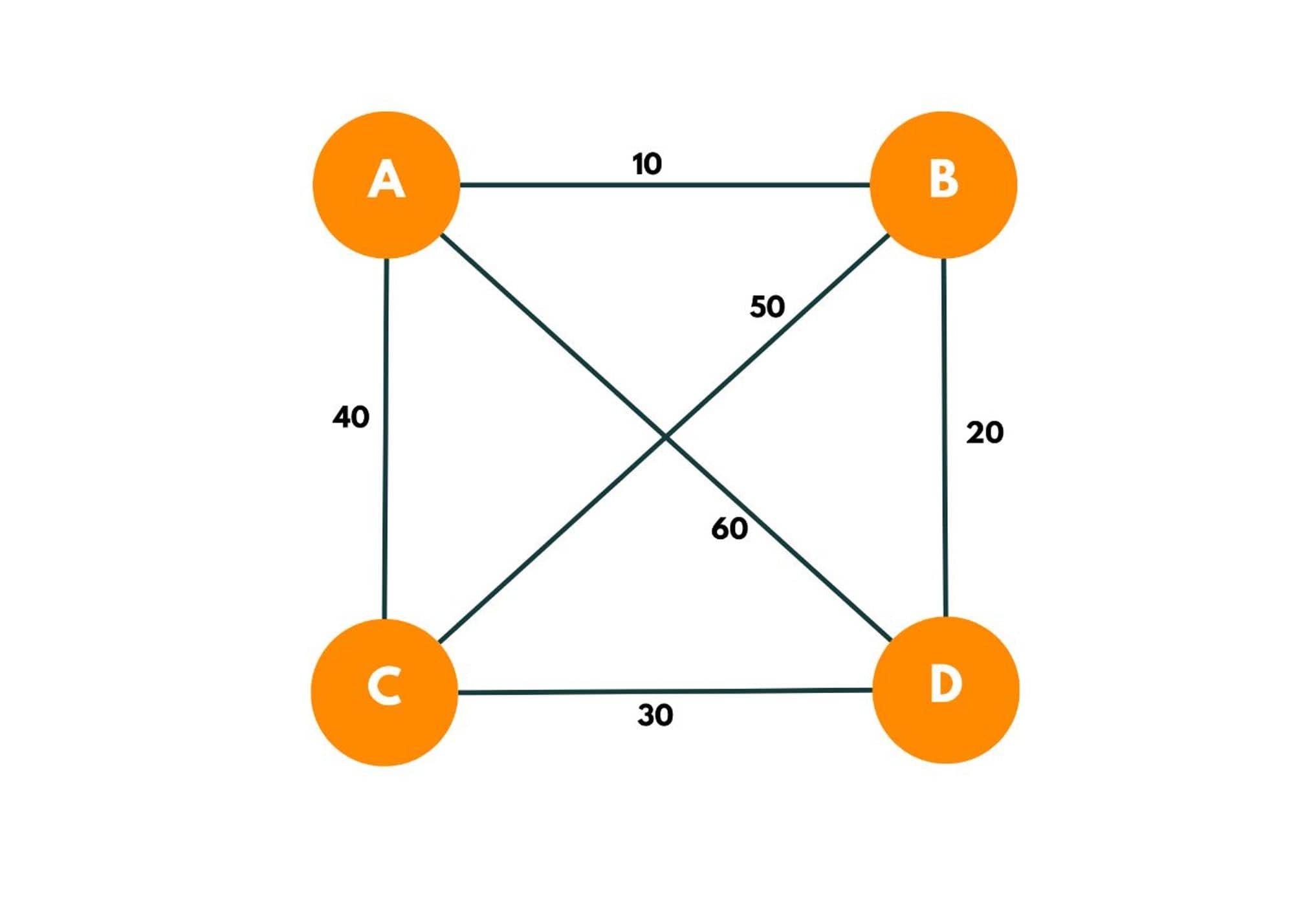
• As we have an option to start from any position, we start from A.
• Making a recursion tree and using bit masking. 

As 4 cities are there, the bit mask here would be = 0000 (at the beginning) respectively denoting D, C, B, and A  cities. The bit shows 0 for a particular city if it has not been visited and 1 if already been visited. So if bit mask = 1111 that means all bits are set, which implies all cities have been visited and we can denote this by 1<

We try to find the possible options that exist. This can be done by iterating over the adjacency matrix of A or the other way of doing so can be iterating over other cities and checking if they can be a possible option to travel from A. As we begin, we visit city A, and the bit mask value is now changed to 0001.

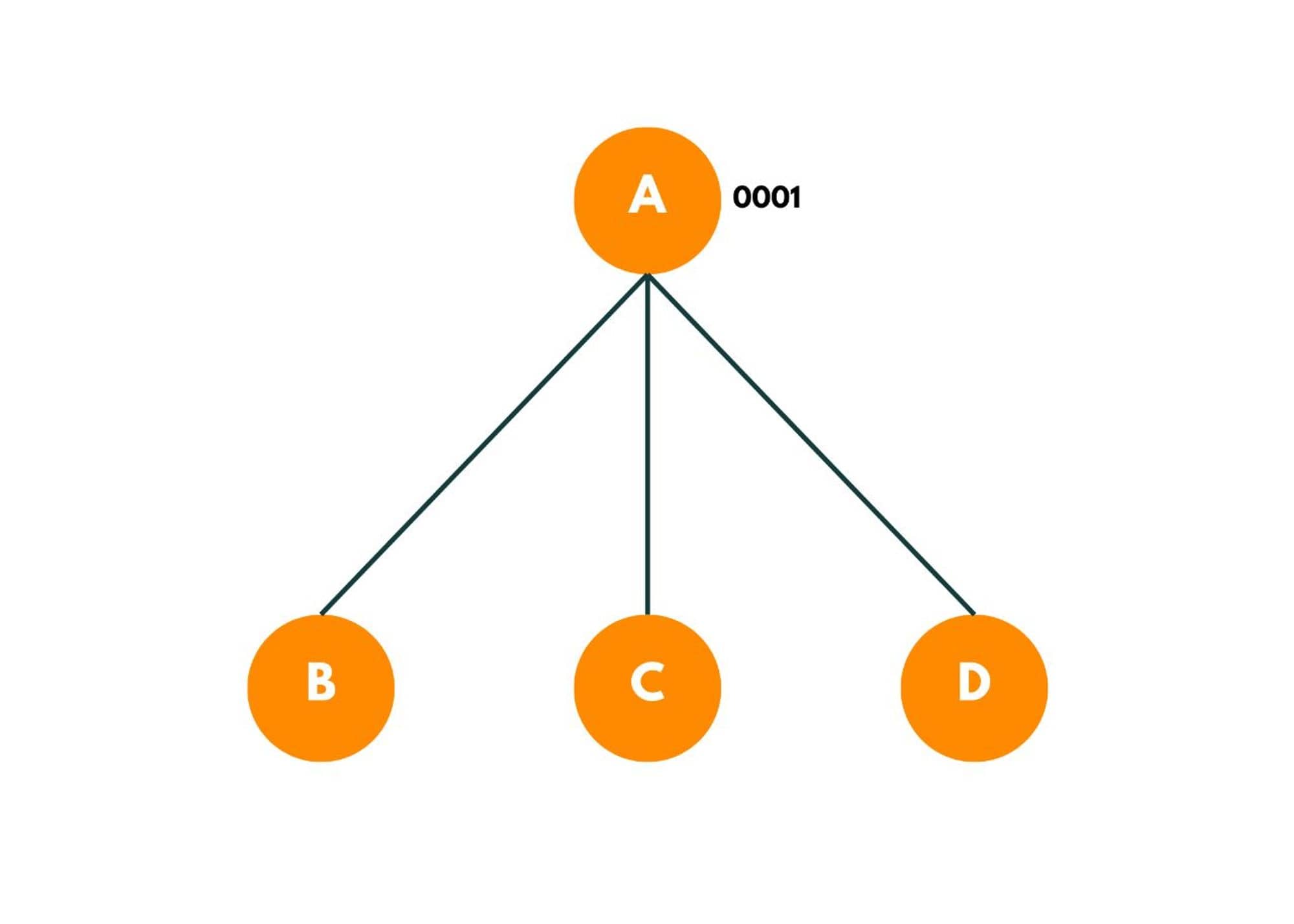
Each of these recursive branches denotes one path.

Now, as we move forward from A to B, we add the distance in a variable, say, ans. And we mark city B as visited.

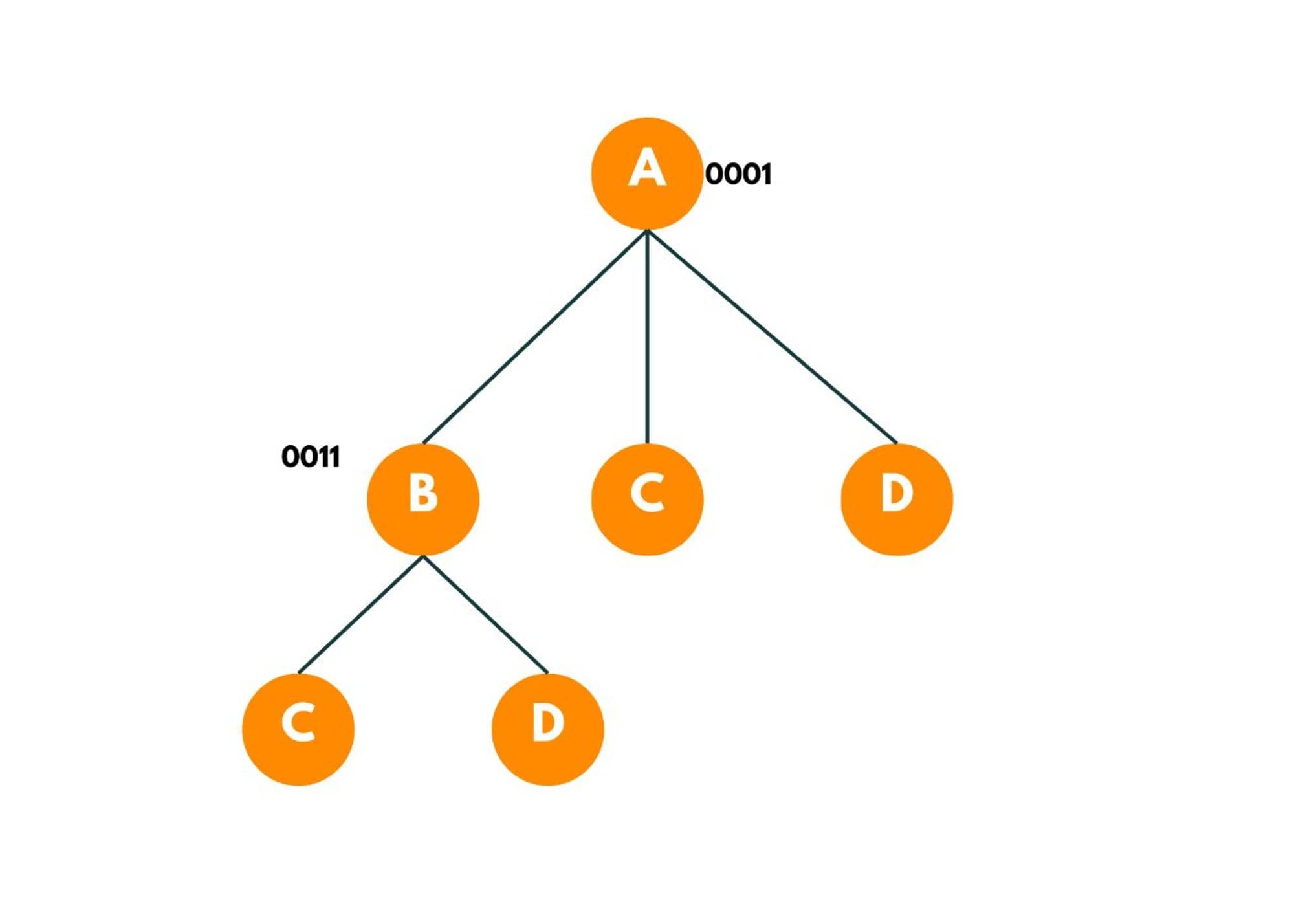
We add the distance to the answer. Now we only visit the cities from B that aren't visited yet so we have 2 options available C and D.

We then move to C and then to D while marking them visited and adding the cost to the and. Now here, we have explored each unvisited city. So now we backtrack, while marking each city as unvisited and go to the original city if a direct edge between them exists. As there is a direct edge from D to A and C to A, the nodes return the cost required to go back to the original source.

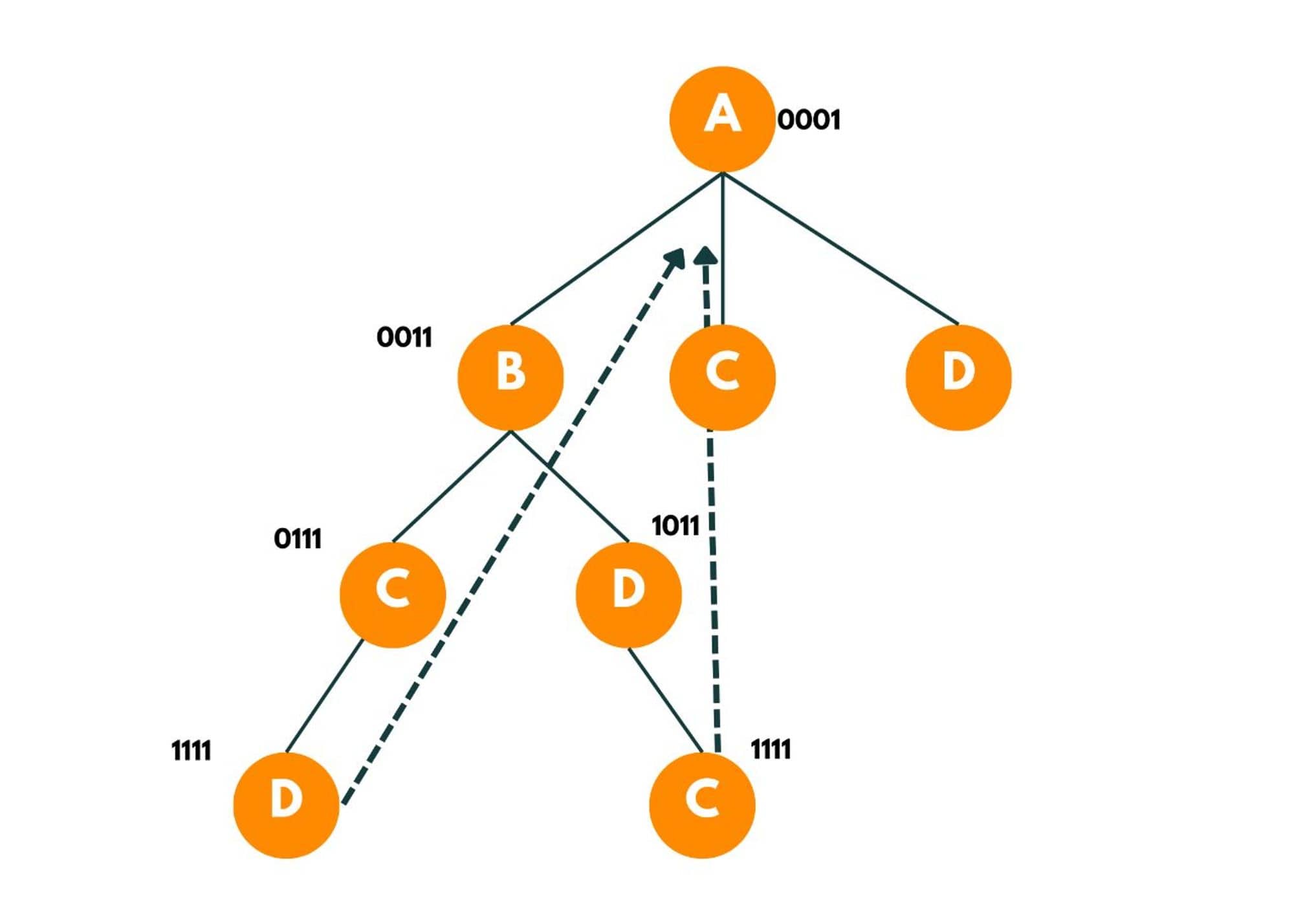
This way we explore each available option from the starting node. We also maintain a minimum cost variable that maintains the minimum cost spent to visit each city and return to the original city.

The recursion tree would look like this:

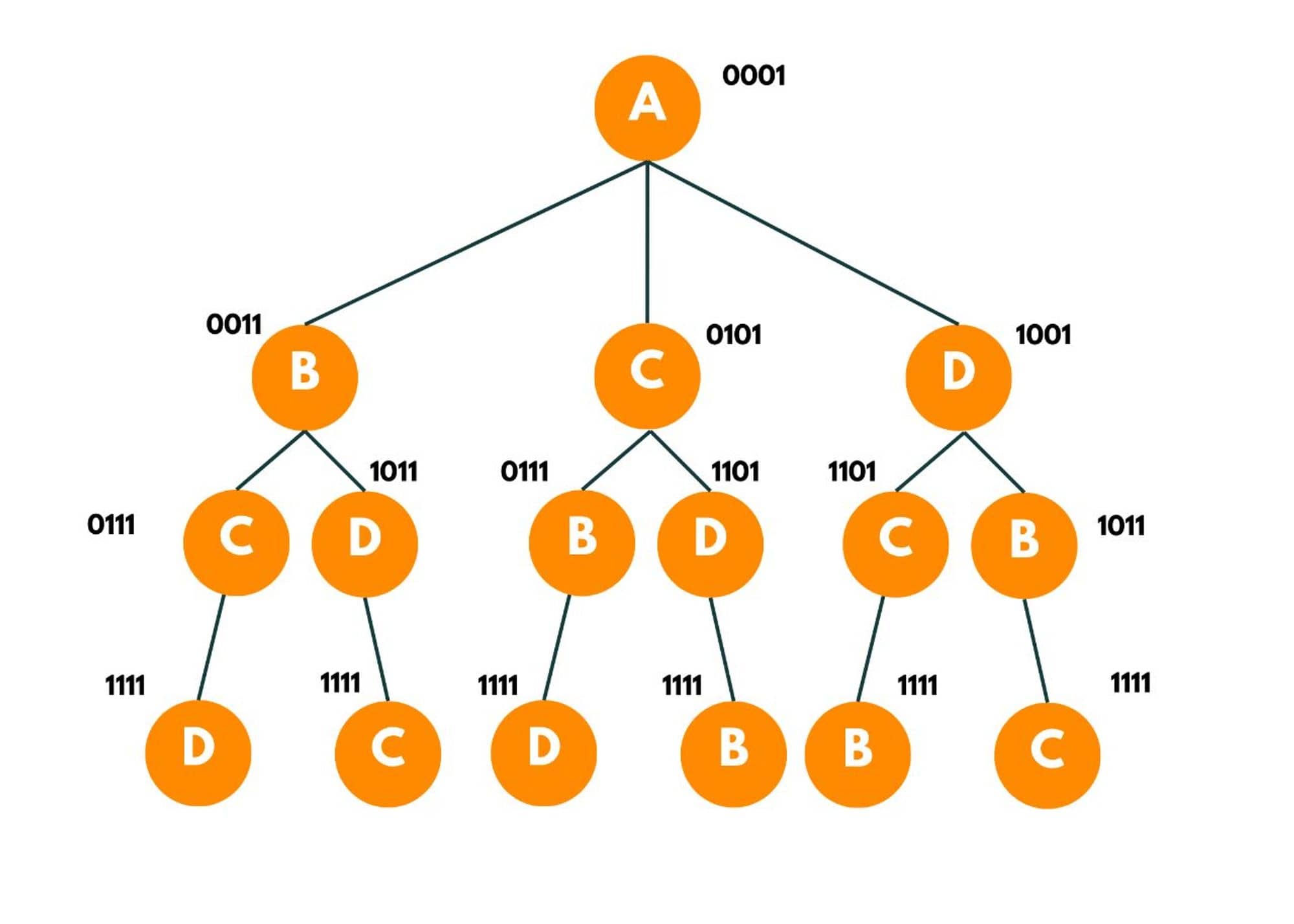
Traveling Salesman Algorithm

Here is the algorithm for Travelling Salesman Problem:

• Define the mask as (1<<n)-1.
• Create a function, say, tsp() having mask and city as arguments. As the mask denotes a set of cities visited so far, we iterate over the mask and get to know which city isn't visited.
• The base case is when we visit all the cities i.e. mask has all of its bits set, we return the distance between the current city and the original city.
• If the city is not visited, we make recursive calls by adding the distance of the original city and the city not visited and try to get the distance remaining from recursive calls
• In the recursive call, we pass a mask with the current city visited and the current city.

Travelling Salesman Problem in Java

Here is the complete Java Program to implement Travelling Salesman Problem:

Time & Space Complexity 

Here we have fixed the source node as we get the same answer whether we start from A or B or any other node because of that cyclic permutation in this case.

The time complexity of the Travelling Salesman Problem comes out to be O(n-1!). The space complexity of this code comes out to be O(n).

Now we can notice that this bitmask can only have 2^n values ranging from 0000 to 1111. The city can take n values. So the total number of distinct states comes out to be (2^n )* n. Also in this approach, some sub-problems were getting overlapped.

To optimize this approach, we use DP. We will create a 2D DP table of the values and we memorize all the results for the given value of mask and city.

Optimized Approach using Dynamic Programming

Here is the simple way to implement the Optimized Approach using Dynamic Programming. Initially we make a 2D array of [2^n][n] and initially put -1 at each position as initially, all states have values = -1.

To avoid overlapping subproblems i.e. avoiding a state which has already been computed, we check dp[bitMask][city]. If this comes out to be -1, implies the city hasn't been visited, else the city has already been visited and we return dp[bitMask][city] = ans.

Here is the Java Code for Travelling Salesman Problem using Dynamic Programming:

The time complexity comes out to be O(n ^2 * (2*n)). As we are using an extra space of (2^n) *n. The space complexity comes out to be O((2^n) *n).

Conclusion 

Travelling Salesman is a classic problem demanding in-depth knowledge of graphs and DP. It is an NP-hard problem. The optimization used in this problem can be implemented in other questions of this type too. This problem is necessary from the interview point of view, so I hope you all understood it well!

FavTutor - 24x7 Live Coding Help from Expert Tutors!

About The Author

Harshita Rajput

More by favtutor blogs, monte carlo simulations in r (with examples), aarthi juryala.

The unlist() Function in R (with Examples)

Paired Sample T-Test using R (with Examples)

# Travelling Salesman

# brute force algorithm.

A path through every vertex exactly once is the same as ordering the vertex in some way. Thus, to calculate the minimum cost of travelling through every vertex exactly once, we can brute force every single one of the N! permutations of the numbers from 1 to N .

Time Complexity

There are N! permutations to go through and the cost of each path is calculated in O(N) , thus this algorithm takes O(N * N!) time to output the exact answer.

# Dynamic Programming Algorithm

Notice that if we consider the path (in order):

and the path

The cost of going from vertex 1 to vertex 2 to vertex 3 remains the same, so why must it be recalculated? This result can be saved for later use.

Let dp[bitmask][vertex] represent the minimum cost of travelling through all the vertices whose corresponding bit in bitmask is set to 1 ending at vertex . For example:

Since 12 represents 1100 in binary, dp[12][2] represents going through vertices 2 and 3 in the graph with the path ending at vertex 2.

Thus we can have the following algorithm (C++ implementation):

This line may be a little confusing, so lets go through it slowly:

Here, bitmask | (1 << i) sets the ith bit of bitmask to 1, which represents that the ith vertex has been visited. The i after the comma represents the new pos in that function call, which represents the new "last" vertex. cost[pos][i] is to add the cost of travelling from vertex pos to vertex i .

Thus, this line is to update the value of cost to the minimum possible value of travelling to every other vertex that has not been visited yet.

The function TSP(bitmask,pos) has 2^N values for bitmask and N values for pos . Each function takes O(N) time to run (the for loop). Thus this implementation takes O(N^2 * 2^N) time to output the exact answer.

The Travelling Salesman Problem is the problem of finding the minimum cost of travelling through N vertices exactly once per vertex. There is a cost cost[i][j] to travel from vertex i to vertex j .

There are 2 types of algorithms to solve this problem: Exact Algorithms and Approximation Algorithms

Exact Algorithms

• Brute Force Algorithm
• Dynamic Programming Algorithm

Approximation Algorithms

To be added

← Hash Functions Shortest Common Supersequence Problem →

• Data Structures
• Linked List
• Binary Tree
• Binary Search Tree
• Segment Tree
• Disjoint Set Union
• Fenwick Tree
• Red-Black Tree
• Advanced Data Structures
• Graph Data Structure And Algorithms
• Introduction to Graphs - Data Structure and Algorithm Tutorials
• Graph and its representations
• Types of Graphs with Examples
• Basic Properties of a Graph
• Applications, Advantages and Disadvantages of Graph
• Transpose graph
• Difference Between Graph and Tree

BFS and DFS on Graph

• Breadth First Search or BFS for a Graph
• Depth First Search or DFS for a Graph
• Applications, Advantages and Disadvantages of Depth First Search (DFS)
• Applications, Advantages and Disadvantages of Breadth First Search (BFS)
• Iterative Depth First Traversal of Graph
• BFS for Disconnected Graph
• Transitive Closure of a Graph using DFS
• Difference between BFS and DFS

Cycle in a Graph

• Detect Cycle in a Directed Graph
• Detect cycle in an undirected graph
• Detect Cycle in a directed graph using colors
• Detect a negative cycle in a Graph | (Bellman Ford)
• Cycles of length n in an undirected and connected graph
• Detecting negative cycle using Floyd Warshall
• Clone a Directed Acyclic Graph

Shortest Paths in Graph

• How to find Shortest Paths from Source to all Vertices using Dijkstra's Algorithm
• Bellman–Ford Algorithm
• Floyd Warshall Algorithm
• Johnson's algorithm for All-pairs shortest paths
• Shortest Path in Directed Acyclic Graph
• Multistage Graph (Shortest Path)
• Shortest path in an unweighted graph
• Karp's minimum mean (or average) weight cycle algorithm
• 0-1 BFS (Shortest Path in a Binary Weight Graph)
• Find minimum weight cycle in an undirected graph

Minimum Spanning Tree in Graph

• Kruskal’s Minimum Spanning Tree (MST) Algorithm
• Difference between Prim's and Kruskal's algorithm for MST
• Applications of Minimum Spanning Tree
• Total number of Spanning Trees in a Graph
• Minimum Product Spanning Tree
• Reverse Delete Algorithm for Minimum Spanning Tree

Topological Sorting in Graph

• Topological Sorting
• All Topological Sorts of a Directed Acyclic Graph
• Kahn's algorithm for Topological Sorting
• Maximum edges that can be added to DAG so that it remains DAG
• Longest Path in a Directed Acyclic Graph
• Topological Sort of a graph using departure time of vertex

Connectivity of Graph

• Articulation Points (or Cut Vertices) in a Graph
• Biconnected Components
• Bridges in a graph
• Eulerian path and circuit for undirected graph
• Fleury's Algorithm for printing Eulerian Path or Circuit
• Strongly Connected Components
• Count all possible walks from a source to a destination with exactly k edges
• Euler Circuit in a Directed Graph
• Word Ladder (Length of shortest chain to reach a target word)
• Find if an array of strings can be chained to form a circle | Set 1
• Tarjan's Algorithm to find Strongly Connected Components
• Paths to travel each nodes using each edge (Seven Bridges of Königsberg)
• Dynamic Connectivity | Set 1 (Incremental)

Maximum flow in a Graph

• Max Flow Problem Introduction
• Ford-Fulkerson Algorithm for Maximum Flow Problem
• Find maximum number of edge disjoint paths between two vertices
• Find minimum s-t cut in a flow network
• Maximum Bipartite Matching
• Channel Assignment Problem
• Introduction to Push Relabel Algorithm
• Introduction and implementation of Karger's algorithm for Minimum Cut
• Dinic's algorithm for Maximum Flow

Some must do problems on Graph

• Find size of the largest region in Boolean Matrix
• Count number of trees in a forest
• A Peterson Graph Problem
• Clone an Undirected Graph
• Introduction to Graph Coloring

Traveling Salesman Problem (TSP) Implementation

• Introduction and Approximate Solution for Vertex Cover Problem
• Erdos Renyl Model (for generating Random Graphs)
• Chinese Postman or Route Inspection | Set 1 (introduction)
• Hierholzer's Algorithm for directed graph
• Boggle (Find all possible words in a board of characters) | Set 1
• Hopcroft–Karp Algorithm for Maximum Matching | Set 1 (Introduction)
• Construct a graph from given degrees of all vertices
• Determine whether a universal sink exists in a directed graph
• Number of sink nodes in a graph
• Two Clique Problem (Check if Graph can be divided in two Cliques)

Travelling Salesman Problem (TSP) : Given a set of cities and distances between every pair of cities, the problem is to find the shortest possible route that visits every city exactly once and returns to the starting point.  Note the difference between Hamiltonian Cycle and TSP. The Hamiltonian cycle problem is to find if there exists a tour that visits every city exactly once. Here we know that Hamiltonian Tour exists (because the graph is complete) and in fact, many such tours exist, the problem is to find a minimum weight Hamiltonian Cycle.  For example, consider the graph shown in the figure on the right side. A TSP tour in the graph is 1-2-4-3-1. The cost of the tour is 10+25+30+15 which is 80. The problem is a famous NP-hard problem. There is no polynomial-time known solution for this problem.   

Examples: 

In this post, the implementation of a simple solution is discussed.

• Consider city 1 as the starting and ending point. Since the route is cyclic, we can consider any point as a starting point.
• Generate all (n-1)! permutations of cities.
• Calculate the cost of every permutation and keep track of the minimum cost permutation.
• Return the permutation with minimum cost.

Below is the implementation of the above idea 

Time complexity:  O(n!) where n is the number of vertices in the graph. This is because the algorithm uses the next_permutation function which generates all the possible permutations of the vertex set.  Auxiliary Space: O(n) as we are using a vector to store all the vertices.

Please Login to comment...

Similar reads.

• NP Complete

Improve your Coding Skills with Practice

What kind of Experience do you want to share?

Ensure that you are logged in and have the required permissions to access the test.

A server error has occurred. Please refresh the page or try after some time.

An error has occurred. Please refresh the page or try after some time.

Signup and get free access to 100+ Tutorials and Practice Problems Start Now

• Linear Search
• Binary Search
• Ternary Search
• Bubble Sort
• Selection Sort
• Insertion Sort
• Counting Sort
• Bucket Sort
• Basics of Greedy Algorithms
• Graph Representation
• Breadth First Search
• Depth First Search
• Minimum Spanning Tree
• Shortest Path Algorithms
• Flood-fill Algorithm
• Articulation Points and Bridges
• Biconnected Components
• Strongly Connected Components
• Topological Sort
• Hamiltonian Path
• Maximum flow
• Minimum Cost Maximum Flow
• Basics of String Manipulation
• String Searching
• Z Algorithm
• Manachar’s Algorithm
• Introduction to Dynamic Programming 1
• 2 Dimensional
• State space reduction

Dynamic Programming and Bit Masking

First thing to make sure before using bitmasks for solving a problem is that it must be having small constraints, as solutions which use bitmasking generally take up exponential time and memory.

Let's first try to understand what Bitmask means. Mask in Bitmask means hiding something. Bitmask is nothing but a binary number that represents something. Let's take an example. Consider the set $$A = \{1, 2, 3, 4, 5\}$$. We can represent any subset of $$A$$ using a bitmask of length $$5$$, with an assumption that if $$i^{th} ( 0 \le i \le 4)$$ bit is set then it means $$i^{th}$$ element is present in subset. So the bitmask $$01010$$ represents the subset $$\{2, 4\}$$

Now the benefit of using bitmask. We can set the $$i^{th}$$ bit, unset the $$i^{th}$$ bit, check if $$i^{th}$$ bit is set in just one step each. Let's say the bitmask, $$b = 01010$$.

Set the $$i^{th}$$ bit : $$b | (1 \lt\lt i)$$. Let $$i = 0$$, so, $$$(1 \lt\lt i) = 00001$$$ $$$01010 | 00001 = 01011$$$ So now the subset includes the $$0^{th}$$ element also, so the subset is $$\{1, 2, 4\}$$.

Unset the $$i^{th}$$ bit : $$b \& !(1 \lt\lt i)$$. Let $$i=1$$, so, $$$(1 \lt\lt i) = 00010$$$ $$$!(1 \lt\lt i) = 11101$$$ $$$01010 \& 11101 = 01000$$$ Now the subset does not include the $$1^{st}$$ element, so the subset is $$\{4\}$$.

Check if $$i^{th}$$ bit is set : $$b \& (1 \lt\lt i)$$, doing this operation, if $$i^{th}$$ bit is set, we get a non zero integer otherwise, we get zero. Let $$ i = 3$$ $$$(1 \lt\lt i) = 01000$$$ $$$01010 \& 01000 = 01000$$$ Clearly the result is non-zero, so that means $$3^{rd}$$ element is present in the subset.

Let's take a problem, given a set, count how many subsets have sum of elements greater than or equal to a given value.

Algorithm is simple:

To iterate over all the subsets we are going to each number from 0 to 2 set_size -1 The above problem simply uses bitmask and complexity is O(2 n n).

Now, let's take another problem that uses dynamic programming along with bitmasks.

Assignment Problem: There are $$N$$ persons and $$N$$ tasks, each task is to be alloted to a single person. We are also given a matrix $$cost$$ of size $$N \times N$$, where $$cost[i][j]$$ denotes, how much person $$i$$ is going to charge for task $$j$$. Now we need to assign each task to a person in such a way that the total cost is minimum. Note that each task is to be alloted to a single person, and each person will be alloted only one task.

The brute force approach here is to try every possible assignment. Algorithm is given below:

Let's try to improve it using dynamic programming. Suppose the state of $$dp$$ is $$(k, mask)$$, where $$k$$ represents that person $$0$$ to $$k-1$$ have been assigned a task, and $$mask$$ is a binary number, whose $$i^{th}$$ bit represents if the $$i^{th}$$ task has been assigned or not. Now, suppose, we have $$answer(k, mask)$$, we can assign a task $$i$$ to person $$k$$, iff $$i^{th}$$ task is not yet assigned to any peron i.e. $$mask\&(1 \lt\lt i) = 0$$ then, $$answer(k+1, mask|(1 \lt\lt i)$$ will be given as: $$$answer(k+1, mask|(1 \lt\lt i)) = min(answer(k+1, mask|(1 \lt\lt i)), answer(k,mask)+cost[k][i]) $$$

One thing to note here is $$k$$ is always equal to the number set bits in $$mask$$, so we can remove that. So the dp state now is just $$(mask)$$, and if we have $$answer(mask)$$, then

$$$answer(mask|(1 \lt\lt i)) = min(answer(mask|(1 \lt\lt i)), answer(mask)+cost[x][i]) $$$ here $$x = $$number of set bits in $$mask$$. Complete algorithm is given below:

• An alphabet
• A special character
• Minimum 8 characters

A password reset link will be sent to the following email id

• Interview Q

DAA Tutorial

Asymptotic analysis, analysis of sorting, divide and conquer, lower bound theory, sorting in linear time, binary search trees, red black tree, dynamic programming, greedy algorithm, backtracking, shortest path, all-pairs shortest paths, maximum flow, sorting networks, complexity theory, approximation algo, string matching.

Interview Questions

• Send your Feedback to [email protected]

Help Others, Please Share

Learn Latest Tutorials

Transact-SQL

Reinforcement Learning

R Programming

React Native

Python Design Patterns

Python Pillow

Python Turtle

Preparation

Verbal Ability

Company Questions

Trending Technologies

Artificial Intelligence

Cloud Computing

Data Science

Machine Learning

B.Tech / MCA

Data Structures

Operating System

Computer Network

Compiler Design

Computer Organization

Discrete Mathematics

Ethical Hacking

Computer Graphics

Software Engineering

Web Technology

Cyber Security

C Programming

Control System

Data Mining

Data Warehouse