travelling salesperson problem using least cost branch and bound

• Interview Q

DAA Tutorial

Asymptotic analysis, analysis of sorting, divide and conquer, lower bound theory, sorting in linear time, binary search trees, red black tree, dynamic programming, greedy algorithm, backtracking, shortest path, all-pairs shortest paths, maximum flow, sorting networks, complexity theory, approximation algo, string matching.

Interview Questions

• Send your Feedback to [email protected]

Help Others, Please Share

Learn Latest Tutorials

Transact-SQL

Reinforcement Learning

R Programming

React Native

Python Design Patterns

Python Pillow

Python Turtle

Preparation

Verbal Ability

Company Questions

Trending Technologies

Artificial Intelligence

Cloud Computing

Data Science

Machine Learning

B.Tech / MCA

Data Structures

Operating System

Computer Network

Compiler Design

Computer Organization

Discrete Mathematics

Ethical Hacking

Computer Graphics

Software Engineering

Web Technology

Cyber Security

C Programming

Control System

Data Mining

Data Warehouse

Ace your Coding Interview

• DSA Problems
• Binary Tree
• Binary Search Tree
• Dynamic Programming
• Divide and Conquer
• Linked List
• Backtracking

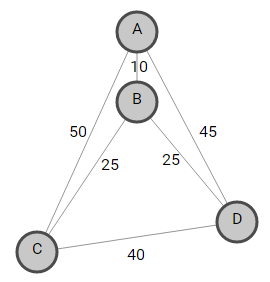
Travelling Salesman Problem using Branch and Bound

Given a set of cities and the distance between every pair of cities, the problem is to find the shortest possible route that visits every city exactly once and returns to the starting point.

For example, consider the following graph . A TSP tour in the graph is A —> B —> C —> D —> B —> A . The cost of the tour is 10 + 25 + 40 + 25 + 10 = 100 .

This post discusses the Travelling Salesman Problem using Branch and Bound.

  The term Branch and Bound refer to all state-space search methods in which all the children of an E–node are generated before any other live node can become the E–node. E–node is the node, which is being expended. State–space tree can be expended in any method, i.e., BFS or DFS . Both start with the root node and generate other nodes. A node that has been generated and whose children are not yet been expanded is called a live-node. A node is called a dead node, which has been generated, but it cannot be expanded further. In this method, we expand the most promising node, which means the node which promises that expanding or choosing it will give us the optimal solution. So, we prepare the tree starting from the root and then expand it.

We have a cost matrix defined by:

For example, consider the following cost matrix M ,

Following is the state-space tree for the above TSP problem, which shows the optimal solution marked in green:

As we can see from the above diagram, every node has a cost associated with it. When we go from the city i to city j , the cost of a node j will be the sum of the parent node i , the cost of an edge (i, j) , and the lower bound of the path starting at node j .

As the root node is the first node to be expanded, it doesn’t have any parent. So, the cost will be only the lower bound of the path starting at the root.

Now, how do we calculate the lower bound of the path starting at any node?

In general, to get the lower bound of the path starting from the node, we reduce each row and column so that there must be at least one zero in each row and Column. We need to reduce the minimum value from each element in each row and column.

Let’s start from the root node.

We reduce the minimum value in each row from each element in that row. The minimum in each row of cost matrix M is marked by blue [10 2 2 3 4] below.

After reducing the row, we get the below reduced matrix.

We then reduce the minimum value in each column from each element in that column. Minimum in each column is marked by blue [1 0 3 0 0] . After reducing the column, we get below the reduced matrix. This matrix will be further processed by child nodes of the root node to calculate their lower bound.

The total expected cost at the root node is the sum of all reductions.

Since we have discovered the root node C0 , the next node to be expanded can be any node from C1 , C2 , C3 , C4 . Whichever node has a minimum cost will be expanded further. So, we have to find out the expanding cost of each node.

The parent node C0 has below reduced matrix:

Let’s consider an edge from 0 —> 1 .

1. As we add an edge (0, 1) to our search space, set outgoing edges for city 0 to INFINITY and all incoming edges to city 1 to INFINITY . We also set (1, 0) to INFINITY .

So in a reduced matrix of the parent node, change all the elements in row 0 and column 1 and at index (1, 0) to INFINITY (marked in red).

The resulting cost matrix is:

2. We try to calculate the lower bound of the path starting at node 1 using the above resulting cost matrix. The lower bound is 0 as the matrix is already in reduced form, i.e., all rows and all columns have zero value.

Therefore, for node 1, the cost will be:

Let’s consider an edge from 0 —> 2

1. Change all the elements in row 0 and column 2 and at index (2, 0) to INFINITY (marked in red).

2. Now calculate the lower bound of the path starting at node 2 using the approach discussed earlier. The resultant matrix will be:

Therefore, for node 2, the cost will be

Let’s consider an edge from 0 —> 3 .

1. Change all the elements in row 0 and column 3 and at index (3, 0) to INFINITY (marked in red).

2. Now calculate the lower bound of the path starting at node 3 using the approach discussed earlier. The lower bound of the path starting at node 3 is 0 as it is already in reduced form, i.e., all rows and all columns have zero value.

Therefore, for node 3, the cost will be

Similarly, we calculate the cost of 0 —> 4 . Its cost will be 31 .

Now find a live node with the least estimated cost. Live nodes 1 , 2 , 3 , and 4 have costs 35 , 53 , 25 , and 31 , respectively. The minimum among them is node 3 , having cost 25 . So, node 3 will be expanded further, as shown in the state-space tree diagram. After adding its children to the list of live nodes, find a live node with the least cost and expand it. Continue the search till a leaf is encountered in the space search tree. If a leaf is encountered, then the tour is completed, and we will return to the root node.

  Following is the C++ implementation of the above idea:

Download    Run Code

Output: 1 —> 3 3 —> 4 4 —> 2 2 —> 5 5 —> 1   Total cost is 34

  The proposed method, which uses Branch and Bound, is better because it prepares the matrices in different steps. At each step, the cost matrix is calculated. From the initial point, we know that what can be the minimum cost of the tour. The cost of the initial stages is not an exact cost, but it gives some idea because it is the approximated cost. At each step, it gives us a strong reason for which node we should travel the next and which one not. It gives this fact in terms of the cost of expanding a particular node.

  References:

1. https://www.seas.gwu.edu/~bell/csci212/Branch_and_Bound.pdf 2. http://research.ijcaonline.org/volume65/number5/pxc3885866.pdf

Find minimum path sum in a triangle-shaped matrix

Rate this post

Average rating 4.91 /5. Vote count: 104

No votes so far! Be the first to rate this post.

We are sorry that this post was not useful for you!

Tell us how we can improve this post?

Thanks for reading.

To share your code in the comments, please use our online compiler that supports C, C++, Java, Python, JavaScript, C#, PHP, and many more popular programming languages.

Like us? Refer us to your friends and support our growth. Happy coding :)

Search anything:

Travelling Salesman Problem using Branch and Bound approach

Algorithms graph algorithms branch and bound.

Open-Source Internship opportunity by OpenGenus for programmers. Apply now.

In this article we will briefly discuss about the travelling salesman problem and the branch and bound method to solve the same.

What is the problem statement ?

Travelling Salesman Problem is based on a real life scenario, where a salesman from a company has to start from his own city and visit all the assigned cities exactly once and return to his home till the end of the day. The exact problem statement goes like this, " Given a set of cities and distance between every pair of cities, the problem is to find the shortest possible route that visits every city exactly once and returns to the starting point. "

There are two important things to be cleared about in this problem statement,

• Visit every city exactly once
• Cover the shortest path

What is branch and bound ?

Before going into the details of the branch and bound method lets focus on some important terms for the same,

State Space Search Method - Remember the word sample space from the probability theory ? That was a set of all the possible sample outputs. In a similar way, state space means, a set of states that a problem can be in. The set of states forms a graph where two states are connected if there is an operation that can be performed to transform the first state into the second. In a lighter note, this is just a set of some objects, which has some properties/characteristics, like in this problem, we have a node, it has a cost associated to it. The entire state space can be represented as a tree known as state space tree, which has the root and the leaves as per the normal tree, which are interms the elements of the statespace having the given graph node and a cost associated to it.

E-node - Expanded node or E node is the node which is been expanded. As we know a tree can be expanded using both BFS(Bredth First Search) and DFS(Depth First Search),all the expanded nodes are known as E-nodes .

Live-node - A node which has been generated and all of whose children are not yet been expanded is called a live-node.

Dead-node - If a node can't be expanded further, it's known as a dead-node.

The word, Branch and Bound refers to all the state space search methods in which we generate the childern of all the expanded nodes, before making any live node as an expanded one. In this method, we find the most promising node and expand it. The term promising node means, choosing a node that can expand and give us an optimal solution. We start from the root and expand the tree untill unless we approach an optilmal (minimum cost in case of this problem) solution.

How to get the cost for each node in the state space tree ?

To get further in branch and bound, we need to find the cost at the nodes at first. The cost is found by using cost matrix reduction , in accordance with two accompanying steps row reduction & column reduction .

In general to get the optimal(lower bound in this problem) cost starting from the node, we reduce each row and column in such a way that there must be atleast one 0 in each row and column. For doing this, we just need to reduce the minimum value from each row and column.

For example, suppose we have a cost matrix as shown below,

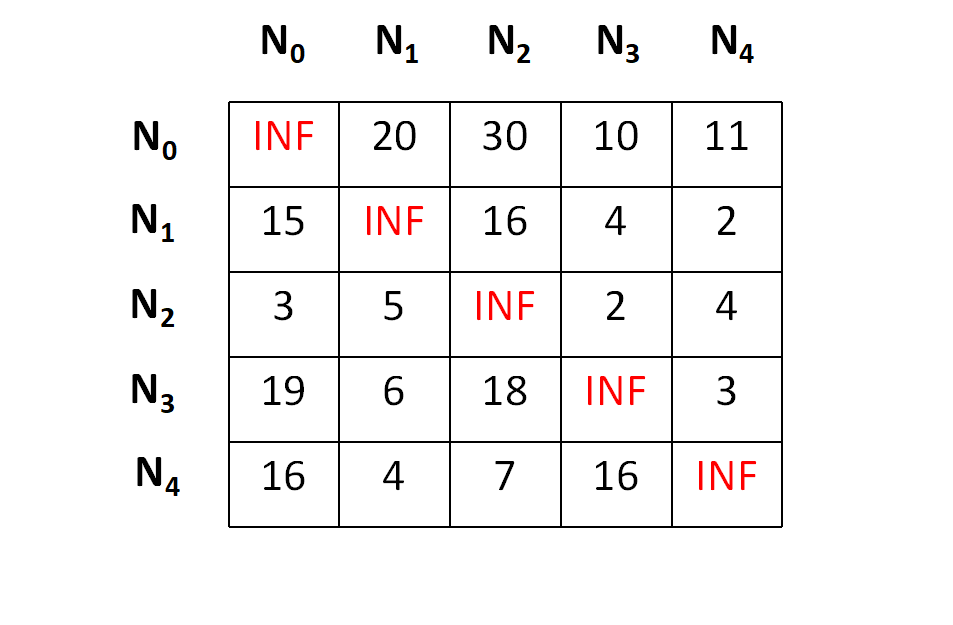
Let's start from node N0,;lets consider N0 as our first live node.

First of all we will perform the row operations and to do the same, we need to subtract the minimum value in each row from each element in that row. The minimums and the row reduced matrix is shown below,

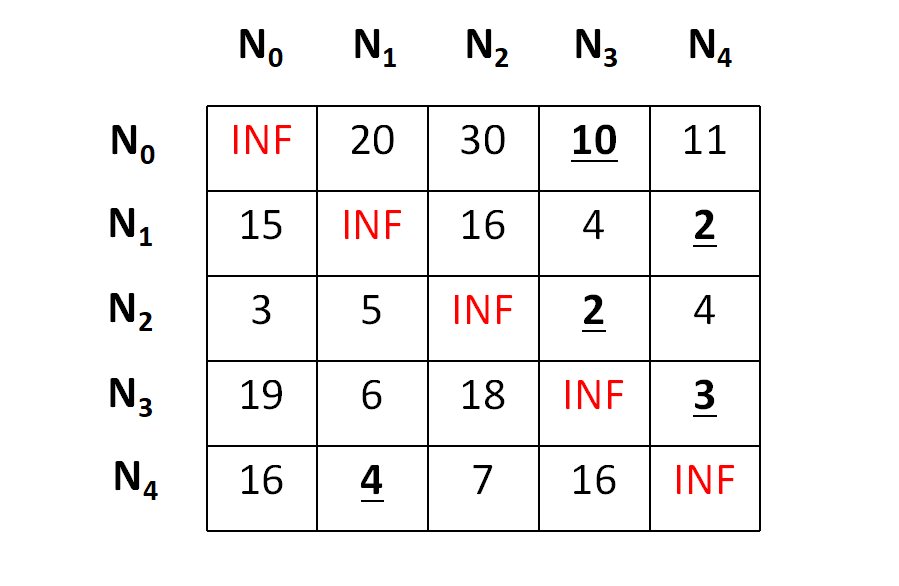
And after row reduction,

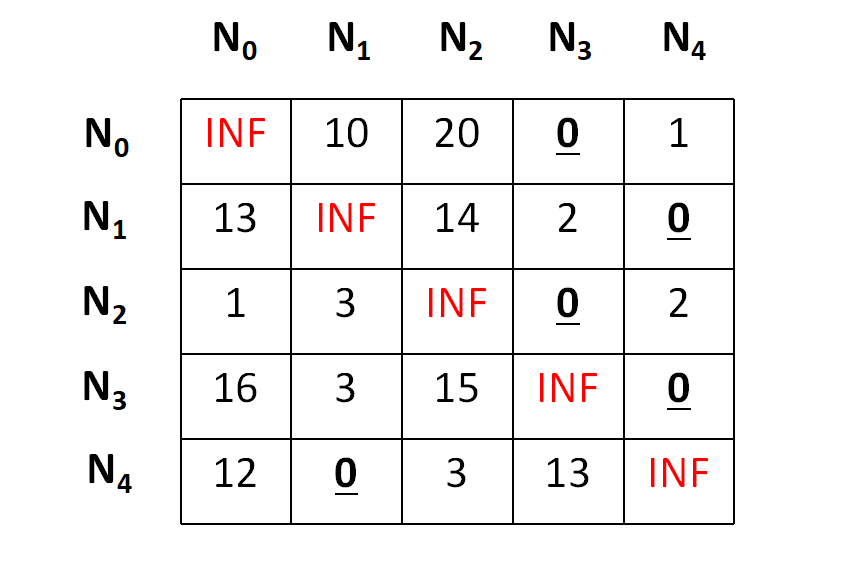
Now we need to perform the column operation in the same manner and we will get a final matrix as below,

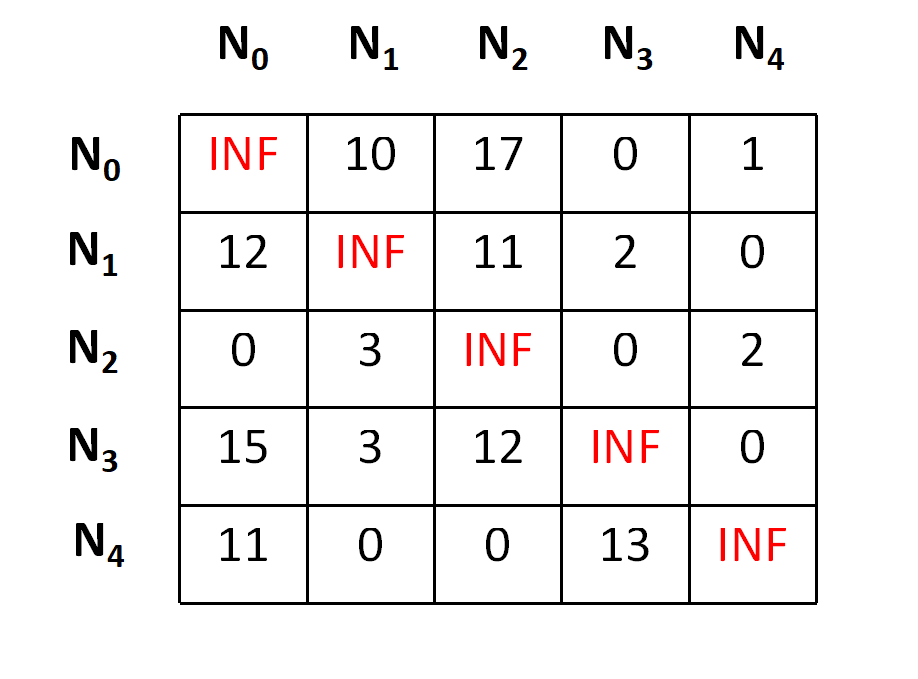
The total cost at any node is calculated by making a sum of all reductions, hence the cost for the node N0 can be depicted as,

cost = 10 + 2 + 2 + 3 + 4 + 1 + 3 = 25

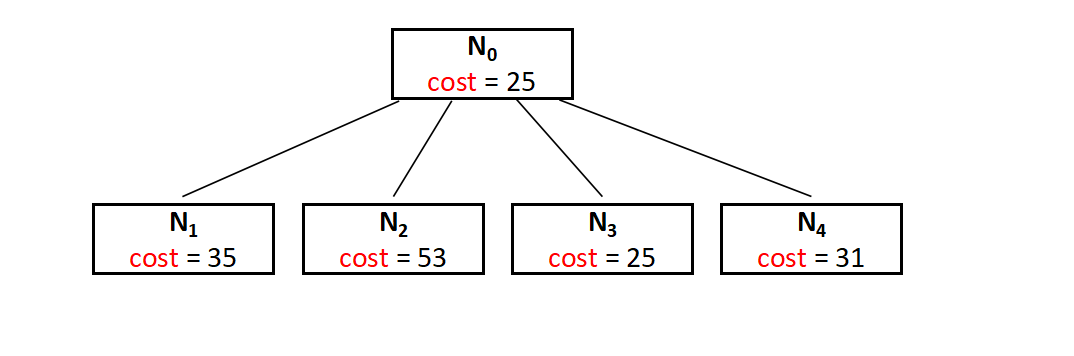
Now as we have founded the cost for the root node, it's the time for the expansion, and to do so, we have four more nodes namely, N1 , N2 , N3 , N4 .

Let's add the edge from N0 to N1 in our search space. To do so, we need to set outgoing routes for city N0 to INF as well as all incoming routes to city N1 to INF.Also we will set the (N0,N1) position of the cost matrix as INF. By doing so, we are just focusing on the cost of the node N1, that's an E-node. In an easier note, we have just forgotten that the graph has a N0 node, but we are focusing on something that the graph has been started from the N1 node. Following the transformation we have something as below,

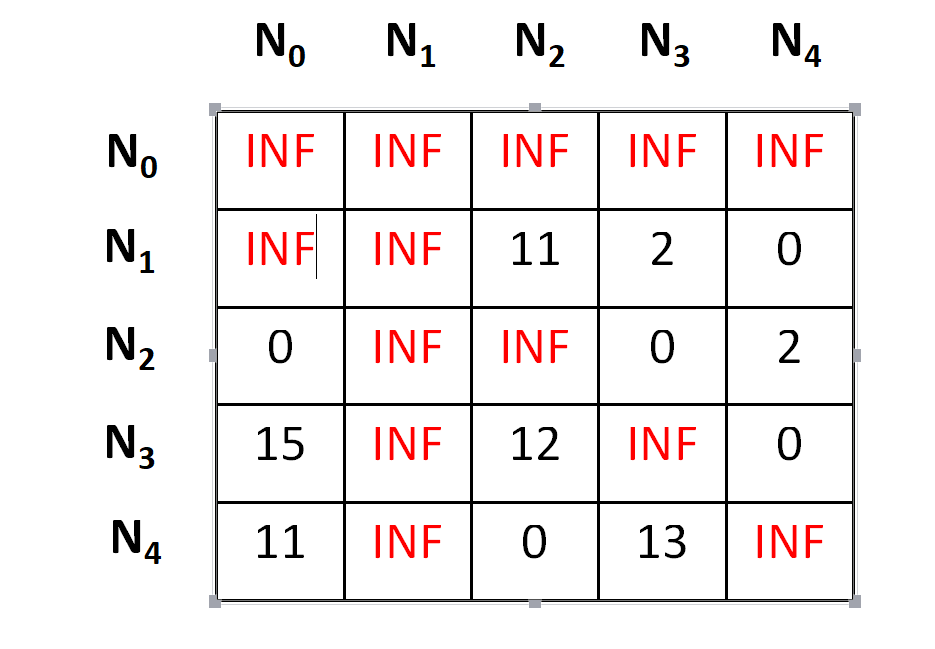
Now it's the time to repeat the lower bound finding(row-reduction and the column-reduction) part that we have performed earlier as well, following which we will get that the matrix is already in reduced form, i.e. all rows and all columns have zero value.

Now it's the time to calculate the cost.

cost = cost of node N0 + cost of the (N0,N1) position(before setting INF) + lower bound of the path starting at N1 = 25 + 10 + 0 = 35

Hence the cost for the E-Node N1 is 35. In a similar way we can find that, For N2 the cost is 53, For N3 the cost is 25, And for N4 the cost is 31.

Now we have a part of state space tree ready, whcih can be shown as below,

How to get towards the optimal solution ?

To get the optimal solution, we have to choose the next live node from the list of the extended nodes (E-nodes) and repeat the same procedure of extending the tree further by calculating the lower bound. Here in the partially built space search tree above we have the Node N3 as the node having the minimum cost and we can consider it as the live node and extend the tree further. This step is repeated until unless we find a dead node and can not extend the tree further. The cost of the dead node (leaf node) will be the answer. The entire space search tree can be drawn as follow,

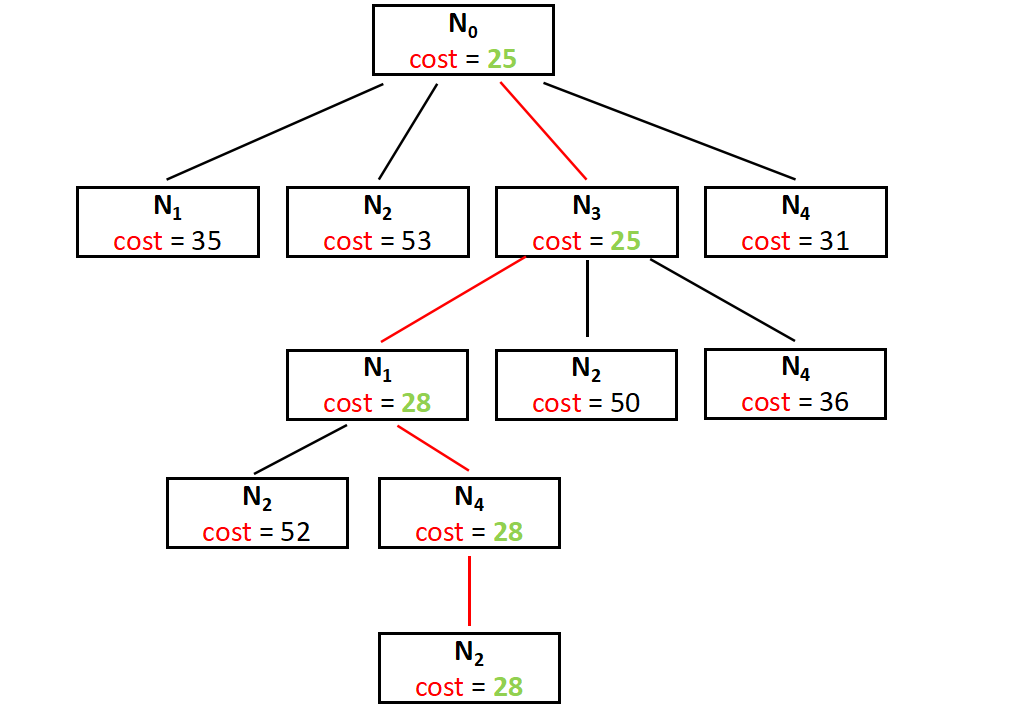
And the final cost is 28 , that's the minimum cost for a salesman to start from N0 and return to N0 by covering all the cities.

The Main Code

Now after knowing the entire process, this thing is easier to code. We have tried something new this time by attaching some more datastructures and objects to print the path as well. Have a look at the following code in order to understand it,

Code Explanation :

We would briefly go through the three main functions of the algorithm and try to understand how the algorithm is working, which is pretty similar to what we have learbed above.

reduce_row()

As the name suggests, this function is used to reduce the desired row. In this function we are using an awesome builtin function namely fill_n() available in the C++ STL. Have a look at the syntax,

This function makes it easy to fill an entire row with the desired value(INF here).

Now it's time to run two loops, one for the minimum value finding for each row and one for making the reduction. Have a look at the below snippet of the code.

You may guess the run time complexity of the above function is O(n^2) because the loop has two iterations embeded one inside the other. The run time complexity of the fill_n() function is Linear, i.e O(n) .

reduce_column()

As the name suggests, this function is used to reduce the desired column, in a similar fashion to what we have done above.

This function makes it easy to fill an entire column with the desired value(INF here).

cost_calculation()

This function need to get the reduced matrix as a parameter, perform the row reduction, the column reduction successively and then calculate the cost.

This can been seen below.

The time complexity of the program is O(n^2) as explained above for the row and column reduction functions.

What is the final time complexity ?

Now this thing is tricky and need a deeper understanding of what we are doing. We are actually creating all the possible extenstions of E-nodes in terms of tree nodes. Which is nothing but a permutation . Suppose we have N cities, then we need to generate all the permutations of the (N-1) cities, excluding the root city. Hence the time complexity for generating the permutation is O((n-1)!) , which is equal to O(2^(n-1)) .

Hence the final time complexity of the algorithm can be O(n^2 * 2^n) .

Fast Branch and Bound Algorithm for the Travelling Salesman Problem

• Conference paper
• First Online: 09 September 2016
• Cite this conference paper

• Radosław Grymin 14 &
• Szymon Jagiełło 14  

Part of the book series: Lecture Notes in Computer Science ((LNISA,volume 9842))

Included in the following conference series:

• IFIP International Conference on Computer Information Systems and Industrial Management

4151 Accesses

1 Citations

New strategies are proposed for implementing algorithms based on Branch and Bound scheme. Those include two minimal spanning tree lower bound modifications, a design based on the fact that edges in the optimal tour can never cross in the euclidean TSP and parallelization of Branch and Bound scheme. Proposed approaches are compared with primary algorithms.

You have full access to this open access chapter,  Download conference paper PDF

Similar content being viewed by others

Branch-and-Bound Algorithm for Symmetric Travelling Salesman Problem

Results for the close-enough traveling salesman problem with a branch-and-bound algorithm

A branch-and-cut algorithm for the balanced traveling salesman problem

• Branch-and-Bound
• Dynamic programming
• Parallel algorithm

1 Introduction

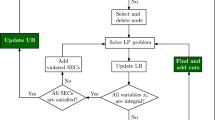
Branch and Bound (Branch and Bound, BnB, branch & bound) is an approach advised for designing exact algorithms solving \(\mathcal {NP}\) -hard combinatorial optimization and discrete problems. Branch and Bound was introduced by Land and Doig in 1960 [ 10 ]. Until the late 1970s, it was the state-of-the-art method for almost all big and complex problems that could not be solved by other techniques known at that time. And it is still used everywhere, where small improvement of solution leads to big rise in profits. Branch and Bound uses a tree search strategy to implicitly enumerate all possible solutions to a given problem, applying pruning rules to eliminate regions of the search space that cannot lead to a better solution [ 11 ].

In this article we are considering a minimization problem and the whole used terminology relates to it. In order to optimally solve the problem, Branch and Bound algorithm divides the whole set of solutions \(\mathcal {X}\) into mutually exclusive and exhaustive subsets \(\mathcal {X}_j\) , where \(j \in \mathcal {S} = \lbrace 1, 2, 3, \ldots , s \rbrace \) . In every moment of its work, algorithm stores the best found solution so far \(x_{\mathrm {ub}}\) and its value called upper bound and the set of subsets not yet analysed. Branch and Bound does not search these subsets to which it is assured that they do not contain optimal solution \(x^*\) , so it is much more effective than an exhaustive search. Decision, if some subset should be analysed or not, is based on its bound and objective function value counted for currently best found solution \(K(x_\mathrm {ub})\) . For minimization problem, such bound is called lower bound and it is lower or equal to all objective function values evaluated for every element of related subset. It is marked as LB . If for a certain subset, the lower bound is equal or greater than the value of the best solution found so far, such subset is removed from the set of subsets not yet analysed and will be no more considered. A good lower bound is a basic requirement for an efficient Branch and Bound minimization procedure [ 12 ].

The idea of Travelling Salesman Problem, TSP for short, relies in visiting every city by the sale representative from the given set of n cities exactly once [ 9 ], starting from and returning to the home city. In this article we are considering a symmetric TSP, where the distance between two cities is the same in each opposite direction. We also assume that there is a direct connection from each node to every other one. Formally, this problem is described as a search for the shortest Hamiltonian cycle [ 7 ] in the complete and symmetric graph \(\mathcal {K}_n = (\mathcal {V}_n, \mathcal {E}_n)\) containing \(n = |\mathcal {V}_n|\) nodes and \(m = |\mathcal {E}_n| = {{n}\atopwithdelims (){2}}\) edges. Nodes are numbered from 1 to n . We assume without loss of generality that the home city is the node with index number 1. Edge e , which connects nodes i and j , is marked as \(\lbrace i,j \rbrace \) or \(\lbrace j, i \rbrace \) and their distances are stored in the distance matrix \(D_n\) .

Branch and Bound algorithm for TSP constructs solutions by visiting cities. On each step there may be more than one remaining city to visit. The process of constructing solutions can be presented as a decision tree. Each node in such tree refers to a subset of the solution set and a lower bound can be established for it. Branch and Bound algorithm creates solutions by exploring such tree. It will not visit these nodes of the decision tree, for which it has certainty that it will not lead to the optimal solution.

The role of parallel algorithms in solving NP-hard problems significantly increased in the last decade. Bożejko proposed an improvement for speeding up the process of solving a single machine scheduling problem with total tardiness cost function by parallelization of generation of paths [ 2 ], a parallel genetic algorithm for the flow shop scheduling problem [ 4 ] and a method for solving permutational routing problems by population-based metaheuristics [ 5 ]. The same author designed new parallel objective function determination methods for the job shop scheduling [ 3 ] and flow shop [ 1 ] problems. Jagiełło and Żelazny proposed a parallel cost function approach for the Distance Constrained Vehicle Routing Problem which was designed to work on Graphics Processing Units (GPUs) [ 8 ]. In this paper we propose a parallel Branch and Bound design for the TSP problem.

2 Lower Bounds

The lower bound \(LB(\mathcal {X}_j)\) for a given node in the decision tree (that reflects to a certain set of solutions  \(\mathcal {X}_j\) ) is evaluated as a sum of the travelled distance \(MIL(\mathcal {X}_j)\) and the lower estimation of the remaining distance \(LE(\mathcal {X}_j)\) ,

It should be noted, when the travelling salesman visited k cities, the remaining way is a Hamiltonian path starting from the last visited city, that visits every city not visited so far and returning to the home city. It is showed in Fig.  1 .

Searched Hamiltonian cycle. The tour that has to be passed is marked by the dashed line.

The lower estimation estimates from the bottom an overall length of such shortest Hamiltonian path. This path is described by the following properties:

it does not visit already visited k nodes,

each node of the considered graph is visited only once,

there exists a subpath linking every two nodes of the considered graph,

it assumes beginning and ending node,

if the number of not visited cities is greater than one and travelling salesman is not currently in the home city, he cannot directly pass the way from the current city to some not visited city and immediately return to the home city,

it is built from \(n-k+1\) edges,

the first and the last city of the Hamiltonian path are connected with only one city.

By the relaxation of above constraints, we get lower estimation of the remaining distance \(LE(\mathcal {X}_j)\) . The weaker relaxation, the greater value of the lower estimation and it leads to better lower estimation (that rejects more solutions).

The Total Length of the Shortest Feasible Connections. The weakest and the most simple lower estimation LE of the remaining distance is obtained by counting the total length of the shortest not visited edges. It satisfies the constraints (a) and (b). Relaxation of constraints involves removal of constraints (b), (c), (d), (e), (f) and (g).

In order to evaluate the lower estimation , the distances associated with the inaccessible connections are removed from the weight matrix. Firstly, zeros from the main diagonal are removed. If the travelling salesman comes out from the city i , the numbers in the row with index i should be removed from the weight matrix. Afterwards, if travelling salesman enters the city with index j and it is not a home city, then from the weight matrix, values from the column j are removed. Moreover, if city with index j is not a second last one (such city, after which travelling salesman returns to the home city), value \(d_{j1}\) must be removed from the weight matrix. We determine the number of the remaining connections r that have to be passed as

where n is the number of all cities and k is the number of visited cities.

Values that were not removed from the weight matrix are sorted in the non-decreasing order and form a finite sequence \((a_n)\) . The sum of the first r values is the lower estimation of the remaining distance. Then, the lower bound can be computed from ( 1 ).

The Weight of the Minimum Spanning Tree. In this case, the lower estimation of the remaining distance LE and the lower bound is equal to the weight of the minimum spanning tree for the complete sub-graph that consists of the city where actually the travelling salesman is located \(x_k\) , not having visited cities so far \(\left\{ x_{k+1}, x_{k+2}, x_{k+3}, \ldots , x_n \right\} \) and the home city \(x_1 = 1\) . It satisfies the constraints (a), (c) and (f). Relaxation involves removal of the constraints (b), (d), (e) and (g). In order to evaluate the minimum spanning tree weight, Prim’s algorithm is used. When the weight of the minimum spanning tree is computed (and it is also a value of the lower estimation LE ), ( 1 ) will be used to determine the lower bound .

The Weight of the Minimum Spanning Tree – 1st Modification. Algorithm was proposed by Mariusz Makuchowski from Department of Control Systems and Mechatronics of Wrocław University of Science and Technology (personal communication, November 3, 2014). The lower estimation of the remaining distance is evaluated as a sum of minimum spanning tree weight for graph consisting of the cities not having been visited so far \(\left\{ x_{k+1}, x_{k+2}, x_{k+3}, \ldots , x_n \right\} \) and the home city \(x_1 = 1\) and the sum of weights of two shortest edges connecting the home city with nearest not visited edge and the current city with nearest not visited edge. If travelling salesman is currently in the home city, lower estimation is counted as a sum of the weight of minimal spanning tree in the graph containing not visited cities and doubled distance from the home city to the nearest not visited node. It satisfies the constraints (a), (c), (f) and (g). Relaxation involves removal of the constraints (b), (d) and (e).

The Weight of the Minimum Spanning Tree – 2nd Modification. It is the improved version of the previous algorithm. The lower estimation of the remaining distance is evaluated as a sum of minimum spanning tree weight for graph consisting of not visited cities \(\left\{ x_{k+1}, x_{k+2}, x_{k+3}, \ldots , x_n \right\} \) and the sum of two weights of edges connecting the home city and the current city with not visited cities (and these cities must be different). If the travelling salesman is currently in the home city, the lower estimation is a sum of weight of the minimum spanning tree in graph containing not visited cities and the sum of two weights of shortest edges connecting home city with different not visited cities so far. It satisfies constraints (a), (c), (e), (f) and (g). Relaxation involves removal of constraints (b) and (d).

3 Priority of Analysed Sets

The order in which the algorithm searches the decision tree is very important. The size of the priority queue will grow fast if leaves are rarely visited and new upper bounds will not be found. The algorithm must have a tendency to search the graph towards leaves. By assigning a priority to sets stored in the priority queue we control the way the algorithm will search the decision tree.

We chose the following way of counting priority that promotes subsets with the lowest increase of lower bound

where P , AI , LB and k denote the subsets priority in the queue, the mean increase of the lower bound, the lower bound and the number of visited cities accordingly.

4 Parallel Branch and Bound Algorithm

In the parallel algorithm we use a pool approach with arbitrary fixed number of processes. It means that program executes in several processes and one of them will be called supervisory process and the rest will be called worker processes (see Fig.  2 ). In the initialization phase, supervisory process reads the instance data from the TSPLIB file, generates the weight matrix and distributes it to all worker processes . It also establishes the best solution found so far and the upper bound by running 2-opt algorithm on the result of the nearest neighbour algorithm. It stores the priority queue of solution sets not analysed so far and the best solution so far.

During computation phase, if some worker process notifies the supervisory process about its idle state via WORKER_FINISHED_TASK message and if there are still some solutions sets to be analysed in the priority queue, the supervisory process pops the first solution set with the highest priority and sends it to the worker process via PERFORM_TASK_REQ message and stores the information that the process is performing task. Algorithm stops when there are no more sets in the priority queue to analyse and if all worker processes informed supervisory process that they finished analysing task by sending WORKER_FINISHED_TASK .

Each worker process stores the upper bound value. If some worker process found a solution with the objective function value smaller than the upper bound, it sends this solution with upper bound update proposal to the supervisory process in UPPER_BOUND message. The supervisory process checks if the proposed upper bound value is better than the currently stored one. If it is true, the new best solution so far and the new upper bound value are stored in the supervisory process , the new upper bound value is distributed to all worker processes in the UPPER_BOUND message except one which found it and all subsets with the lower bound greater than the new upper bound are removed from the priority queue. Otherwise, the new proposed upper bound value is discarded. Such check is important in a situation when two workers find better solutions (with different objective function values) than the best solution found so far and simultaneously send proposal to the supervisory process for changing the best solution found so far and the upper bound. If the supervisory process obtains upper bound with smaller value first, it will update upper bound and when it obtains one with greater value, second upper bound value change proposal will be discarded after the check.

Sequence diagram that describes solving TSP by the Parallel Branch and Bound algorithm. The initialization part of algorithm was omitted.

Worker processes divide set obtained in the PERFORM_TASK_REQ message into subsets. If the subset has only one element it means that the worker found a solution. Otherwise, if obtained subsets contains more than one element, it calculates lower bounds for them. On the basis of the lower bound and the upper bound it is established if the optimal solution can belong to the obtained subset. If it is true, the subset is send back to the supervisory process via TASK_PUSH_REQ .

5 Intersections in Euclidean TSP

The edges in an optimal tour can never cross in an euclidean TSP. If edges \(\lbrace i,k \rbrace \) and \(\lbrace j,l \rbrace \) did cross, they would constitute the diagonals of a quadrilateral \(\lbrace i,j,k,l \rbrace \) and could profitably be replaced by a pair of opposite sides [ 6 ]. Instances for which all points are located on the same line are the only exceptions. Based on that fact two algorithms were proposed. The first one is a modification of the Brute force method the second is an adjustment of the Branch and Bound ( Branch and Cut ) approach. Before adding an edge to the current sub-tour it is probed for crossings with any of the edges of the current sub-tour. If an intersection occurs, the edge will not be added, thus the whole branch will be omitted.

Execution time for random data ( \(log_{10}\) scale)

6 Computational Experiments

The experiments were performed on a machine equipped with an Intel X980 CPU (6 physical cores), 24 GB of RAM, GCC version 4.6.3 (Ubuntu/Linaro 4.6.3-1ubuntu5) and MPICH 1.4.1 (mpic++, mpirun). The execution time of the specified approaches was measured. The sequential algorithms put under test were:

Branch and Bound ( Branch and Cut ) with four different lower bound approaches and without and with intersection checking:

the shortest feasible connections (BB(sfc), BB(sfc,i)),

the minimum spanning tree (BB(mst), BB(mst,i)),

the minimum spanning tree – 1st modification (BB(mstm), BB(mstm,i)),

the minimum spanning tree – 2nd modification (BB(mstg), BB(mstg,i)).

Bellman-Held-Karp dynamic algorithm (Bellman),

Brute force without and with intersections checking (BF, BF(i)).

For the reason that the algorithms were compared with Brute force method only small problem instances were used. TSPLIB contained only two benchmarks, which fulfilled this requirement: burma14 and ulysses16 . The results obtained from working with those data sets are presented in Table  1 .

It is quite interesting that the dynamic programming design performed so well as it performed best out of all algorithms for the ulysses16 data set. A single case is unfortunately not enough for accurate conclusions. Due to the small number of available benchmarks 7 random instances of sizes from 10 to 17 were generated. Function rand (stdlib) initialized with the seed 734834 was used to obtain x,y values from the range from 0 to 100. The results were presented in Table  2 and in Fig.  3 .

The BF method was not tested against the rand17 instance for the reason that the experiment would take too long (estimated 22 days). The results clearly indicate that the BF and BB algorithms benefit from checking intersections. The modified BB method was vastly faster than its basic version for each lower estimation. Even the BF(i) method has been proved to be working faster than the BB(sfc) algorithm. Both mst lower bound adjustments (1-Makuchowski, 2-Grymin) proved to be superior compared to the standard approach. As expected the dynamic programming technique operated faster than BB(sfc), BB(sfc,i), BF and BB(i) but slower than mst based BB designs ( rand10 is the only exception). The BB(mstg,i) method turned out to be the leading solution resulting in shortest execution times for each test instance. Instance size dependent speedup obtained in comparison to the BF, Bellman and BB(mst) algorithms is presented in Fig.  4 .

BB(mstg,i) speedup compared to selected algorithms for the burma14 benchmark ( \(log_{10}\) scale)

BB(mstg,i) speedup compared to selected algorithms ( \(log_{10}\) scale)

Parallel version of the leading approach was tested with the number of mpi processes in the range 2–12 and with the burma14 benchmark. The results were presented in Table  3 . It is shown that the mpi implementation utilizes all physical cores. Speedup is rising until the number of mpi processes equals 7 (1 supervisory process and 6 worker processes ). MPI processes count dependent speedup calculated in comparison to the sequential versions of the BF, Bellman and BB(mst) algorithms is presented in Fig.  5 . The maximum obtained speedup in comparison to the selected approaches is 38.318, 20.545 and 22755.273 accordingly.

7 Conclusion

Both proposed minimal spanning tree modifications proved to perform greatly faster than the base version. The intersections checking approach was successfully combined with Branch And Bound and Brute force designs and provided additional improvements. The Branch and Bound used with 2nd minimum spanning tree modification as lower estimation algorithm and combined with intersections checking mechanism turned out to be the best solution and achieved a massive speedup when compared to the Brute force, Bellman, and Branch and Bound used with standard minimal spanning tree algorithms. Additionally, its parallel version appeared to scale well and provided a further rise in performance.

Bożejko, W.: Solving the flow shop problem by parallel programming. J. Parallel Distrib. Comput. 69 , 470–481 (2009)

Article   Google Scholar  

Bożejko, W.: Parallel path relinking method for the single machine total weighted tardiness problem with sequence-dependent setups. J. Intell. Manuf. 21 , 777–785 (2010)

Bożejko, W.: On single-walk parallelization of the job shop problem solving algorithms. Comput. Oper. Res. 39 , 2258–2264 (2012)

Article   MathSciNet   Google Scholar  

Bożejko, W., Wodecki, M.: Parallel genetic algorithm for the flow shop scheduling problem. In: Wyrzykowski, R., Dongarra, J., Paprzycki, M., Waśniewski, J. (eds.) PPAM 2004. LNCS, vol. 3019, pp. 566–571. Springer, Heidelberg (2004)

Chapter   Google Scholar  

Bożejko, W., Wodecki, M.: Solving permutational routing problems by population-based metaheuristics. Comput. Ind. Eng. 57 (1), 269–276 (2009)

Cook, W.J.: In Pursuit of the Traveling Salesman: Mathematics at the Limits of Computation. Princeton University Press, Princeton (2012)

MATH   Google Scholar  

Feiring, B.: An efficient procedure for obtaining feasible solutions to the n-city traveling salesman problem. Math. Comput. Modell. 13 (3), 67–71 (1990)

Jagiełło, S., Żelazny, D.: Solving multi-criteria vehicle routing problem by parallel tabu search on GPU. Procedia Comput. Sci. 18 , 2529–2532 (2013)

Jünger, M., Rinaldi, G., Reinelt, G.: The traveling salesman problem. Handbooks Oper. Res. Manage. Sci. 7 , 225–330 (1995)

Land, A.H., Doig, A.G.: An automatic method of solving discrete programming problems. Econometrica: J. Econometric Soc. 28 , 497–520 (1960)

Morrison, D.R., Jacobson, S.H., Sauppe, J.J., Sewell, E.C.: Branch-and-Bound algorithms: a survey of recent advances in searching, branching, and pruning. Discrete Optim. 19 , 79–102 (2016)

Toffolo, T.A.M., Wauters, T., Malderen, S.V., Berghe, G.V.: Branch-and-Bound with decomposition-based lower bounds for the Traveling Umpire Problem. Eur. J. Oper. Res. 250 (3), 737–744 (2016)

Download references

Author information

Authors and affiliations.

Department of Control Systems and Mechatronics, Faculty of Electronics, Wrocław University of Science and Technology, Wrocław, Poland

Radosław Grymin & Szymon Jagiełło

You can also search for this author in PubMed   Google Scholar

Corresponding author

Correspondence to Radosław Grymin .

Editor information

Editors and affiliations.

Bialystok University of Technology , Bialystok, Poland

Khalid Saeed

University of Bialystok , Vilnius, Lithuania

Władysław Homenda

Rights and permissions

Open Access This chapter is licensed under the terms of the Creative Commons Attribution-NonCommercial 2.5 International License (http://creativecommons.org/licenses/by-nc/2.5/), which permits any noncommercial use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license and indicate if changes were made.

The images or other third party material in this chapter are included in the chapter's Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the chapter's Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder.

Reprints and permissions

Copyright information

© 2016 IFIP International Federation for Information Processing

About this paper

Cite this paper.

Grymin, R., Jagiełło, S. (2016). Fast Branch and Bound Algorithm for the Travelling Salesman Problem. In: Saeed, K., Homenda, W. (eds) Computer Information Systems and Industrial Management. CISIM 2016. Lecture Notes in Computer Science(), vol 9842. Springer, Cham. https://doi.org/10.1007/978-3-319-45378-1_19

Download citation

DOI : https://doi.org/10.1007/978-3-319-45378-1_19

Published : 09 September 2016

Publisher Name : Springer, Cham

Print ISBN : 978-3-319-45377-4

Online ISBN : 978-3-319-45378-1

eBook Packages : Computer Science Computer Science (R0)

Share this paper

Anyone you share the following link with will be able to read this content:

Sorry, a shareable link is not currently available for this article.

Provided by the Springer Nature SharedIt content-sharing initiative

• Publish with us

Policies and ethics

Societies and partnerships

• Find a journal
• Track your research

• Data Structures
• Linked List
• Binary Tree
• Binary Search Tree
• Segment Tree
• Disjoint Set Union
• Fenwick Tree
• Red-Black Tree
• Advanced Data Structures
• Graph Data Structure And Algorithms
• Introduction to Graphs - Data Structure and Algorithm Tutorials
• Graph and its representations
• Types of Graphs with Examples
• Basic Properties of a Graph
• Applications, Advantages and Disadvantages of Graph
• Transpose graph
• Difference Between Graph and Tree

BFS and DFS on Graph

• Breadth First Search or BFS for a Graph
• Depth First Search or DFS for a Graph
• Applications, Advantages and Disadvantages of Depth First Search (DFS)
• Applications, Advantages and Disadvantages of Breadth First Search (BFS)
• Iterative Depth First Traversal of Graph
• BFS for Disconnected Graph
• Transitive Closure of a Graph using DFS
• Difference between BFS and DFS

Cycle in a Graph

• Detect Cycle in a Directed Graph
• Detect cycle in an undirected graph
• Detect Cycle in a directed graph using colors
• Detect a negative cycle in a Graph | (Bellman Ford)
• Cycles of length n in an undirected and connected graph
• Detecting negative cycle using Floyd Warshall
• Clone a Directed Acyclic Graph

Shortest Paths in Graph

• How to find Shortest Paths from Source to all Vertices using Dijkstra's Algorithm
• Bellman–Ford Algorithm
• Floyd Warshall Algorithm
• Johnson's algorithm for All-pairs shortest paths
• Shortest Path in Directed Acyclic Graph
• Multistage Graph (Shortest Path)
• Shortest path in an unweighted graph
• Karp's minimum mean (or average) weight cycle algorithm
• 0-1 BFS (Shortest Path in a Binary Weight Graph)
• Find minimum weight cycle in an undirected graph

Minimum Spanning Tree in Graph

• Kruskal’s Minimum Spanning Tree (MST) Algorithm
• Difference between Prim's and Kruskal's algorithm for MST
• Applications of Minimum Spanning Tree
• Total number of Spanning Trees in a Graph
• Minimum Product Spanning Tree
• Reverse Delete Algorithm for Minimum Spanning Tree

Topological Sorting in Graph

• Topological Sorting
• All Topological Sorts of a Directed Acyclic Graph
• Kahn's algorithm for Topological Sorting
• Maximum edges that can be added to DAG so that it remains DAG
• Longest Path in a Directed Acyclic Graph
• Topological Sort of a graph using departure time of vertex

Connectivity of Graph

• Articulation Points (or Cut Vertices) in a Graph
• Biconnected Components
• Bridges in a graph
• Eulerian path and circuit for undirected graph
• Fleury's Algorithm for printing Eulerian Path or Circuit
• Strongly Connected Components
• Count all possible walks from a source to a destination with exactly k edges
• Euler Circuit in a Directed Graph
• Word Ladder (Length of shortest chain to reach a target word)
• Find if an array of strings can be chained to form a circle | Set 1
• Tarjan's Algorithm to find Strongly Connected Components
• Paths to travel each nodes using each edge (Seven Bridges of Königsberg)
• Dynamic Connectivity | Set 1 (Incremental)

Maximum flow in a Graph

• Max Flow Problem Introduction
• Ford-Fulkerson Algorithm for Maximum Flow Problem
• Find maximum number of edge disjoint paths between two vertices
• Find minimum s-t cut in a flow network
• Maximum Bipartite Matching
• Channel Assignment Problem
• Introduction to Push Relabel Algorithm
• Introduction and implementation of Karger's algorithm for Minimum Cut
• Dinic's algorithm for Maximum Flow

Some must do problems on Graph

• Find size of the largest region in Boolean Matrix
• Count number of trees in a forest
• A Peterson Graph Problem
• Clone an Undirected Graph
• Introduction to Graph Coloring

Traveling Salesman Problem (TSP) Implementation

• Introduction and Approximate Solution for Vertex Cover Problem
• Erdos Renyl Model (for generating Random Graphs)
• Chinese Postman or Route Inspection | Set 1 (introduction)
• Hierholzer's Algorithm for directed graph
• Boggle (Find all possible words in a board of characters) | Set 1
• Hopcroft–Karp Algorithm for Maximum Matching | Set 1 (Introduction)
• Construct a graph from given degrees of all vertices
• Determine whether a universal sink exists in a directed graph
• Number of sink nodes in a graph
• Two Clique Problem (Check if Graph can be divided in two Cliques)

Travelling Salesman Problem (TSP) : Given a set of cities and distances between every pair of cities, the problem is to find the shortest possible route that visits every city exactly once and returns to the starting point.  Note the difference between Hamiltonian Cycle and TSP. The Hamiltonian cycle problem is to find if there exists a tour that visits every city exactly once. Here we know that Hamiltonian Tour exists (because the graph is complete) and in fact, many such tours exist, the problem is to find a minimum weight Hamiltonian Cycle.  For example, consider the graph shown in the figure on the right side. A TSP tour in the graph is 1-2-4-3-1. The cost of the tour is 10+25+30+15 which is 80. The problem is a famous NP-hard problem. There is no polynomial-time known solution for this problem.   

Examples: 

In this post, the implementation of a simple solution is discussed.

• Consider city 1 as the starting and ending point. Since the route is cyclic, we can consider any point as a starting point.
• Generate all (n-1)! permutations of cities.
• Calculate the cost of every permutation and keep track of the minimum cost permutation.
• Return the permutation with minimum cost.

Below is the implementation of the above idea 

Time complexity:  O(n!) where n is the number of vertices in the graph. This is because the algorithm uses the next_permutation function which generates all the possible permutations of the vertex set.  Auxiliary Space: O(n) as we are using a vector to store all the vertices.

Please Login to comment...

Similar reads.

• NP Complete

Improve your Coding Skills with Practice

What kind of Experience do you want to share?

Navigation Menu

Search code, repositories, users, issues, pull requests..., provide feedback.

We read every piece of feedback, and take your input very seriously.

Saved searches

Use saved searches to filter your results more quickly.

To see all available qualifiers, see our documentation .

• Notifications

Traveling salesman problem using branch and bound algorithm

brielov/tsp

Folders and files, repository files navigation, traveling salesman problem.

This is my humble attempt of porting a C++ algorithm I found on the internet that solves the traveling salesman problem using the branch and bound algorithm.

First, you need a cost matrix, being a two dimensional array of distances between nodes.

Here, the output is a Node containing two valuable properties: path and cost .

The path property contain the indicies of the optimal/shortest route. The cost property is the total cost/distance of the tour.

Geolocation

For convenience, a geolocation helper is built into this library.

The first node is always the starting point, so you should put your point of departure first.

So, according to the result from above, the optimal tour would be:

And the cost would be around 46.544 kilometers

Code of conduct

• TypeScript 100.0%

• Data Structures & Algorithms
• DSA - Overview
• DSA - Environment Setup
• DSA - Algorithms Basics
• DSA - Asymptotic Analysis
• Data Structures
• DSA - Data Structure Basics
• DSA - Data Structures and Types
• DSA - Array Data Structure
• Linked Lists
• DSA - Linked List Data Structure
• DSA - Doubly Linked List Data Structure
• DSA - Circular Linked List Data Structure
• Stack & Queue
• DSA - Stack Data Structure
• DSA - Expression Parsing
• DSA - Queue Data Structure
• Searching Algorithms
• DSA - Searching Algorithms
• DSA - Linear Search Algorithm
• DSA - Binary Search Algorithm
• DSA - Interpolation Search
• DSA - Jump Search Algorithm
• DSA - Exponential Search
• DSA - Fibonacci Search
• DSA - Sublist Search
• DSA - Hash Table
• Sorting Algorithms
• DSA - Sorting Algorithms
• DSA - Bubble Sort Algorithm
• DSA - Insertion Sort Algorithm
• DSA - Selection Sort Algorithm
• DSA - Merge Sort Algorithm
• DSA - Shell Sort Algorithm
• DSA - Heap Sort
• DSA - Bucket Sort Algorithm
• DSA - Counting Sort Algorithm
• DSA - Radix Sort Algorithm
• DSA - Quick Sort Algorithm
• Graph Data Structure
• DSA - Graph Data Structure
• DSA - Depth First Traversal
• DSA - Breadth First Traversal
• DSA - Spanning Tree
• Tree Data Structure
• DSA - Tree Data Structure
• DSA - Tree Traversal
• DSA - Binary Search Tree
• DSA - AVL Tree
• DSA - Red Black Trees
• DSA - B Trees
• DSA - B+ Trees
• DSA - Splay Trees
• DSA - Tries
• DSA - Heap Data Structure
• DSA - Recursion Algorithms
• DSA - Tower of Hanoi Using Recursion
• DSA - Fibonacci Series Using Recursion
• Divide and Conquer
• DSA - Divide and Conquer
• DSA - Max-Min Problem
• DSA - Strassen's Matrix Multiplication
• DSA - Karatsuba Algorithm
• Greedy Algorithms
• DSA - Greedy Algorithms
• DSA - Travelling Salesman Problem (Greedy Approach)
• DSA - Prim's Minimal Spanning Tree
• DSA - Kruskal's Minimal Spanning Tree
• DSA - Dijkstra's Shortest Path Algorithm
• DSA - Map Colouring Algorithm
• DSA - Fractional Knapsack Problem
• DSA - Job Sequencing with Deadline
• DSA - Optimal Merge Pattern Algorithm
• Dynamic Programming
• DSA - Dynamic Programming
• DSA - Matrix Chain Multiplication
• DSA - Floyd Warshall Algorithm
• DSA - 0-1 Knapsack Problem
• DSA - Longest Common Subsequence Algorithm
• DSA - Travelling Salesman Problem (Dynamic Approach)
• Approximation Algorithms
• DSA - Approximation Algorithms
• DSA - Vertex Cover Algorithm
• DSA - Set Cover Problem
• DSA - Travelling Salesman Problem (Approximation Approach)
• Randomized Algorithms
• DSA - Randomized Algorithms
• DSA - Randomized Quick Sort Algorithm
• DSA - Karger’s Minimum Cut Algorithm
• DSA - Fisher-Yates Shuffle Algorithm
• DSA Useful Resources
• DSA - Questions and Answers
• DSA - Quick Guide
• DSA - Useful Resources
• DSA - Discussion
• Selected Reading
• UPSC IAS Exams Notes
• Developer's Best Practices
• Questions and Answers
• Effective Resume Writing
• HR Interview Questions
• Computer Glossary

Travelling Salesman Problem (Greedy Approach)

Travelling salesperson algorithm.

The travelling salesman problem is a graph computational problem where the salesman needs to visit all cities (represented using nodes in a graph) in a list just once and the distances (represented using edges in the graph) between all these cities are known. The solution that is needed to be found for this problem is the shortest possible route in which the salesman visits all the cities and returns to the origin city.

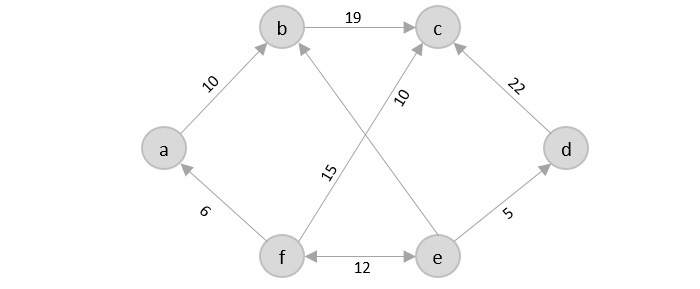
If you look at the graph below, considering that the salesman starts from the vertex ‘a’, they need to travel through all the remaining vertices b, c, d, e, f and get back to ‘a’ while making sure that the cost taken is minimum.

There are various approaches to find the solution to the travelling salesman problem: naive approach, greedy approach, dynamic programming approach, etc. In this tutorial we will be learning about solving travelling salesman problem using greedy approach.

As the definition for greedy approach states, we need to find the best optimal solution locally to figure out the global optimal solution. The inputs taken by the algorithm are the graph G {V, E}, where V is the set of vertices and E is the set of edges. The shortest path of graph G starting from one vertex returning to the same vertex is obtained as the output.

Travelling salesman problem takes a graph G {V, E} as an input and declare another graph as the output (say G’) which will record the path the salesman is going to take from one node to another.

The algorithm begins by sorting all the edges in the input graph G from the least distance to the largest distance.

The first edge selected is the edge with least distance, and one of the two vertices (say A and B) being the origin node (say A).

Then among the adjacent edges of the node other than the origin node (B), find the least cost edge and add it onto the output graph.

Continue the process with further nodes making sure there are no cycles in the output graph and the path reaches back to the origin node A.

However, if the origin is mentioned in the given problem, then the solution must always start from that node only. Let us look at some example problems to understand this better.

Consider the following graph with six cities and the distances between them −

From the given graph, since the origin is already mentioned, the solution must always start from that node. Among the edges leading from A, A → B has the shortest distance.

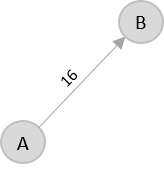
Then, B → C has the shortest and only edge between, therefore it is included in the output graph.

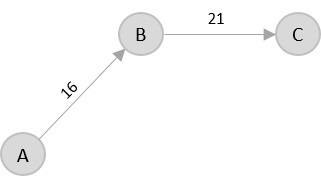
There’s only one edge between C → D, therefore it is added to the output graph.

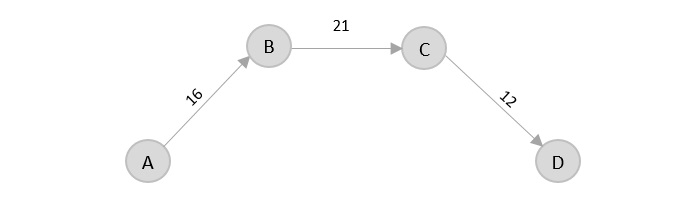
There’s two outward edges from D. Even though, D → B has lower distance than D → E, B is already visited once and it would form a cycle if added to the output graph. Therefore, D → E is added into the output graph.

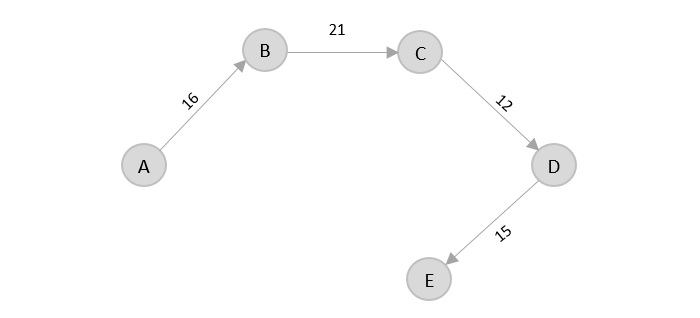
There’s only one edge from e, that is E → F. Therefore, it is added into the output graph.

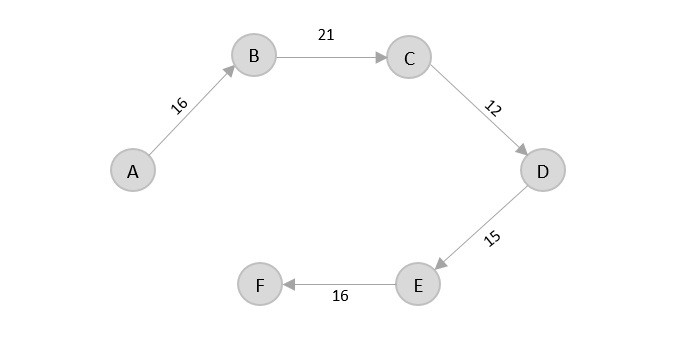
Again, even though F → C has lower distance than F → A, F → A is added into the output graph in order to avoid the cycle that would form and C is already visited once.

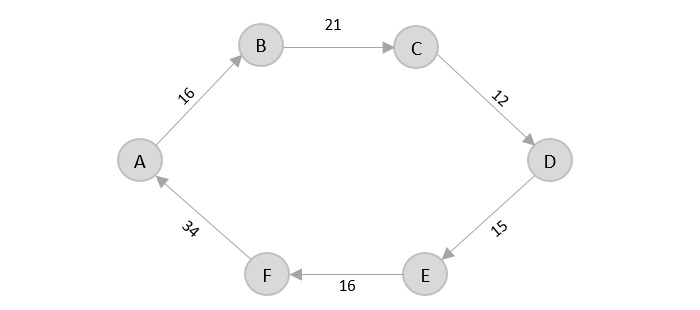
The shortest path that originates and ends at A is A → B → C → D → E → F → A

The cost of the path is: 16 + 21 + 12 + 15 + 16 + 34 = 114.

Even though, the cost of path could be decreased if it originates from other nodes but the question is not raised with respect to that.

The complete implementation of Travelling Salesman Problem using Greedy Approach is given below −

The Federal Register

The daily journal of the united states government, request access.

Due to aggressive automated scraping of FederalRegister.gov and eCFR.gov, programmatic access to these sites is limited to access to our extensive developer APIs.

If you are human user receiving this message, we can add your IP address to a set of IPs that can access FederalRegister.gov & eCFR.gov; complete the CAPTCHA (bot test) below and click "Request Access". This process will be necessary for each IP address you wish to access the site from, requests are valid for approximately one quarter (three months) after which the process may need to be repeated.

An official website of the United States government.

If you want to request a wider IP range, first request access for your current IP, and then use the "Site Feedback" button found in the lower left-hand side to make the request.