travelling salesman algorithm steps

• Data Structures
• Linked List
• Binary Tree
• Binary Search Tree
• Segment Tree
• Disjoint Set Union
• Fenwick Tree
• Red-Black Tree
• Advanced Data Structures
• Graph Data Structure And Algorithms
• Introduction to Graphs - Data Structure and Algorithm Tutorials
• Graph and its representations
• Types of Graphs with Examples
• Basic Properties of a Graph
• Applications, Advantages and Disadvantages of Graph
• Transpose graph
• Difference Between Graph and Tree

BFS and DFS on Graph

• Breadth First Search or BFS for a Graph
• Depth First Search or DFS for a Graph
• Applications, Advantages and Disadvantages of Depth First Search (DFS)
• Applications, Advantages and Disadvantages of Breadth First Search (BFS)
• Iterative Depth First Traversal of Graph
• BFS for Disconnected Graph
• Transitive Closure of a Graph using DFS
• Difference between BFS and DFS

Cycle in a Graph

• Detect Cycle in a Directed Graph
• Detect cycle in an undirected graph
• Detect Cycle in a directed graph using colors
• Detect a negative cycle in a Graph | (Bellman Ford)
• Cycles of length n in an undirected and connected graph
• Detecting negative cycle using Floyd Warshall
• Clone a Directed Acyclic Graph

Shortest Paths in Graph

• How to find Shortest Paths from Source to all Vertices using Dijkstra's Algorithm
• Bellman–Ford Algorithm
• Floyd Warshall Algorithm
• Johnson's algorithm for All-pairs shortest paths
• Shortest Path in Directed Acyclic Graph
• Multistage Graph (Shortest Path)
• Shortest path in an unweighted graph
• Karp's minimum mean (or average) weight cycle algorithm
• 0-1 BFS (Shortest Path in a Binary Weight Graph)
• Find minimum weight cycle in an undirected graph

Minimum Spanning Tree in Graph

• Kruskal’s Minimum Spanning Tree (MST) Algorithm
• Difference between Prim's and Kruskal's algorithm for MST
• Applications of Minimum Spanning Tree
• Total number of Spanning Trees in a Graph
• Minimum Product Spanning Tree
• Reverse Delete Algorithm for Minimum Spanning Tree

Topological Sorting in Graph

• Topological Sorting
• All Topological Sorts of a Directed Acyclic Graph
• Kahn's algorithm for Topological Sorting
• Maximum edges that can be added to DAG so that it remains DAG
• Longest Path in a Directed Acyclic Graph
• Topological Sort of a graph using departure time of vertex

Connectivity of Graph

• Articulation Points (or Cut Vertices) in a Graph
• Biconnected Components
• Bridges in a graph
• Eulerian path and circuit for undirected graph
• Fleury's Algorithm for printing Eulerian Path or Circuit
• Strongly Connected Components
• Count all possible walks from a source to a destination with exactly k edges
• Euler Circuit in a Directed Graph
• Word Ladder (Length of shortest chain to reach a target word)
• Find if an array of strings can be chained to form a circle | Set 1
• Tarjan's Algorithm to find Strongly Connected Components
• Paths to travel each nodes using each edge (Seven Bridges of Königsberg)
• Dynamic Connectivity | Set 1 (Incremental)

Maximum flow in a Graph

• Max Flow Problem Introduction
• Ford-Fulkerson Algorithm for Maximum Flow Problem
• Find maximum number of edge disjoint paths between two vertices
• Find minimum s-t cut in a flow network
• Maximum Bipartite Matching
• Channel Assignment Problem
• Introduction to Push Relabel Algorithm
• Introduction and implementation of Karger's algorithm for Minimum Cut
• Dinic's algorithm for Maximum Flow

Some must do problems on Graph

• Find size of the largest region in Boolean Matrix
• Count number of trees in a forest
• A Peterson Graph Problem
• Clone an Undirected Graph
• Introduction to Graph Coloring

Traveling Salesman Problem (TSP) Implementation

• Introduction and Approximate Solution for Vertex Cover Problem
• Erdos Renyl Model (for generating Random Graphs)
• Chinese Postman or Route Inspection | Set 1 (introduction)
• Hierholzer's Algorithm for directed graph
• Boggle (Find all possible words in a board of characters) | Set 1
• Hopcroft–Karp Algorithm for Maximum Matching | Set 1 (Introduction)
• Construct a graph from given degrees of all vertices
• Determine whether a universal sink exists in a directed graph
• Number of sink nodes in a graph
• Two Clique Problem (Check if Graph can be divided in two Cliques)

Travelling Salesman Problem (TSP) : Given a set of cities and distances between every pair of cities, the problem is to find the shortest possible route that visits every city exactly once and returns to the starting point.  Note the difference between Hamiltonian Cycle and TSP. The Hamiltonian cycle problem is to find if there exists a tour that visits every city exactly once. Here we know that Hamiltonian Tour exists (because the graph is complete) and in fact, many such tours exist, the problem is to find a minimum weight Hamiltonian Cycle.  For example, consider the graph shown in the figure on the right side. A TSP tour in the graph is 1-2-4-3-1. The cost of the tour is 10+25+30+15 which is 80. The problem is a famous NP-hard problem. There is no polynomial-time known solution for this problem.   

Examples: 

In this post, the implementation of a simple solution is discussed.

• Consider city 1 as the starting and ending point. Since the route is cyclic, we can consider any point as a starting point.
• Generate all (n-1)! permutations of cities.
• Calculate the cost of every permutation and keep track of the minimum cost permutation.
• Return the permutation with minimum cost.

Below is the implementation of the above idea 

Time complexity:  O(n!) where n is the number of vertices in the graph. This is because the algorithm uses the next_permutation function which generates all the possible permutations of the vertex set.  Auxiliary Space: O(n) as we are using a vector to store all the vertices.

Please Login to comment...

Similar reads.

• NP Complete

Improve your Coding Skills with Practice

What kind of Experience do you want to share?

• Data Structures & Algorithms
• DSA - Overview
• DSA - Environment Setup
• DSA - Algorithms Basics
• DSA - Asymptotic Analysis
• Data Structures
• DSA - Data Structure Basics
• DSA - Data Structures and Types
• DSA - Array Data Structure
• Linked Lists
• DSA - Linked List Data Structure
• DSA - Doubly Linked List Data Structure
• DSA - Circular Linked List Data Structure
• Stack & Queue
• DSA - Stack Data Structure
• DSA - Expression Parsing
• DSA - Queue Data Structure
• Searching Algorithms
• DSA - Searching Algorithms
• DSA - Linear Search Algorithm
• DSA - Binary Search Algorithm
• DSA - Interpolation Search
• DSA - Jump Search Algorithm
• DSA - Exponential Search
• DSA - Fibonacci Search
• DSA - Sublist Search
• DSA - Hash Table
• Sorting Algorithms
• DSA - Sorting Algorithms
• DSA - Bubble Sort Algorithm
• DSA - Insertion Sort Algorithm
• DSA - Selection Sort Algorithm
• DSA - Merge Sort Algorithm
• DSA - Shell Sort Algorithm
• DSA - Heap Sort
• DSA - Bucket Sort Algorithm
• DSA - Counting Sort Algorithm
• DSA - Radix Sort Algorithm
• DSA - Quick Sort Algorithm
• Graph Data Structure
• DSA - Graph Data Structure
• DSA - Depth First Traversal
• DSA - Breadth First Traversal
• DSA - Spanning Tree
• Tree Data Structure
• DSA - Tree Data Structure
• DSA - Tree Traversal
• DSA - Binary Search Tree
• DSA - AVL Tree
• DSA - Red Black Trees
• DSA - B Trees
• DSA - B+ Trees
• DSA - Splay Trees
• DSA - Tries
• DSA - Heap Data Structure
• DSA - Recursion Algorithms
• DSA - Tower of Hanoi Using Recursion
• DSA - Fibonacci Series Using Recursion
• Divide and Conquer
• DSA - Divide and Conquer
• DSA - Max-Min Problem
• DSA - Strassen's Matrix Multiplication
• DSA - Karatsuba Algorithm
• Greedy Algorithms
• DSA - Greedy Algorithms
• DSA - Travelling Salesman Problem (Greedy Approach)
• DSA - Prim's Minimal Spanning Tree
• DSA - Kruskal's Minimal Spanning Tree
• DSA - Dijkstra's Shortest Path Algorithm
• DSA - Map Colouring Algorithm
• DSA - Fractional Knapsack Problem
• DSA - Job Sequencing with Deadline
• DSA - Optimal Merge Pattern Algorithm
• Dynamic Programming
• DSA - Dynamic Programming
• DSA - Matrix Chain Multiplication
• DSA - Floyd Warshall Algorithm
• DSA - 0-1 Knapsack Problem
• DSA - Longest Common Subsequence Algorithm
• DSA - Travelling Salesman Problem (Dynamic Approach)
• Approximation Algorithms
• DSA - Approximation Algorithms
• DSA - Vertex Cover Algorithm
• DSA - Set Cover Problem
• DSA - Travelling Salesman Problem (Approximation Approach)
• Randomized Algorithms
• DSA - Randomized Algorithms
• DSA - Randomized Quick Sort Algorithm
• DSA - Karger’s Minimum Cut Algorithm
• DSA - Fisher-Yates Shuffle Algorithm
• DSA Useful Resources
• DSA - Questions and Answers
• DSA - Quick Guide
• DSA - Useful Resources
• DSA - Discussion
• Selected Reading
• UPSC IAS Exams Notes
• Developer's Best Practices
• Questions and Answers
• Effective Resume Writing
• HR Interview Questions
• Computer Glossary

Travelling Salesman Problem (Greedy Approach)

Travelling salesperson algorithm.

The travelling salesman problem is a graph computational problem where the salesman needs to visit all cities (represented using nodes in a graph) in a list just once and the distances (represented using edges in the graph) between all these cities are known. The solution that is needed to be found for this problem is the shortest possible route in which the salesman visits all the cities and returns to the origin city.

If you look at the graph below, considering that the salesman starts from the vertex ‘a’, they need to travel through all the remaining vertices b, c, d, e, f and get back to ‘a’ while making sure that the cost taken is minimum.

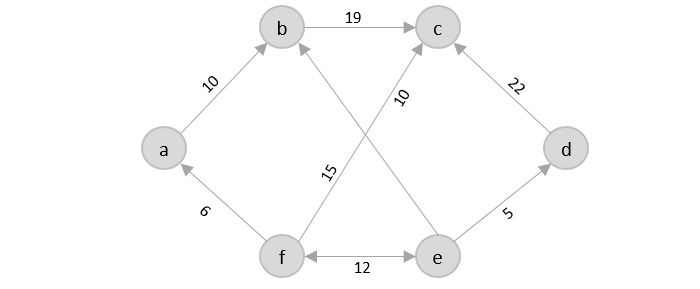
There are various approaches to find the solution to the travelling salesman problem: naive approach, greedy approach, dynamic programming approach, etc. In this tutorial we will be learning about solving travelling salesman problem using greedy approach.

As the definition for greedy approach states, we need to find the best optimal solution locally to figure out the global optimal solution. The inputs taken by the algorithm are the graph G {V, E}, where V is the set of vertices and E is the set of edges. The shortest path of graph G starting from one vertex returning to the same vertex is obtained as the output.

Travelling salesman problem takes a graph G {V, E} as an input and declare another graph as the output (say G’) which will record the path the salesman is going to take from one node to another.

The algorithm begins by sorting all the edges in the input graph G from the least distance to the largest distance.

The first edge selected is the edge with least distance, and one of the two vertices (say A and B) being the origin node (say A).

Then among the adjacent edges of the node other than the origin node (B), find the least cost edge and add it onto the output graph.

Continue the process with further nodes making sure there are no cycles in the output graph and the path reaches back to the origin node A.

However, if the origin is mentioned in the given problem, then the solution must always start from that node only. Let us look at some example problems to understand this better.

Consider the following graph with six cities and the distances between them −

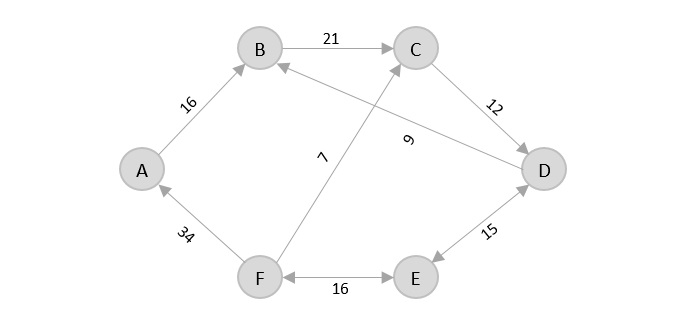
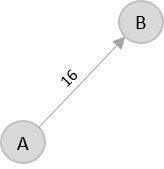
From the given graph, since the origin is already mentioned, the solution must always start from that node. Among the edges leading from A, A → B has the shortest distance.

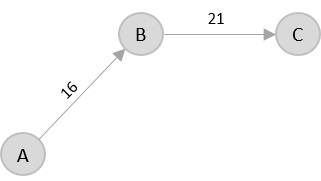
Then, B → C has the shortest and only edge between, therefore it is included in the output graph.

There’s only one edge between C → D, therefore it is added to the output graph.

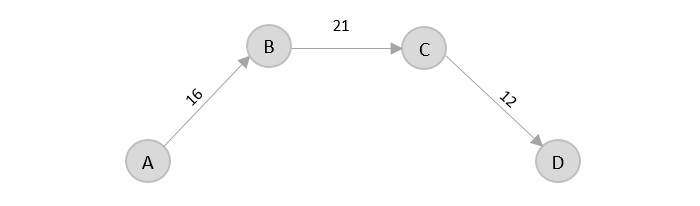
There’s two outward edges from D. Even though, D → B has lower distance than D → E, B is already visited once and it would form a cycle if added to the output graph. Therefore, D → E is added into the output graph.

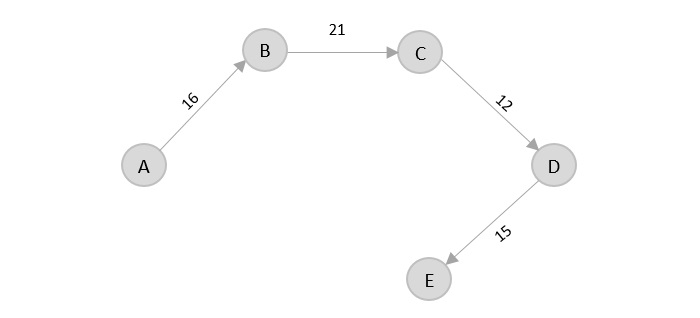
There’s only one edge from e, that is E → F. Therefore, it is added into the output graph.

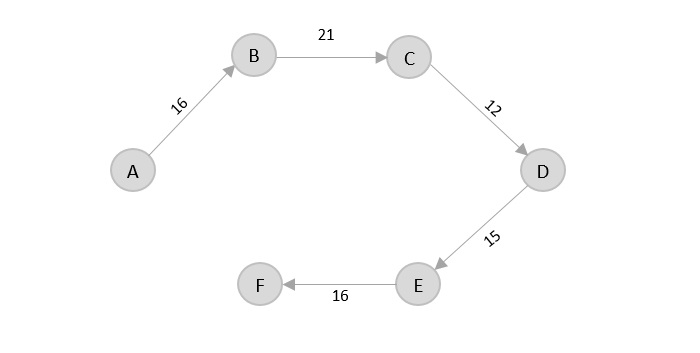
Again, even though F → C has lower distance than F → A, F → A is added into the output graph in order to avoid the cycle that would form and C is already visited once.

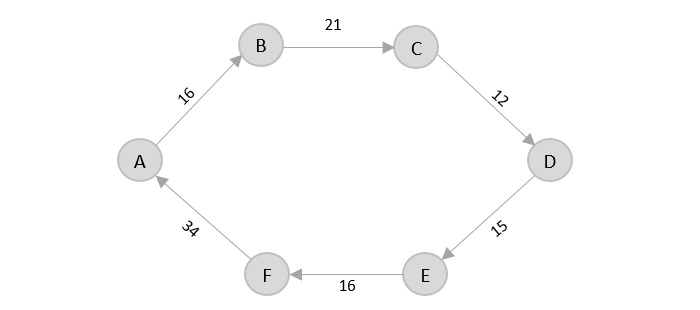
The shortest path that originates and ends at A is A → B → C → D → E → F → A

The cost of the path is: 16 + 21 + 12 + 15 + 16 + 34 = 114.

Even though, the cost of path could be decreased if it originates from other nodes but the question is not raised with respect to that.

The complete implementation of Travelling Salesman Problem using Greedy Approach is given below −

To Continue Learning Please Login

Travelling Salesman Problem: Python, C++ Algorithm

What is the Travelling Salesman Problem (TSP)?

Travelling Salesman Problem (TSP) is a classic combinatorics problem of theoretical computer science. The problem asks to find the shortest path in a graph with the condition of visiting all the nodes only one time and returning to the origin city.

The problem statement gives a list of cities along with the distances between each city.

Objective: To start from the origin city, visit other cities only once, and return to the original city again. Our target is to find the shortest possible path to complete the round-trip route.

Example of TSP

Here a graph is given where 1, 2, 3, and 4 represent the cities, and the weight associated with every edge represents the distance between those cities.

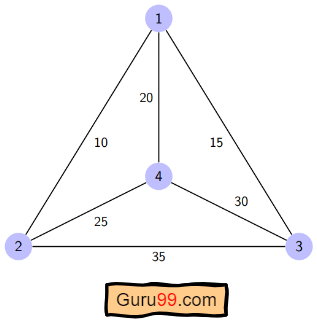
The goal is to find the shortest possible path for the tour that starts from the origin city, traverses the graph while only visiting the other cities or nodes once, and returns to the origin city.

For the above graph, the optimal route is to follow the minimum cost path: 1-2-4-3-1. And this shortest route would cost 10+25+30+15 =80

Different Solutions to Travelling Salesman Problem

Travelling Salesman Problem (TSP) is classified as a NP-hard problem due to having no polynomial time algorithm. The complexity increases exponentially by increasing the number of cities.

There are multiple ways to solve the traveling salesman problem (tsp). Some popular solutions are:

The brute force approach is the naive method for solving traveling salesman problems. In this approach, we first calculate all possible paths and then compare them. The number of paths in a graph consisting of n cities is n! It is computationally very expensive to solve the traveling salesman problem in this brute force approach.

The branch-and-bound method: The problem is broken down into sub-problems in this approach. The solution of those individual sub-problems would provide an optimal solution.

This tutorial will demonstrate a dynamic programming approach, the recursive version of this branch-and-bound method, to solve the traveling salesman problem.

Dynamic programming is such a method for seeking optimal solutions by analyzing all possible routes. It is one of the exact solution methods that solve traveling salesman problems through relatively higher cost than the greedy methods that provide a near-optimal solution.

The computational complexity of this approach is O(N^2 * 2^N) which is discussed later in this article.

The nearest neighbor method is a heuristic-based greedy approach where we choose the nearest neighbor node. This approach is computationally less expensive than the dynamic approach. But it does not provide the guarantee of an optimal solution. This method is used for near-optimal solutions.

Algorithm for Traveling Salesman Problem

We will use the dynamic programming approach to solve the Travelling Salesman Problem (TSP).

Before starting the algorithm, let’s get acquainted with some terminologies:

• A graph G=(V, E), which is a set of vertices and edges.
• V is the set of vertices.
• E is the set of edges.
• Vertices are connected through edges.
• Dist(i,j) denotes the non-negative distance between two vertices, i and j.

Let’s assume S is the subset of cities and belongs to {1, 2, 3, …, n} where 1, 2, 3…n are the cities and i, j are two cities in that subset. Now cost(i, S, j) is defined in such a way as the length of the shortest path visiting node in S, which is exactly once having the starting and ending point as i and j respectively.

For example, cost (1, {2, 3, 4}, 1) denotes the length of the shortest path where:

• Starting city is 1
• Cities 2, 3, and 4 are visited only once
• The ending point is 1

The dynamic programming algorithm would be:

• Set cost(i, , i) = 0, which means we start and end at i, and the cost is 0.
• When |S| > 1, we define cost(i, S, 1) = ∝ where i !=1 . Because initially, we do not know the exact cost to reach city i to city 1 through other cities.
• Now, we need to start at 1 and complete the tour. We need to select the next city in such a way-

cost(i, S, j)=min cost (i, S−{i}, j)+dist(i,j) where i∈S and i≠j

For the given figure, the adjacency matrix would be the following:

Let’s see how our algorithm works:

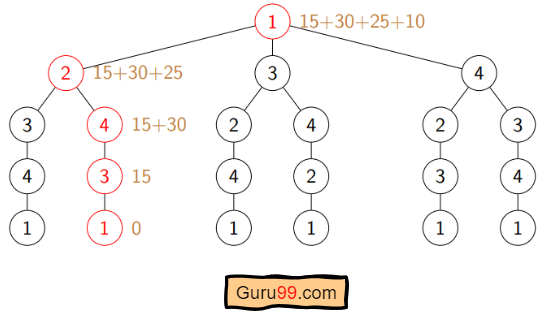
Step 1) We are considering our journey starting at city 1, visit other cities once and return to city 1.

Step 2) S is the subset of cities. According to our algorithm, for all |S| > 1, we will set the distance cost(i, S, 1) = ∝. Here cost(i, S, j) means we are starting at city i, visiting the cities of S once, and now we are at city j. We set this path cost as infinity because we do not know the distance yet. So the values will be the following:

Cost (2, {3, 4}, 1) = ∝ ; the notation denotes we are starting at city 2, going through cities 3, 4, and reaching 1. And the path cost is infinity. Similarly-

cost(3, {2, 4}, 1) = ∝

cost(4, {2, 3}, 1) = ∝

Step 3) Now, for all subsets of S, we need to find the following:

cost(i, S, j)=min cost (i, S−{i}, j)+dist(i,j), where j∈S and i≠j

That means the minimum cost path for starting at i, going through the subset of cities once, and returning to city j. Considering that the journey starts at city 1, the optimal path cost would be= cost(1, {other cities}, 1).

Let’s find out how we could achieve that:

Now S = {1, 2, 3, 4}. There are four elements. Hence the number of subsets will be 2^4 or 16. Those subsets are-

1) |S| = Null:

2) |S| = 1:

{{1}, {2}, {3}, {4}}

3) |S| = 2:

{{1, 2}, {1, 3}, {1, 4}, {2, 3}, {2, 4}, {3, 4}}

4) |S| = 3:

{{1, 2, 3}, {1, 2, 4}, {2, 3, 4}, {1, 3, 4}}

5) |S| = 4:

{{1, 2, 3, 4}}

As we are starting at 1, we could discard the subsets containing city 1.

The algorithm calculation:

1) |S| = Φ:

cost (2, Φ, 1) = dist(2, 1) = 10

cost (3, Φ, 1) = dist(3, 1) = 15

cost (4, Φ, 1) = dist(4, 1) = 20

cost (2, {3}, 1) = dist(2, 3) + cost (3, Φ, 1) = 35+15 = 50

cost (2, {4}, 1) = dist(2, 4) + cost (4, Φ, 1) = 25+20 = 45

cost (3, {2}, 1) = dist(3, 2) + cost (2, Φ, 1) = 35+10 = 45

cost (3, {4}, 1) = dist(3, 4) + cost (4, Φ, 1) = 30+20 = 50

cost (4, {2}, 1) = dist(4, 2) + cost (2, Φ, 1) = 25+10 = 35

cost (4, {3}, 1) = dist(4, 3) + cost (3, Φ, 1) = 30+15 = 45

cost (2, {3, 4}, 1) = min [ dist[2,3]+Cost(3,{4},1) = 35+50 = 85,

dist[2,4]+Cost(4,{3},1) = 25+45 = 70 ] = 70

cost (3, {2, 4}, 1) = min [ dist[3,2]+Cost(2,{4},1) = 35+45 = 80,

dist[3,4]+Cost(4,{2},1) = 30+35 = 65 ] = 65

cost (4, {2, 3}, 1) = min [ dist[4,2]+Cost(2,{3},1) = 25+50 = 75

dist[4,3]+Cost(3,{2},1) = 30+45 = 75 ] = 75

cost (1, {2, 3, 4}, 1) = min [ dist[1,2]+Cost(2,{3,4},1) = 10+70 = 80

dist[1,3]+Cost(3,{2,4},1) = 15+65 = 80

dist[1,4]+Cost(4,{2,3},1) = 20+75 = 95 ] = 80

So the optimal solution would be 1-2-4-3-1

Pseudo-code

Implementation in c/c++.

Here’s the implementation in C++ :

Implementation in Python

Academic solutions to tsp.

Computer scientists have spent years searching for an improved polynomial time algorithm for the Travelling Salesman Problem. Until now, the problem is still NP-hard.

Though some of the following solutions were published in recent years that have reduced the complexity to a certain degree:

• The classical symmetric TSP is solved by the Zero Suffix Method.
• The Biogeography‐based Optimization Algorithm is based on the migration strategy to solve the optimization problems that can be planned as TSP.
• Multi-Objective Evolutionary Algorithm is designed for solving multiple TSP based on NSGA-II.
• The Multi-Agent System solves the TSP of N cities with fixed resources.

Application of Traveling Salesman Problem

Travelling Salesman Problem (TSP) is applied in the real world in both its purest and modified forms. Some of those are:

• Planning, logistics, and manufacturing microchips : Chip insertion problems naturally arise in the microchip industry. Those problems can be planned as traveling salesman problems.
• DNA sequencing : Slight modification of the traveling salesman problem can be used in DNA sequencing. Here, the cities represent the DNA fragments, and the distance represents the similarity measure between two DNA fragments.
• Astronomy : The Travelling Salesman Problem is applied by astronomers to minimize the time spent observing various sources.
• Optimal control problem : Travelling Salesman Problem formulation can be applied in optimal control problems. There might be several other constraints added.

Complexity Analysis of TSP

So the total time complexity for an optimal solution would be the Number of nodes * Number of subproblems * time to solve each sub-problem. The time complexity can be defined as O(N 2 * 2^N).

• Space Complexity: The dynamic programming approach uses memory to store C(S, i), where S is a subset of the vertices set. There is a total of 2 N subsets for each node. So, the space complexity is O(2^N).

Next, you’ll learn about Sieve of Eratosthenes Algorithm

• Linear Search: Python, C++ Example
• DAA Tutorial PDF: Design and Analysis of Algorithms
• Heap Sort Algorithm (With Code in Python and C++)
• Kadence’s Algorithm: Largest Sum Contiguous Subarray
• Radix Sort Algorithm in Data Structure
• Doubly Linked List: C++, Python (Code Example)
• Singly Linked List in Data Structures
• Adjacency List and Matrix Representation of Graph

• Google OR-Tools
• Español – América Latina
• Português – Brasil
• Tiếng Việt

Traveling Salesperson Problem

This section presents an example that shows how to solve the Traveling Salesperson Problem (TSP) for the locations shown on the map below.

The following sections present programs in Python, C++, Java, and C# that solve the TSP using OR-Tools

Create the data

The code below creates the data for the problem.

The distance matrix is an array whose i , j entry is the distance from location i to location j in miles, where the array indices correspond to the locations in the following order:

The data also includes:

• The number of vehicles in the problem, which is 1 because this is a TSP. (For a vehicle routing problem (VRP), the number of vehicles can be greater than 1.)
• The depot : the start and end location for the route. In this case, the depot is 0, which corresponds to New York.

Other ways to create the distance matrix

In this example, the distance matrix is explicitly defined in the program. It's also possible to use a function to calculate distances between locations: for example, the Euclidean formula for the distance between points in the plane. However, it's still more efficient to pre-compute all the distances between locations and store them in a matrix, rather than compute them at run time. See Example: drilling a circuit board for an example that creates the distance matrix this way.

Another alternative is to use the Google Maps Distance Matrix API to dynamically create a distance (or travel time) matrix for a routing problem.

Create the routing model

The following code in the main section of the programs creates the index manager ( manager ) and the routing model ( routing ). The method manager.IndexToNode converts the solver's internal indices (which you can safely ignore) to the numbers for locations. Location numbers correspond to the indices for the distance matrix.

The inputs to RoutingIndexManager are:

• The number of rows of the distance matrix, which is the number of locations (including the depot).
• The number of vehicles in the problem.
• The node corresponding to the depot.

Create the distance callback

To use the routing solver, you need to create a distance (or transit) callback : a function that takes any pair of locations and returns the distance between them. The easiest way to do this is using the distance matrix.

The following function creates the callback and registers it with the solver as transit_callback_index .

The callback accepts two indices, from_index and to_index , and returns the corresponding entry of the distance matrix.

Set the cost of travel

The arc cost evaluator tells the solver how to calculate the cost of travel between any two locations — in other words, the cost of the edge (or arc) joining them in the graph for the problem. The following code sets the arc cost evaluator.

In this example, the arc cost evaluator is the transit_callback_index , which is the solver's internal reference to the distance callback. This means that the cost of travel between any two locations is just the distance between them. However, in general the costs can involve other factors as well.

You can also define multiple arc cost evaluators that depend on which vehicle is traveling between locations, using the method routing.SetArcCostEvaluatorOfVehicle() . For example, if the vehicles have different speeds, you could define the cost of travel between locations to be the distance divided by the vehicle's speed — in other words, the travel time.

Set search parameters

The following code sets the default search parameters and a heuristic method for finding the first solution:

The code sets the first solution strategy to PATH_CHEAPEST_ARC , which creates an initial route for the solver by repeatedly adding edges with the least weight that don't lead to a previously visited node (other than the depot). For other options, see First solution strategy .

Add the solution printer

The function that displays the solution returned by the solver is shown below. The function extracts the route from the solution and prints it to the console.

The function displays the optimal route and its distance, which is given by ObjectiveValue() .

Solve and print the solution

Finally, you can call the solver and print the solution:

This returns the solution and displays the optimal route.

Run the programs

When you run the programs, they display the following output.

In this example, there's only one route because it's a TSP. But in more general vehicle routing problems, the solution contains multiple routes.

Save routes to a list or array

As an alternative to printing the solution directly, you can save the route (or routes, for a VRP) to a list or array. This has the advantage of making the routes available in case you want to do something with them later. For example, you could run the program several times with different parameters and save the routes in the returned solutions to a file for comparison.

The following functions save the routes in the solution to any VRP (possibly with multiple vehicles) as a list (Python) or an array (C++).

You can use these functions to get the routes in any of the VRP examples in the Routing section.

The following code displays the routes.

For the current example, this code returns the following route:

As an exercise, modify the code above to format the output the same way as the solution printer for the program.

Complete programs

The complete TSP programs are shown below.

Example: drilling a circuit board

The next example involves drilling holes in a circuit board with an automated drill. The problem is to find the shortest route for the drill to take on the board in order to drill all of the required holes. The example is taken from TSPLIB, a library of TSP problems.

Here's scatter chart of the locations for the holes:

The following sections present programs that find a good solution to the circuit board problem, using the solver's default search parameters. After that, we'll show how to find a better solution by changing the search strategy .

The data for the problem consist of 280 points in the plane, shown in the scatter chart above. The program creates the data in an array of ordered pairs corresponding to the points in the plane, as shown below.

Compute the distance matrix

The function below computes the Euclidean distance between any two points in the data and stores it in an array. Because the routing solver works over the integers, the function rounds the computed distances to integers. Rounding doesn't affect the solution in this example, but might in other cases. See Scaling the distance matrix for a way to avoid possible rounding issues.

Add the distance callback

The code that creates the distance callback is almost the same as in the previous example. However, in this case the program calls the function that computes the distance matrix before adding the callback.

Solution printer

The following function prints the solution to the console. To keep the output more compact, the function displays just the indices of the locations in the route.

Main function

The main function is essentially the same as the one in the previous example , but also includes a call to the function that creates the distance matrix.

Running the program

The complete programs are shown in the next section . When you run the program, it displays the following route:

Here's a graph of the corresponding route:

The OR-Tools library finds the above tour very quickly: in less than a second on a typical computer. The total length of the above tour is 2790.

Here are the complete programs for the circuit board example.

Changing the search strategy

The routing solver does not always return the optimal solution to a TSP, because routing problems are computationally intractable. For instance, the solution returned in the previous example is not the optimal route.

To find a better solution, you can use a more advanced search strategy, called guided local search , which enables the solver to escape a local minimum — a solution that is shorter than all nearby routes, but which is not the global minimum. After moving away from the local minimum, the solver continues the search.

The examples below show how to set a guided local search for the circuit board example.

For other local search strategies, see Local search options .

The examples above also enable logging for the search. While logging isn't required, it can be useful for debugging.

When you run the program after making the changes shown above, you get the following solution, which is shorter than the solution shown in the previous section .

For more search options, see Routing Options .

The best algorithms can now routinely solve TSP instances with tens of thousands of nodes. (The record at the time of writing is the pla85900 instance in TSPLIB, a VLSI application with 85,900 nodes. For certain instances with millions of nodes, solutions have been found guaranteed to be within 1% of an optimal tour.)

Scaling the distance matrix

Since the routing solver works over the integers, if your distance matrix has non-integer entries, you have to round the distances to integers. If some distances are small, rounding can affect the solution.

To avoid any issue with rounding, you can scale the distance matrix: multiply all entries of the matrix by a large number — say 100. This multiplies the length of any route by a factor of 100, but it doesn't change the solution. The advantage is that now when you round the matrix entries, the rounding amount (which is at most 0.5), is very small compared to the distances, so it won't affect the solution significantly.

If you scale the distance matrix, you also need to change the solution printer to divide the scaled route lengths by the scaling factor, so that it displays the unscaled distances of the routes.

Except as otherwise noted, the content of this page is licensed under the Creative Commons Attribution 4.0 License , and code samples are licensed under the Apache 2.0 License . For details, see the Google Developers Site Policies . Java is a registered trademark of Oracle and/or its affiliates.

Last updated 2023-01-16 UTC.

Reset password New user? Sign up

Existing user? Log in

Traveling Salesperson Problem

Already have an account? Log in here.

A salesperson needs to visit a set of cities to sell their goods. They know how many cities they need to go to and the distances between each city. In what order should the salesperson visit each city exactly once so that they minimize their travel time and so that they end their journey in their city of origin?

The traveling salesperson problem is an extremely old problem in computer science that is an extension of the Hamiltonian Circuit Problem . It has important implications in complexity theory and the P versus NP problem because it is an NP-Complete problem . This means that a solution to this problem cannot be found in polynomial time (it takes superpolynomial time to compute an answer). In other words, as the number of vertices increases linearly, the computation time to solve the problem increases exponentially.

The following image is a simple example of a network of cities connected by edges of a specific distance. The origin city is also marked.

Network of cities

Here is the solution for that network, it has a distance traveled of only 14. Any other path that the salesman can takes will result in a path length that is more than 14.

Relationship to Graphs

Special kinds of tsp, importance for p vs np, applications.

The traveling salesperson problem can be modeled as a graph . Specifically, it is typical a directed, weighted graph. Each city acts as a vertex and each path between cities is an edge. Instead of distances, each edge has a weight associated with it. In this model, the goal of the traveling salesperson problem can be defined as finding a path that visits every vertex, returns to the original vertex, and minimizes total weight.

To that end, many graph algorithms can be used on this model. Search algorithms like breadth-first search (BFS) , depth-first search (DFS) , and Dijkstra's shortest path algorithm can certainly be used, however, they do not take into consideration that fact that every vertex must be visited.

The Traveling Salesperson Problem (TSP), an NP-Complete problem, is notoriously complicated to solve. That is because the greedy approach is so computational intensive. The greedy approach to solving this problem would be to try every single possible path and see which one is the fastest. Try this conceptual question to see if you have a grasp for how hard it is to solve.

For a fully connected map with \(n\) cities, how many total paths are possible for the traveling salesperson? Show Answer There are (n-1)! total paths the salesperson can take. The computation needed to solve this problem in this way grows far too quickly to be a reasonable solution. If this map has only 5 cities, there are \(4!\), or 24, paths. However, if the size of this map is increased to 20 cities, there will be \(1.22 \cdot 10^{17}\) paths!

The greedy approach to TSP would go like this:

• Find all possible paths.
• Find the cost of every paths.
• Choose the path with the lowest cost.

Another version of a greedy approach might be: At every step in the algorithm, choose the best possible path. This version might go a little quicker, but it's not guaranteed to find the best answer, or an answer at all since it might hit a dead end.

For NP-Hard problems (a subset of NP-Complete problems) like TSP, exact solutions can only be implemented in a reasonable amount of time for small input sizes (maps with few cities). Otherwise, the best approach we can do is provide a heuristic to help the problem move forward in an optimal way. However, these approaches cannot be proven to be optimal because they always have some sort of downside.

Small input sizes

As described, in a previous section , the greedy approach to this problem has a complexity of \(O(n!)\). However, there are some approaches that decrease this computation time.

The Held-Karp Algorithm is one of the earliest applications of dynamic programming . Its complexity is much lower than the greedy approach at \(O(n^2 2^n)\). Basically what this algorithm says is that every sub path along an optimal path is itself an optimal path. So, computing an optimal path is the same as computing many smaller subpaths and adding them together.

Heuristics are a way of ranking possible next steps in an algorithm in the hopes of cutting down computation time for the entire algorithm. They are often a tradeoff of some attribute - such as completeness, accuracy, or precision - in favor of speed. Heuristics exist for the traveling salesperson problem as well.

The most simple heuristic for this problem is the greedy heuristic. This heuristic simply says, at each step of the network traversal, choose the best next step. In other words, always choose the closest city that you have not yet visited. This heuristic seems like a good one because it is simple and intuitive, and it is even used in practice sometimes, however there are heuristics that are proven to be more effective.

Christofides algorithm is another heuristic. It produces at most 1.5 times the optimal weight for TSP. This algorithm involves finding a minimum spanning tree for the network. Next, it creates matchings for the cities of an odd degree (meaning they have an odd number of edges coming out of them), calculates an eulerian path , and converts back to a TSP path.

Even though it is typically impossible to optimally solve TSP problems, there are cases of TSP problems that can be solved if certain conditions hold.

The metric-TSP is an instance of TSP that satisfies this condition: The distance from city A to city B is less than or equal to the distance from city A to city C plus the distance from city C to city B. Or,

\[distance_{AB} \leq distance_{AC} + distance_{CB}\]

This is a condition that holds in the real world, but it can't always be expected to hold for every TSP problem. But, with this inequality in place, the approximated path will be no more than twice the optimal path. Even better, we can bound the solution to a \(3/2\) approximation by using Christofide's Algorithm .

The euclidean-TSP has an even stricter constraint on the TSP input. It states that all cities' edges in the network must obey euclidean distances . Recent advances have shown that approximation algorithms using euclidean minimum spanning trees have reduced the runtime of euclidean-TSP, even though they are also NP-hard. In practice, though, simpler heuristics are still used.

The P versus NP problem is one of the leading questions in modern computer science. It asks whether or not every problem whose solution can be verified in polynomial time by a computer can also be solved in polynomial time by a computer. TSP, for example, cannot be solved in polynomial time (at least that's what is currently theorized). However, TSP can be solved in polynomial time when it is phrased like this: Given a graph and an integer, x, decide if there is a path of length x or less than x . It's easy to see that given a proposed answer to this question, it is simple to check if it is less than or equal to x.

The traveling salesperson problem, like other problems that are NP-Complete, are very important to this debate. That is because if a polynomial time solution can be found to this problems, then \(P = NP\). As it stands, most scientists believe that \(P \ne NP\).

The traveling salesperson problem has many applications. The obvious ones are in the transportation space. Planning delivery routes or flight patterns, for example, would benefit immensly from breakthroughs is this problem or in the P versus NP problem .

However, this same logic can be applied to many facets of planning as well. In robotics, for instance, planning the order in which to drill holes in a circuit board is a complex task due to the sheer number of holes that must be drawn.

The best and most important application of TSP, however, comes from the fact that it is an NP-Complete problem. That means that its practical applications amount to the applications of any problem that is NP-Complete. So, if there are significant breakthroughs for TSP, that means that those exact same breakthrough can be applied to any problem in the NP-Complete class.

Problem Loading...

Note Loading...

Set Loading...

Traveling Salesman Problem

Greedy algorithms for graphs: traveling salesman problem, introduction.

The Traveling Salesman Problem (TSP) is a classic optimization problem in graph theory. Given a set of cities and the distances between them, the task is to find the shortest possible route that allows a salesman to visit each city exactly once and return to the starting city. The TSP is known to be an NP-hard problem, meaning there is no known efficient algorithm to solve it optimally for large inputs. However, greedy algorithms offer a promising approach to finding approximate solutions.

Greedy Algorithms

A greedy algorithm is one that makes locally optimal choices at each step in hopes of finding a globally optimal solution. In the context of the TSP, a greedy algorithm constructs a tour by iteratively adding the nearest unvisited city to the current tour. Let's dive into the details and code examples to better understand how this works.

Algorithm Steps

The greedy algorithm for the TSP can be summarized in the following steps:

• Start with an empty tour and select an arbitrary starting city.
• Find the nearest unvisited city from the current city.
• Add this city to the tour.
• Mark the city as visited.
• Set the current city to the newly added city.
• Add the starting city back to the tour.
• The resulting tour is the approximate solution to the TSP.

Implementing the Algorithm

To illustrate the implementation of the greedy algorithm for the TSP, let's consider a small example using the following distance matrix:

| | City A | City B | City C | |-------|--------|--------|--------| | City A| 0 | 2 | 9 | | City B| 2 | 0 | 4 | | City C| 9 | 4 | 0 |

Example Run

Let's run our algorithm on the given distance matrix to find an approximate solution to the TSP:

The time complexity of the greedy algorithm for the TSP is O(n^2), where n is the number of cities. This is because, in each step, we iterate through all unvisited cities to find the nearest one. Despite being an approximate solution, the greedy algorithm often provides reasonable results and runs quickly for practical instances.

In this tutorial, we explored greedy algorithms for graphs, focusing specifically on the Traveling Salesman Problem. We learned the steps involved in the greedy algorithm for the TSP and implemented it in Python. By making locally optimal choices, the greedy algorithm offers an approach to finding approximate solutions for the TSP. While not always optimal, the greedy algorithm provides a good trade-off between efficiency and solution quality.

Hi, I'm Ada, your personal AI tutor. I can help you with any coding tutorial. Go ahead and ask me anything.

I have a question about this topic

Give more examples

DSA Tutorial

Linked lists, stacks & queues, hash tables, shortest path, minimum spanning tree, maximum flow, time complexity, dsa reference, dsa examples, dsa the traveling salesman problem.

The Traveling Salesman Problem

The Traveling Salesman Problem states that you are a salesperson and you must visit a number of cities or towns.

Rules : Visit every city only once, then return back to the city you started in.

Goal : Find the shortest possible route.

Except for the Held-Karp algorithm (which is quite advanced and time consuming, (\(O(2^n n^2)\)), and will not be described here), there is no other way to find the shortest route than to check all possible routes.

This means that the time complexity for solving this problem is \(O(n!)\), which means 720 routes needs to be checked for 6 cities, 40,320 routes must be checked for 8 cities, and if you have 10 cities to visit, more than 3.6 million routes must be checked!

Note: "!", or "factorial", is a mathematical operation used in combinatorics to find out how many possible ways something can be done. If there are 4 cities, each city is connected to every other city, and we must visit every city exactly once, there are \(4!= 4 \cdot 3 \cdot 2 \cdot 1 = 24\) different routes we can take to visit those cities.

The Traveling Salesman Problem (TSP) is a problem that is interesting to study because it is very practical, but so time consuming to solve, that it becomes nearly impossible to find the shortest route, even in a graph with just 20-30 vertices.

If we had an effective algorithm for solving The Traveling Salesman Problem, the consequences would be very big in many sectors, like for example chip design, vehicle routing, telecommunications, and urban planning.

Checking All Routes to Solve The Traveling Salesman Problem

To find the optimal solution to The Traveling Salesman Problem, we will check all possible routes, and every time we find a shorter route, we will store it, so that in the end we will have the shortest route.

Good: Finds the overall shortest route.

Bad: Requires an awful lot of calculation, especially for a large amount of cities, which means it is very time consuming.

How it works:

• Check the length of every possible route, one route at a time.
• Is the current route shorter than the shortest route found so far? If so, store the new shortest route.
• After checking all routes, the stored route is the shortest one.

Such a way of finding the solution to a problem is called brute force .

Brute force is not really an algorithm, it just means finding the solution by checking all possibilities, usually because of a lack of a better way to do it.

Speed: {{ inpVal }}

Finding the shortest route in The Traveling Salesman Problem by checking all routes (brute force).

Progress: {{progress}}%

n = {{vertices}} cities

{{vertices}}!={{posRoutes}} possible routes

Show every route: {{showCompares}}

The reason why the brute force approach of finding the shortest route (as shown above) is so time consuming is that we are checking all routes, and the number of possible routes increases really fast when the number of cities increases.

Finding the optimal solution to the Traveling Salesman Problem by checking all possible routes (brute force):

Using A Greedy Algorithm to Solve The Traveling Salesman Problem

Since checking every possible route to solve the Traveling Salesman Problem (like we did above) is so incredibly time consuming, we can instead find a short route by just going to the nearest unvisited city in each step, which is much faster.

Good: Finds a solution to the Traveling Salesman Problem much faster than by checking all routes.

Bad: Does not find the overall shortest route, it just finds a route that is much shorter than an average random route.

• Visit every city.
• The next city to visit is always the nearest of the unvisited cities from the city you are currently in.
• After visiting all cities, go back to the city you started in.

This way of finding an approximation to the shortest route in the Traveling Salesman Problem, by just going to the nearest unvisited city in each step, is called a greedy algorithm .

Finding an approximation to the shortest route in The Traveling Salesman Problem by always going to the nearest unvisited neighbor (greedy algorithm).

As you can see by running this simulation a few times, the routes that are found are not completely unreasonable. Except for a few times when the lines cross perhaps, especially towards the end of the algorithm, the resulting route is a lot shorter than we would get by choosing the next city at random.

Finding a near-optimal solution to the Traveling Salesman Problem using the nearest-neighbor algorithm (greedy):

Other Algorithms That Find Near-Optimal Solutions to The Traveling Salesman Problem

In addition to using a greedy algorithm to solve the Traveling Salesman Problem, there are also other algorithms that can find approximations to the shortest route.

These algorithms are popular because they are much more effective than to actually check all possible solutions, but as with the greedy algorithm above, they do not find the overall shortest route.

Algorithms used to find a near-optimal solution to the Traveling Salesman Problem include:

• 2-opt Heuristic: An algorithm that improves the solution step-by-step, in each step removing two edges and reconnecting the two paths in a different way to reduce the total path length.
• Genetic Algorithm: This is a type of algorithm inspired by the process of natural selection and use techniques such as selection, mutation, and crossover to evolve solutions to problems, including the TSP.
• Simulated Annealing: This method is inspired by the process of annealing in metallurgy. It involves heating and then slowly cooling a material to decrease defects. In the context of TSP, it's used to find a near-optimal solution by exploring the solution space in a way that allows for occasional moves to worse solutions, which helps to avoid getting stuck in local minima.
• Ant Colony Optimization: This algorithm is inspired by the behavior of ants in finding paths from the colony to food sources. It's a more complex probabilistic technique for solving computational problems which can be mapped to finding good paths through graphs.

Time Complexity for Solving The Traveling Salesman Problem

To get a near-optimal solution fast, we can use a greedy algorithm that just goes to the nearest unvisited city in each step, like in the second simulation on this page.

Solving The Traveling Salesman Problem in a greedy way like that, means that at each step, the distances from the current city to all other unvisited cities are compared, and that gives us a time complexity of \(O(n^2) \).

But finding the shortest route of them all requires a lot more operations, and the time complexity for that is \(O(n!)\), like mentioned earlier, which means that for 4 cities, there are 4! possible routes, which is the same as \(4 \cdot 3 \cdot 2 \cdot 1 = 24\). And for just 12 cities for example, there are \(12! = 12 \cdot 11 \cdot 10 \cdot \; ... \; \cdot 2 \cdot 1 = 479,001,600\) possible routes!

See the time complexity for the greedy algorithm \(O(n^2)\), versus the time complexity for finding the shortest route by comparing all routes \(O(n!)\), in the image below.

But there are two things we can do to reduce the number of routes we need to check.

In the Traveling Salesman Problem, the route starts and ends in the same place, which makes a cycle. This means that the length of the shortest route will be the same no matter which city we start in. That is why we have chosen a fixed city to start in for the simulation above, and that reduces the number of possible routes from \(n!\) to \((n-1)!\).

Also, because these routes go in cycles, a route has the same distance if we go in one direction or the other, so we actually just need to check the distance of half of the routes, because the other half will just be the same routes in the opposite direction, so the number of routes we need to check is actually \( \frac{(n-1)!}{2}\).

But even if we can reduce the number of routes we need to check to \( \frac{(n-1)!}{2}\), the time complexity is still \( O(n!)\), because for very big \(n\), reducing \(n\) by one and dividing by 2 does not make a significant change in how the time complexity grows when \(n\) is increased.

To better understand how time complexity works, go to this page .

Actual Traveling Salesman Problems Are More Complex

The edge weight in a graph in this context of The Traveling Salesman Problem tells us how hard it is to go from one point to another, and it is the total edge weight of a route we want to minimize.

So far on this page, the edge weight has been the distance in a straight line between two points. And that makes it much easier to explain the Traveling Salesman Problem, and to display it.

But in the real world there are many other things that affects the edge weight:

• Obstacles: When moving from one place to another, we normally try to avoid obstacles like trees, rivers, houses for example. This means it is longer and takes more time to go from A to B, and the edge weight value needs to be increased to factor that in, because it is not a straight line anymore.
• Transportation Networks: We usually follow a road or use public transport systems when traveling, and that also affects how hard it is to go (or send a package) from one place to another.
• Traffic Conditions: Travel congestion also affects the travel time, so that should also be reflected in the edge weight value.
• Legal and Political Boundaries: Crossing border for example, might make one route harder to choose than another, which means the shortest straight line route might be slower, or more costly.
• Economic Factors: Using fuel, using the time of employees, maintaining vehicles, all these things cost money and should also be factored into the edge weights.

As you can see, just using the straight line distances as the edge weights, might be too simple compared to the real problem. And solving the Traveling Salesman Problem for such a simplified problem model would probably give us a solution that is not optimal in a practical sense.

It is not easy to visualize a Traveling Salesman Problem when the edge length is not just the straight line distance between two points anymore, but the computer handles that very well.

COLOR PICKER

Contact Sales

If you want to use W3Schools services as an educational institution, team or enterprise, send us an e-mail: [email protected]

Report Error

If you want to report an error, or if you want to make a suggestion, send us an e-mail: [email protected]

Top Tutorials

Top references, top examples, get certified.

12.9 Traveling Salesperson Problem

Learning objectives.

After completing this section, you should be able to:

• Distinguish between brute force algorithms and greedy algorithms.
• List all distinct Hamilton cycles of a complete graph.
• Apply brute force method to solve traveling salesperson applications.
• Apply nearest neighbor method to solve traveling salesperson applications.

We looked at Hamilton cycles and paths in the previous sections Hamilton Cycles and Hamilton Paths . In this section, we will analyze Hamilton cycles in complete weighted graphs to find the shortest route to visit a number of locations and return to the starting point. Besides the many routing applications in which we need the shortest distance, there are also applications in which we search for the route that is least expensive or takes the least time. Here are a few less common applications that you can read about on a website set up by the mathematics department at the University of Waterloo in Ontario, Canada:

• Design of fiber optic networks
• Minimizing fuel expenses for repositioning satellites
• Development of semi-conductors for microchips
• A technique for mapping mammalian chromosomes in genome sequencing

Before we look at approaches to solving applications like these, let's discuss the two types of algorithms we will use.

Brute Force and Greedy Algorithms

An algorithm is a sequence of steps that can be used to solve a particular problem. We have solved many problems in this chapter, and the procedures that we used were different types of algorithms. In this section, we will use two common types of algorithms, a brute force algorithm and a greedy algorithm . A brute force algorithm begins by listing every possible solution and applying each one until the best solution is found. A greedy algorithm approaches a problem in stages, making the apparent best choice at each stage, then linking the choices together into an overall solution which may or may not be the best solution.

To understand the difference between these two algorithms, consider the tree diagram in Figure 12.187 . Suppose we want to find the path from left to right with the largest total sum. For example, branch A in the tree diagram has a sum of 10 + 2 + 11 + 13 = 36 10 + 2 + 11 + 13 = 36 .

To be certain that you pick the branch with greatest sum, you could list each sum from each of the different branches:

A : 10 + 2 + 11 + 13 = 36 10 + 2 + 11 + 13 = 36

B : 10 + 2 + 11 + 8 = 31 10 + 2 + 11 + 8 = 31

C : 10 + 2 + 15 + 1 = 28 10 + 2 + 15 + 1 = 28

D : 10 + 2 + 15 + 6 = 33 10 + 2 + 15 + 6 = 33

E : 10 + 7 + 3 + 20 = 40 10 + 7 + 3 + 20 = 40

F : 10 + 7 + 3 + 14 = 34 10 + 7 + 3 + 14 = 34

G : 10 + 7 + 4 + 11 = 32 10 + 7 + 4 + 11 = 32

H : 10 + 7 + 4 + 5 = 26 10 + 7 + 4 + 5 = 26

Then we know with certainty that branch E has the greatest sum.

Now suppose that you wanted to find the branch with the highest value, but you only were shown the tree diagram in phases, one step at a time.

After phase 1, you would have chosen the branch with 10 and 7. So far, you are following the same branch. Let’s look at the next phase.

After phase 2, based on the information you have, you will choose the branch with 10, 7 and 4. Now, you are following a different branch than before, but it is the best choice based on the information you have. Let’s look at the last phase.

After phase 3, you will choose branch G which has a sum of 32.

The process of adding the values on each branch and selecting the highest sum is an example of a brute force algorithm because all options were explored in detail. The process of choosing the branch in phases, based on the best choice at each phase is a greedy algorithm. Although a brute force algorithm gives us the ideal solution, it can take a very long time to implement. Imagine a tree diagram with thousands or even millions of branches. It might not be possible to check all the sums. A greedy algorithm, on the other hand, can be completed in a relatively short time, and generally leads to good solutions, but not necessarily the ideal solution.

Example 12.42

Distinguishing between brute force and greedy algorithms.

A cashier rings up a sale for $4.63 cents in U.S. currency. The customer pays with a $5 bill. The cashier would like to give the customer $0.37 in change using the fewest coins possible. The coins that can be used are quarters ($0.25), dimes ($0.10), nickels ($0.05), and pennies ($0.01). The cashier starts by selecting the coin of highest value less than or equal to $0.37, which is a quarter. This leaves $ 0.37 − $ 0.25 = $ 0.12 $ 0.37 − $ 0.25 = $ 0.12 . The cashier selects the coin of highest value less than or equal to $0.12, which is a dime. This leaves $ 0.12 − $ 0.10 = $ 0.02 $ 0.12 − $ 0.10 = $ 0.02 . The cashier selects the coin of highest value less than or equal to $0.02, which is a penny. This leaves $ 0.02 − $ 0.01 = $ 0.01 $ 0.02 − $ 0.01 = $ 0.01 . The cashier selects the coin of highest value less than or equal to $0.01, which is a penny. This leaves no remainder. The cashier used one quarter, one dime, and two pennies, which is four coins. Use this information to answer the following questions.

• Is the cashier’s approach an example of a greedy algorithm or a brute force algorithm? Explain how you know.
• The cashier’s solution is the best solution. In other words, four is the fewest number of coins possible. Is this consistent with the results of an algorithm of this kind? Explain your reasoning.
• The approach the cashier used is an example of a greedy algorithm, because the problem was approached in phases and the best choice was made at each phase. Also, it is not a brute force algorithm, because the cashier did not attempt to list out all possible combinations of coins to reach this conclusion.
• Yes, it is consistent. A greedy algorithm does not always yield the best result, but sometimes it does.

Your Turn 12.42

The traveling salesperson problem.

Now let’s focus our attention on the graph theory application known as the traveling salesperson problem (TSP) in which we must find the shortest route to visit a number of locations and return to the starting point.

Recall from Hamilton Cycles , the officer in the U.S. Air Force who is stationed at Vandenberg Air Force base and must drive to visit three other California Air Force bases before returning to Vandenberg. The officer needed to visit each base once. We looked at the weighted graph in Figure 12.192 representing the four U.S. Air Force bases: Vandenberg, Edwards, Los Angeles, and Beal and the distances between them.

Any route that visits each base and returns to the start would be a Hamilton cycle on the graph. If the officer wants to travel the shortest distance, this will correspond to a Hamilton cycle of lowest weight. We saw in Table 12.11 that there are six distinct Hamilton cycles (directed cycles) in a complete graph with four vertices, but some lie on the same cycle (undirected cycle) in the graph.

Since the distance between bases is the same in either direction, it does not matter if the officer travels clockwise or counterclockwise. So, there are really only three possible distances as shown in Figure 12.193 .

The possible distances are:

So, a Hamilton cycle of least weight is V → B → E → L → V (or the reverse direction). The officer should travel from Vandenberg to Beal to Edwards, to Los Angeles, and back to Vandenberg.

Finding Weights of All Hamilton Cycles in Complete Graphs

Notice that we listed all of the Hamilton cycles and found their weights when we solved the TSP about the officer from Vandenberg. This is a skill you will need to practice. To make sure you don't miss any, you can calculate the number of possible Hamilton cycles in a complete graph. It is also helpful to know that half of the directed cycles in a complete graph are the same cycle in reverse direction, so, you only have to calculate half the number of possible weights, and the rest are duplicates.

In a complete graph with n n vertices,

• The number of distinct Hamilton cycles is ( n − 1 ) ! ( n − 1 ) ! .
• There are at most ( n − 1 ) ! 2 ( n − 1 ) ! 2 different weights of Hamilton cycles.

TIP! When listing all the distinct Hamilton cycles in a complete graph, you can start them all at any vertex you choose. Remember, the cycle a → b → c → a is the same cycle as b → c → a → b so there is no need to list both.

Example 12.43

Calculating possible weights of hamilton cycles.

Suppose you have a complete weighted graph with vertices N, M, O , and P .

• Use the formula ( n − 1 ) ! ( n − 1 ) ! to calculate the number of distinct Hamilton cycles in the graph.
• Use the formula ( n − 1 ) ! 2 ( n − 1 ) ! 2 to calculate the greatest number of different weights possible for the Hamilton cycles.
• Are all of the distinct Hamilton cycles listed here? How do you know? Cycle 1: N → M → O → P → N Cycle 2: N → M → P → O → N Cycle 3: N → O → M → P → N Cycle 4: N → O → P → M → N Cycle 5: N → P → M → O → N Cycle 6: N → P → O → M → N
• Which pairs of cycles must have the same weights? How do you know?
• There are 4 vertices; so, n = 4 n = 4 . This means there are ( n − 1 ) ! = ( 4 − 1 ) ! = 3 ⋅ 2 ⋅ 1 = 6 ( n − 1 ) ! = ( 4 − 1 ) ! = 3 ⋅ 2 ⋅ 1 = 6 distinct Hamilton cycles beginning at any given vertex.
• Since n = 4 n = 4 , there are ( n − 1 ) ! 2 = ( 4 − 1 ) ! 2 = 6 2 = 3 ( n − 1 ) ! 2 = ( 4 − 1 ) ! 2 = 6 2 = 3 possible weights.
• Yes, they are all distinct cycles and there are 6 of them.
• Cycles 1 and 6 have the same weight, Cycles 2 and 4 have the same weight, and Cycles 3 and 5 have the same weight, because these pairs follow the same route through the graph but in reverse.

TIP! When listing the possible cycles, ignore the vertex where the cycle begins and ends and focus on the ways to arrange the letters that represent the vertices in the middle. Using a systematic approach is best; for example, if you must arrange the letters M, O, and P, first list all those arrangements beginning with M, then beginning with O, and then beginning with P, as we did in Example 12.42.

Your Turn 12.43

The brute force method.

The method we have been using to find a Hamilton cycle of least weight in a complete graph is a brute force algorithm, so it is called the brute force method . The steps in the brute force method are:

Step 1: Calculate the number of distinct Hamilton cycles and the number of possible weights.

Step 2: List all possible Hamilton cycles.

Step 3: Find the weight of each cycle.

Step 4: Identify the Hamilton cycle of lowest weight.

Example 12.44

Applying the brute force method.

On the next assignment, the air force officer must leave from Travis Air Force base, visit Beal, Edwards, and Vandenberg Air Force bases each exactly once and return to Travis Air Force base. There is no need to visit Los Angeles Air Force base. Use Figure 12.194 to find the shortest route.

Step 1: Since there are 4 vertices, there will be ( 4 − 1 ) ! = 3 ! = 6 ( 4 − 1 ) ! = 3 ! = 6 cycles, but half of them will be the reverse of the others; so, there will be ( 4 − 1 ) ! 2 = 6 2 = 3 ( 4 − 1 ) ! 2 = 6 2 = 3 possible distances.

Step 2: List all the Hamilton cycles in the subgraph of the graph in Figure 12.195 .

To find the 6 cycles, focus on the three vertices in the middle, B, E, and V . The arrangements of these vertices are BEV, BVE, EBV, EVB, VBE , and VEB . These would correspond to the 6 cycles:

1: T → B → E → V → T

2: T → B → V → E → T

3: T → E → B → V → T

4: T → E → V → B → T

5: T → V → B → E → T

6: T → V → E → B → T

Step 3: Find the weight of each path. You can reduce your work by observing the cycles that are reverses of each other.

1: 84 + 410 + 207 + 396 = 1097 84 + 410 + 207 + 396 = 1097

2: 84 + 396 + 207 + 370 = 1071 84 + 396 + 207 + 370 = 1071

3: 370 + 410 + 396 + 396 = 1572 370 + 410 + 396 + 396 = 1572

4: Reverse of cycle 2, 1071

5: Reverse of cycle 3, 1572

6: Reverse of cycle 1, 1097

Step 4: Identify a Hamilton cycle of least weight.

The second path, T → B → V → E → T , and its reverse, T → E → V → B → T , have the least weight. The solution is that the officer should travel from Travis Air Force base to Beal Air Force Base, to Vandenberg Air Force base, to Edwards Air Force base, and return to Travis Air Force base, or the same route in reverse.

Your Turn 12.44

Now suppose that the officer needed a cycle that visited all 5 of the Air Force bases in Figure 12.194 . There would be ( 5 − 1 ) ! = 4 ! = 4 × 3 × 2 × 1 = 24 ( 5 − 1 ) ! = 4 ! = 4 × 3 × 2 × 1 = 24 different arrangements of vertices and ( 5 − 1 ) ! 2 = 4 ! 2 = 24 2 = 12 ( 5 − 1 ) ! 2 = 4 ! 2 = 24 2 = 12 distances to compare using the brute force method. If you consider 10 Air Force bases, there would be ( 10 − 1 ) ! = 9 ! = 9 ⋅ 8 ⋅ 7 ⋅ 6 ⋅ 5 ⋅ 4 ⋅ 3 ⋅ 2 ⋅ 1 = 362 , 880 ( 10 − 1 ) ! = 9 ! = 9 ⋅ 8 ⋅ 7 ⋅ 6 ⋅ 5 ⋅ 4 ⋅ 3 ⋅ 2 ⋅ 1 = 362 , 880 different arrangements and ( 10 − 1 ) ! 2 = 9 ! 2 = 9 ⋅ 8 ⋅ 7 ⋅ 6 ⋅ 5 ⋅ 4 ⋅ 3 ⋅ 2 ⋅ 1 2 = 181 , 440 ( 10 − 1 ) ! 2 = 9 ! 2 = 9 ⋅ 8 ⋅ 7 ⋅ 6 ⋅ 5 ⋅ 4 ⋅ 3 ⋅ 2 ⋅ 1 2 = 181 , 440 distances to consider. There must be another way!

The Nearest Neighbor Method

When the brute force method is impractical for solving a traveling salesperson problem, an alternative is a greedy algorithm known as the nearest neighbor method , which always visit the closest or least costly place first. This method finds a Hamilton cycle of relatively low weight in a complete graph in which, at each phase, the next vertex is chosen by comparing the edges between the current vertex and the remaining vertices to find the lowest weight. Since the nearest neighbor method is a greedy algorithm, it usually doesn’t give the best solution, but it usually gives a solution that is "good enough." Most importantly, the number of steps will be the number of vertices. That’s right! A problem with 10 vertices requires 10 steps, not 362,880. Let’s look at an example to see how it works.

Suppose that a candidate for governor wants to hold rallies around the state. They plan to leave their home in city A , visit cities B, C, D, E , and F each once, and return home. The airfare between cities is indicated in the graph in Figure 12.196 .

Let’s help the candidate keep costs of travel down by applying the nearest neighbor method to find a Hamilton cycle that has a reasonably low weight. Begin by marking starting vertex as V 1 V 1 for "visited 1st." Then to compare the weights of the edges between A and vertices adjacent to A : $250, $210, $300, $200, and $100 as shown in Figure 12.197 . The lowest of these is $100, which is the edge between A and F .

Mark F as V 2 V 2 for "visited 2nd" then compare the weights of the edges between F and the remaining vertices adjacent to F : $170, $330, $150 and $350 as shown in Figure 12.198 . The lowest of these is $150, which is the edge between F and D .

Mark D as V 3 V 3 for "visited 3rd." Next, compare the weights of the edges between D and the remaining vertices adjacent to D : $120, $310, and $270 as shown in Figure 12.199 . The lowest of these is $120, which is the edge between D and B .

So, mark B as V 4 V 4 for "visited 4th." Finally, compare the weights of the edges between B and the remaining vertices adjacent to B : $160 and $220 as shown in Figure 12.200 . The lower amount is $160, which is the edge between B and E .

Now you can mark E as V 5 V 5 and mark the only remaining vertex, which is C , as V 6 V 6 . This is shown in Figure 12.201 . Make a note of the weight of the edge from E to C , which is $180, and from C back to A , which is $210.

The Hamilton cycle we found is A → F → D → B → E → C → A . The weight of the circuit is $ 100 + $ 150 + $ 120 + $ 160 + $ 180 + $ 210 = $ 920 $ 100 + $ 150 + $ 120 + $ 160 + $ 180 + $ 210 = $ 920 . This may or may not be the route with the lowest cost, but there is a good chance it is very close since the weights are most of the lowest weights on the graph and we found it in six steps instead of finding 120 different Hamilton cycles and calculating 60 weights. Let’s summarize the procedure that we used.

Step 1: Select the starting vertex and label V 1 V 1 for "visited 1st." Identify the edge of lowest weight between V 1 V 1 and the remaining vertices.

Step 2: Label the vertex at the end of the edge of lowest weight that you found in previous step as V n V n where the subscript n indicates the order the vertex is visited. Identify the edge of lowest weight between V n V n and the vertices that remain to be visited.

Step 3: If vertices remain that have not been visited, repeat Step 2. Otherwise, a Hamilton cycle of low weight is V 1 → V 2 → ⋯ → V n → V 1 V 1 → V 2 → ⋯ → V n → V 1 .

Example 12.45

Using the nearest neighbor method.

Suppose that the candidate for governor wants to hold rallies around the state but time before the election is very limited. They would like to leave their home in city A , visit cities B , C , D , E , and F each once, and return home. The airfare between cities is not as important as the time of travel, which is indicated in Figure 12.202 . Use the nearest neighbor method to find a route with relatively low travel time. What is the total travel time of the route that you found?

Step 1: Label vertex A as V 1 V 1 . The edge of lowest weight between A and the remaining vertices is 85 min between A and D .

Step 2: Label vertex D as V 2 V 2 . The edge of lowest weight between D and the vertices that remain to be visited, B, C, E , and F , is 70 min between D and F .

Repeat Step 2: Label vertex F as V 3 V 3 . The edge of lowest weight between F and the vertices that remain to be visited, B, C, and E , is 75 min between F and C .

Repeat Step 2: Label vertex C as V 4 V 4 . The edge of lowest weight between C and the vertices that remain to be visited, B and E , is 100 min between C and B .

Repeat Step 2: Label vertex B as V 5 V 5 . The only vertex that remains to be visited is E . The weight of the edge between B and E is 95 min.

Step 3: A Hamilton cycle of low weight is A → D → F → C → B → E → A . So, a route of relatively low travel time is A to D to F to C to B to E and back to A . The total travel time of this route is: 85 min + 70 min + 75 min + 100 min + 95 min + 90 min = 515 min or 8 hrs 35 min 85 min + 70 min + 75 min + 100 min + 95 min + 90 min = 515 min or 8 hrs 35 min

Your Turn 12.45

Check your understanding, section 12.9 exercises.

As an Amazon Associate we earn from qualifying purchases.

This book may not be used in the training of large language models or otherwise be ingested into large language models or generative AI offerings without OpenStax's permission.

Want to cite, share, or modify this book? This book uses the Creative Commons Attribution License and you must attribute OpenStax.

Access for free at https://openstax.org/books/contemporary-mathematics/pages/1-introduction

• Authors: Donna Kirk
• Publisher/website: OpenStax
• Book title: Contemporary Mathematics
• Publication date: Mar 22, 2023
• Location: Houston, Texas
• Book URL: https://openstax.org/books/contemporary-mathematics/pages/1-introduction
• Section URL: https://openstax.org/books/contemporary-mathematics/pages/12-9-traveling-salesperson-problem

© Dec 21, 2023 OpenStax. Textbook content produced by OpenStax is licensed under a Creative Commons Attribution License . The OpenStax name, OpenStax logo, OpenStax book covers, OpenStax CNX name, and OpenStax CNX logo are not subject to the Creative Commons license and may not be reproduced without the prior and express written consent of Rice University.

• Coding Problems

Travelling Salesman Problem (TSP)

Problem statement, example 1: travelling salesman problem, example 2: travelling salesman problem, 1. simple approach, c++ code implementation, java code implementation, python code implementation, 2. travelling salesman problem using dynamic programming, c code implementation, 3. greedy approach, practice questions, frequently asked questions, 1. which algorithm is used for the travelling salesman problem, 2. what is the complexity of the travelling salesman problem, 3. how is this problem modelled as a graph problem, 4: what is the difficulty level of the travelling salesman problem.

Travelling Salesman Problem (TSP) – Given a set of cities and the distance between every pair of cities as an adjacency matrix, the problem is to find the shortest possible route that visits every city exactly once and returns to the starting point. The ultimate goal is to minimize the total distance travelled, forming a closed tour or circuit.

The TSP is referred to as an NP-hard problem, meaning there is no known algorithm to solve it in polynomial time for large instances. As the number of cities increases, the number of potential solutions grows exponentially, making an exhaustive search unfeasible. This complexity is one of the reasons why the TSP remains a popular topic of research. Learn More .

Input –

Confused about your next job?

Output –

Here, the TSP Tour is 0-2-1-3-0 and the cost of the tour is 48.

Minimum weight Hamiltonian Cycle : EACBDE= 32

Wondering how the Hamiltonian Cycle Problem and the Traveling Salesman Problem differ? The Hamiltonian Cycle problem is to find out if there exists a tour that visits each city exactly once. Here, we know that the Hamiltonian Tour exists (due to the graph being complete), and there are indeed many such tours. The problem is to find a minimum weight Hamiltonian Cycle.

There are various approaches to finding the solution to the travelling salesman problem- simple (naïve) approach, dynamic programming approach, and greedy approach. Let’s explore each approach in detail:

• Consider city 1 as the starting and ending point. Since the route is cyclic, we can consider any point as a starting point.
• Now, we will generate all possible permutations of cities which are (n-1)!.
• Find the cost of each permutation and keep track of the minimum cost permutation.
• Return the permutation with minimum cost.
• Time complexity: O(N!), Where N is the number of cities.
• Space complexity: O(1).

In the travelling salesman problem algorithm, we take a subset N of the required cities that need to be visited, the distance among the cities dist, and starting cities s as inputs. Each city is identified by a unique city id which we say like 1,2,3,4,5………n

Here we use a dynamic approach to calculate the cost function Cost(). Using recursive calls, we calculate the cost function for each subset of the original problem.

To calculate the cost(i) using Dynamic Programming , we need to have some recursive relation in terms of sub-problems.

We start with all subsets of size 2 and calculate C(S, i) for all subsets where S is the subset, then we calculate C(S, i) for all subsets S of size 3 and so on.

There are at most O(n2^n) subproblems, and each one takes linear time to solve. The total running time is, therefore, O(n^22^n). The time complexity is much less than O(n!) but still exponential. The space required is also exponential.

• Time Complexity: O(N^2*2^N).
• First of them is a list that can hold the indices of the cities in terms of the input matrix of distances between cities
• And the Second one is the array which is our result
• Perform traversal on the given adjacency matrix tsp[][] for all the cities and if the cost of reaching any city from the current city is less than the current cost update the cost.
• Generate the minimum path cycle using the above step and return their minimum cost.
• Time complexity: O(N^2*logN), Where N is the number of cities.
• Space complexity: O(N).
• City Tour Problem
• Shortest Common Substring

Ans . Travelling Salesman Problem uses Dynamic programming with a masking algorithm.

Ans.: The complexity of TSP using Greedy will be O(N^2 LogN) and using DP will be O(N^2 2^N).

Ans .: The TSP can be modelled as a graph problem by considering a complete graph G = (V, E). A tour is then a circuit in G that meets every node. In this context, tours are sometimes called Hamiltonian circuits.

Ans.: It is an NP-hard problem.

• Travelling Salesman Problem

Previous Post

Longest common subsequence, minimum spanning tree – kruskal algorithm.

• Interview Q

DAA Tutorial

Asymptotic analysis, analysis of sorting, divide and conquer, lower bound theory, sorting in linear time, binary search trees, red black tree, dynamic programming, greedy algorithm, backtracking, shortest path, all-pairs shortest paths, maximum flow, sorting networks, complexity theory, approximation algo, string matching.

Interview Questions

• Send your Feedback to [email protected]

Help Others, Please Share

Learn Latest Tutorials

Transact-SQL

Reinforcement Learning

R Programming

React Native

Python Design Patterns

Python Pillow

Python Turtle

Preparation

Verbal Ability

Company Questions

Trending Technologies

Artificial Intelligence

Cloud Computing

Data Science

Machine Learning

B.Tech / MCA

Data Structures

Operating System

Computer Network

Compiler Design

Computer Organization

Discrete Mathematics

Ethical Hacking

Computer Graphics

Software Engineering

Web Technology

Cyber Security

C Programming

Control System

Data Mining

Data Warehouse

Key Products

• Route Optimization API

Optimize routing, task allocation and dispatch

• Directions and Distance Matrix API

Calculate accurate ETAs, distances and directions

• Navigation API & SDKs

Provide turn-by-turn navigation instructions

• Live Tracking API & SDKs

Track and manage assets in real time

• All Products

Product Demos

See NextBillion.ai APIs & SDKs In action

• Integrations

Easily integrate our products with your tools

Platform Overview

Learn about how Nextbillion.ai's platform is designed

Is NextBillion.ai right for you?

Understand if NextBillion.ai is right for your business

NextBillion.ai vs. Google Cloud Fleet Routing

NextBillion.ai vs. Google Distance Matrix API

NextBillion.ai vs. HERE Technologies

Technical Documentation

Snap-to-Road API

Snap GPS tracks to underlying road networks

Isochrone API

Define serviceable areas based on travel times

Optimization

Clustering API

Group data points based on their characteristics

Geofencing API

Mark virtual boundaries & track asset movements

Live Tracking SDK

Real-Time asset tracking on Mobile

Maptiles API

Create immersive visual experience for your customers

Maptiles SDK

Tailor-Made Maps for Mobile Apps

Supply Chain and Logistics

• On-Demand Delivery
• Fleet Management

E-commerce Logistics

• Field Services

Pest Control

Cleaning Services

HVAC Services

Laundry and Dry Cleaning

Ride-Hailing

Urban Mobility

Non Emergency Medical Transport

Employee Transportation

Final Mile Logistics

Public Services

Emergency Services

Waste Management

Supply Chain & Logistics

Get regulation-compliant truck routes

Solve fleet tracking, routing and navigation

• Last-Mile Delivery

Maximize fleet utilization with optimal routes

Real-time ETA calculation

• Middle Mile Delivery

Real-time ETA Calculation

• Ride Hailing

Optimized routes for cab services

• Non-Emergency Medical Transport

Optimize routing and dispatch

Field Workforce

Automate field service scheduling

• Waste Collection

Efficient route planning with road restrictions

See NextBillion.ai APIs & SDKs in Action

• Case Studies

Discover what customers are building in real time with NextBillion.ai

Join us on our upcoming virtual webinars

Whitepapers

Read through expert insights and opinions from the mapping community

Get in-depth and detailed insights

• Product Updates

Latest product releases and enhancements

Navigate the spatial world with engaging and informative content

Experience a more powerful optimization and scheduling platform, better optimized routes, advanced integration capabilities and flexible pricing with NextBillion.ai.

• NextBillion.ai vs Google Cloud Fleet Routing
• NextBillion.ai vs Google Distance Matrix API
• NextBillion.ai vs HERE Technologies

FEATURED BLOG

• API Documentation

Comprehensive API guides and references

Interactive API examples

Integrate tools you use to run your business

• Technical Blogs

Deep-dive into the technical details

Get quick answers to common queries

FEATURED TECHNICAL BLOG

How to Implement Route Optimization API using Python

Learn how to implement route optimization for vehicle fleet management using python in this comprehensive tutorial.

NEXTBILLION.AI

Partner with us

Our story, vision and mission

Meet our tribe

Latest scoop on product updates, partnerships and more

Come join us - see open positions

Reach out to us for any product- or media-related queries

For support queries, write to us at

To partner with us, contact us at

For all media-related queries, reach out to us at

For all career-related queries, reach out to us at

• Request a Demo

Table of Contents

Best Algorithms for the Traveling Salesman Problem

• March 15, 2024

What is a Traveling Salesman Problem?

In the field of combinatorial optimization, the Traveling Salesman Problem (TSP) is a well-known puzzle with applications ranging from manufacturing and circuit design to logistics and transportation. The goal of cost-effectiveness and efficiency has made it necessary for businesses and industries to identify the best TSP solutions. It’s not just an academic issue, either. Using route optimization algorithms to find more profitable routes for delivery companies also lowers greenhouse gas emissions since fewer miles are traveled.

In this technical blog, we’ll examine some top algorithms for solving the Traveling Salesman Problem and describe their advantages, disadvantages, and practical uses.

Explore NextBillion.ai’s Route Optimization API , which uses advanced algorithms to solve TSP in real-world scenarios.

Brute Force Algorithm

The simplest method for solving the TSP is the brute force algorithm. It includes looking at every way the cities could be scheduled and figuring out how far away each approach is overall. Since it ensures that the best solution will be found, it is not useful for large-scale situations due to its time complexity, which increases equally with the number of cities.

This is a detailed explanation of how the TSP is solved by the brute force algorithm:

Create Every Permutation: Make every combination of the cities that is possible. There are a total of n! permutations to think about for n cities. Every combination shows a possible sequence where the salesman could visit the cities.

Determine the Total Distance for Every Combination: Add up the distances between each city in the permutation to find the overall distance traveled for each one. To finish the trip, consider the time from the final city to the starting point.

Determine the Best Option: Observe which permutation produces the smallest total distance and record it. This permutation represents the ideal tour. Return the most effective permutation to the TSP as the solution after examining every option.

Give back the best answer possible: Return the most effective permutation to the TSP as the solution after all possible combinations have been examined.

Even though this implementation gives an exact solution for the TSP, it becomes costly to compute for larger instances due to its time complexity, which increases factorially with the number of cities. 

The Branch-and-Bound Method

The Branch-and-Bound method can be used to solve the Traveling Salesman Problem (TSP) and other combinatorial optimization problems. To effectively find a suitable space and the best answer, divide-and-conquer strategies are combined with eliminating less-than-ideal solutions.

This is how the Branch and Bound method for the Traveling Salesman Problem works:

Start : First, give a simple answer. You could find this by starting with an empty tour or using a heuristic method.

Limit Calculation : Find the lowest total cost of the current partial solution. This limit shows the least amount of money needed to finish the tour.

Divide : Select a variable that is associated with the subsequent stage of the tour. This could mean picking out the next city to visit.

When making branches, think about the possible values for the variable you’ve chosen. Each branch stands for a different choice or option.

Cutting down : If a branch’s lower bound is higher than the best-known solution right now, cut it because you know that it can’t lead to the best solution.

Exploration : Keep using the branch-and-bound method to look into the other branches. Keep cutting and branching until all of your options have been thought through.

New Ideal Solution : Save the best solution you found while doing research. You should change the known one if a new, cheaper solution comes along.

Termination : Continue investigating until all possible paths have been considered and no more choices exist that could lead to a better solution. End the algorithm when all possible outcomes have been studied.

Selecting the order in which to visit the cities is one of the decision variables for the Traveling Salesman Problem. Usually, methods like the Held-Karp lower bound are used to calculate the lower bound. The technique identifies and cuts branches that are likely to result in less-than-ideal solutions as it carefully investigates various combinations of cities.

The Nearest Neighbor Method

A heuristic algorithm called the Nearest Neighbor method estimates solutions to the Traveling Salesman Problem (TSP). In contrast to exact methods like brute force or dynamic programming, which always get the best results, the Nearest Neighbor method finds a quick and reasonable solution by making local, greedy choices.

Here is a detailed explanation of how the nearest-neighbor method solves the TSP problem:

Starting Point : Pick a city randomly to be the tour’s starting point.

Picking Something Greedy: Select the next city on the tour to visit at each stage based on how close the current city is to the not-explored city. Usually, a selected measurement is used to calculate the distance between cities (e.g., Euclidean distance).

Go and Mark: Visit the closest city you picked, add it to your tour, and mark it as observed.

Additionally: Continue this manner until every city has been visited at least once.

Go Back to the Beginning City: After visiting all the other cities, return to the starting city to finish the tour. 

The nearest-neighbor method’s foundation is making locally optimal choices at each stage and hoping that the sum of these choices will produce a reasonable overall solution. Compared to exact algorithms, this greedy approach drastically lowers the level of computation required, which makes it appropriate for relatively large cases of the TSP.

Ant Colony Optimization

ACO, or Ant Colony Optimization, is a metaheuristic algorithm that draws inspiration from ants’ seeking habits. It works very well for resolving a combination of optimization issues, such as the TSP (Traveling Salesman Problem). The idea behind ACO is to imitate ant colonies’ chemical trail communication to determine the best routes.

Ant Colony Optimization provides the following solution for the Traveling Salesman Problem:

Starting Point: A population of synthetic ants should be planted in a random starting city. Every ant is a possible solution for the TSP.

Initialization of The scents: Give each edge in the problem space (connections between cities) an initial amount of synthetic pheromone. The artificial ants communicate with one another via the fragrance. 

Ant Motion: Each ant creates a tour by constantly selecting the next city to visit using a combination of fragrance levels and a heuristic function.

The quantity of fragrance on the edge that links the candidate city to the current city, as well as a heuristic measure that could be based on factors like distance between cities, impact the chances of selecting a specific city.

Ants mimic how real ants use chemical trails for communication by following paths with higher fragrance levels.

Update on Pheromones: The pheromone concentration on every edge is updated once every ant has finished traveling.

The update involves placing fragrances on the borders of the best tours and evaporating existing fragrances to copy the natural breakdown of chemical paths, which is intended to encourage the search for successful paths.

Repetition: For the fixed number of cycles or until a shift standard is satisfied, repeat the steps of ant movement, fragrance update, and tour construction.

Building Solution : After a few iterations, the artificial ants develop an answer, which is considered the algorithm’s outcome. This solution approximates the most efficient TSP tour.

Enhancement: To improve progress and solution quality, the process can be optimized by adjusting parameters like the influence of the heuristic function and the rate at which fragrances evaporate.

Ant Colony Optimization is excellent at solving TSP cases by using the ant population’s group ability. By striking a balance between exploration and exploitation, the algorithm can find potential paths and take advantage of success. It is a well-liked option in the heuristics field since it has been effectively used to solve various optimization issues.

Genetic Algorithm

Genetic Algorithms (GAs) are optimization algorithms derived from the concepts of genetics and natural selection. These algorithms imitate evolution to find predictions for complex problems, such as the Traveling Salesman Problem (TSP). 

Here is how genetic algorithms resolve the TSP:

Starting Point: select a starting group of possible TSP solutions. Every possible tour that visits every city exactly once is represented by each solution.

Assessment: Examine each solution’s fitness within the population. Fitness is commonly defined in the TSP environment as the opposite of the total distance traveled. Tour length is a determining factor in fitness scores.

Choice: Choose people from the population to be the parents of the following generation. Each person’s fitness level determines the likelihood of selection. More fit solutions have a higher chance of being selected.

Transformation (Recombination): To produce offspring, perform crossover, or recombination, on pairs of chosen parents. To create new solutions, crossover entails sharing information between parent solutions.

Crossover can be applied in various ways for TSP, such as order crossover (OX) or partially mapped crossover (PMX), to guarantee that the resulting tours preserve the authenticity of city visits.

Change: Change some of the offspring solutions to introduce arbitrary changes. A mutation can involve flipping two cities or changing the order of a subset of cities.

Mutations add diversity to the population when discovering new regions of the solution space. 

Substitute: Parents and children together make up the new generation of solutions that will replace the old ones. A portion of the top-performing solutions from the previous generation may be retained in the new generation as part of a privileged replacement process.

Finalization: For a predetermined number of generations or until a convergence criterion is satisfied, repeat the selection, crossover, mutation, and replacement processes. 

Enhancement: Modify variables like population size, crossover rate, and mutation rate to maximize the algorithm’s capacity to identify excellent TSP solutions.

When it comes to optimizing combinations, genetic algorithms are exceptional at sifting through big solution spaces and identifying superior answers. Because of their capacity to duplicate natural evolution, they can adjust to the TSP’s structure and find almost ideal tours. GAs are an effective tool in the field of evolutionary computation because they have been successfully applied to a wide range of optimization problems.

NextBillion.ai offers advanced Route Optimization API that solves real-life TSP and VRP problems, which can be easily integrated with your applications. 

Book a demo Today!

In this Article

About author.

Rishabh is a freelance technical writer based in India. He is a technology enthusiast who loves working in the B2B tech space.

It is not possible to solve the Traveling Salesman Problem with Dijkstra’s algorithm. Dijkstra’s algorithm, a single-source shortest path algorithm, finds the shortest possible route from a given source node to every other node in a weighted graph. In comparison, the Traveling Salesman Problem looks for the quickest route that stops in every city exactly once before returning to the starting point.

The term “traveling salesman” refers to a scenario where a salesperson visits different cities to sell goods or services. The goal of this problem is to find the shortest route that goes to each city once and returns to the starting point. It is a fundamental problem in algorithmic optimization to determine the best order of city trips and minimize travel time or distance.

“Route salesman” or just “sales representative” are other terms for a traveling salesman. These people go to various places to sell goods and services to customers. The traveling salesman, who determines the shortest route to visit multiple cities, is often referred to as a “touring agent” or simply as the “salesman” in the context of mathematical optimization.

The minimum distance a salesman needs to visit each city exactly once and then return to the starting city is known as the shortest distance in the Traveling Salesman Problem (TSP). It stands for the ideal tour duration that reduces the total travel distance. The goal of solving the TSP, an essential issue in combinatorial optimization, is finding the shortest distance.

Traveling Salesman Algorithms

From naive to christofide, how to read this article.

Our article was written using a component-based library called Idyll. In addition to buttons and sliders you will see the following in this article... This component is an external link which will redirect you to another page. This component is an internal link which will send you to a part of the page when clicked on. This component is an action link which will trigger some event on the page to do something. Lastly, this article is only supported on Chrome; other browsers have an SVG rendering bug that can show up.

Introduction

Given a list of cities and the distances between each pair of cities, what is the shortest possible route that visits each city exactly once and returns to the origin city?

In essence, this question is asking us (the salesman) to visit each of the cities via the shortest path that gets us back to our origin city. We can conceptualize the TSP as a graph where each city is a node, each node has an edge to every other node, and each edge weight is the distance between those two nodes.

The first computer coded solution of TSP by Dantzig, Fulkerson, and Johnson came in the mid 1950’s with a total of 49 cities. Since then, there have been many algorithmic iterations and 50 years later, the TSP problem has been successfully solved with a node size of 24,978 cities! Multiple variations on the problem have been developed as well, such as mTSP , a generalized version of the problem and Metric TSP , a subcase of the problem.

The original Traveling Salesman Problem is one of the fundamental problems in the study of combinatorial optimization—or in plain English: finding the best solution to a problem from a finite set of possible solutions . This field has become especially important in terms of computer science, as it incorporate key principles ranging from searching, to sorting, to graph theory.

Real World Applications

However, before we dive into the nitty gritty details of TSP, we would like to present some real-world examples of the problem to illustrate its importance and underlying concepts. Applications of the TSP include:

Click on an example to the left for more information!

• Santa delivering presents.
• Fulfilling an order in a warehouse.
• Designing and building printed circuit boards.
• Analyzing an X-Ray.
• GPS satellite systems.
• School bus scheduling.

Finding Solutions – Exact vs. Approximation

The difficulty in solving a combinatorial optimization problem such as the TSP lies not in discovering a single solution, but rather quickly verifying that a given solution is the optimal solution. To verify, without a shadow of a doubt, that a single solution is optimized requires both computing all the possible solutions and then comparing your solution to each of them. We will call this solution the Exact solution. The number of computations required to calculate this Exact solution grows at an enormous rate as the number of cities grow as well. For example, the total number of possible paths for 7 cities is just over 5,000 , for 10 cities it is over 3.6 million , and for 13 cities it is over 6 billion . Clearly, this growth rate quickly eclipses the capabilities of modern personal computers and determining an exact solution may be near impossible for a dataset with even 20 cities. We will explore the exact solution approach in greater detail during the Naïve section.

The physical limitations of finding an exact solution lead us towards a very important concept – approximation algorithms . In an approximation algorithm, we cannot guarantee that the solution is the optimal one, but we can guarantee that it falls within a certain proportion of the optimal solution. The real strength of approximation algorithms is their ability to compute this bounded solution in an amount of time that is several orders of magnitude quicker than the exact solution approach. Later on in this article we will explore two different approximation algorithms, Nearest Neighbor and Christofide’s Algorithm , and the many facets of each approach.

The Naïve Approach

We can imagine that from a starting city, there are ∣ V ∣ − 1 |V| - 1 ∣ V ∣ − 1 possibilities for the second city. Following this connection, the second city will then have ∣ V ∣ − 2 |V| - 2 ∣ V ∣ − 2 possibilities, and so on and so on... Since our path is bidirectional, it follows that some cycles we calculate at will be disposible as they are duplicates if reversed. Thus we arrive at ( ∣ V ∣ − 1 ) ! / 2 (|V| - 1)!/2 ( ∣ V ∣ − 1 ) ! / 2 possible paths.

This figure can better be expressed as having a bound O ( ∣ V ∣ ! ) O(|V|!) O ( ∣ V ∣ ! ) possible paths. As explored above, a factorial upper bound is simply far too great for real applications.

Nearest Neighbor

Choose the next city in the path to be the closest city that you have not already visited. Once all cities have been visited, the salesman return home.

Next: Click here for a quick walkthrough of the algorithm!

Christofides Algorithm

Steps: Intro MST Odd Vertices Matches Eulerian Hamiltonian

This section is meant to serve as a “slide show” that will walk you through the previously outlined 5 steps of Christofides’ Algorithm. At each step after this one you will be able to switch between a Small Dataset , Medium Dataset , and Large Dataset , Clear the edges in the graph, and move to the previous step and Next Step in the algorithm.

In addition, each step can be accessed by clicking its corresponding button underneath the map to the right. Next Step: Minimum Spanning Tree

Algorithm Analysis

While the Naïve and dynamic programming approaches always calculate the exact solution, it comes at the cost of enormous runtime; datasets beyond 15 vertices are too large for personal computers. The most common approximation algorithm, Nearest Neighbor, can produce a very good result (within 25% of the exact solution) for most cases, however it has no guarantee on its error bound. That said, Christofides algorithm has the current best error bound of within 50% of the exact solution for approximation algorithms. Christofides produces this result in a “good” runtime compared to Naïve and dynamic, but it still significantly slower than the Nearest Neighbor approach.

In the chart above the runtimes of the naive, dynamic programming, nearest neighbors, and Christofides’ are plotted. The x-axis represents the number of cities that the algorithm works on while the y-axis represents the worst-case amount of calculations it will need to make to get a solution. As you can see, as the number of cities increases every algorithm has to do more calculations however naive will end up doing significantly more. Note how with 20 cities, the naive algorithm is 5,800,490,399 times slower than even the minimally faster dynamic programming algorithm.

Closing Thoughts

We would like to thank Dr. Heer, Matthew Conlen, Younghoon Kim, and Kaitlyn Zhou for their contributions to CSE 442, the UW Interactive Data Lab, Idyll, and much more. This article would not have been possible without their support and guidance.

Sources, References, and Links:

Inspiration from Idyll articles: Flight, Barnes Hut

Algorithms for the Travelling Salesman Problem

Printables.com

• The Travelling Salesman Problem (TSP) is a classic algorithmic problem in the field of computer science and operations research, focusing on optimization. It seeks the shortest possible route that visits every point in a set of locations just once.
• The TSP problem is highly applicable in the logistics sector , particularly in route planning and optimization for delivery services. TSP solving algorithms help to reduce travel costs and time.
• Real-world applications often require adaptations because they involve additional constraints like time windows, vehicle capacity, and customer preferences.
• Advances in technology and algorithms have led to more practical solutions for real-world routing problems. These include heuristic and metaheuristic approaches that provide good solutions quickly.
• Tools like Routific use sophisticated algorithms and artificial intelligence to solve TSP and other complex routing problems, transforming theoretical solutions into practical business applications.

The Traveling Salesman Problem (TSP) is the challenge of finding the shortest path or shortest possible route for a salesperson to take, given a starting point, a number of cities (nodes), and optionally an ending point. It is a well-known algorithmic problem in the fields of computer science and operations research, with important real-world applications for logistics and delivery businesses.

There are obviously a lot of different routes to choose from, but finding the best one — the one that will require the least distance or cost — is what mathematicians and computer scientists have spent decades trying to solve.

It’s much more than just an academic problem in graph theory. Finding more efficient routes using route optimization algorithms increases profitability for delivery businesses, and reduces greenhouse gas emissions because it means less distance traveled.

In theoretical computer science, the TSP has commanded so much attention because it’s so easy to describe yet so difficult to solve. The TSP is known to be a combinatorial optimization problem that’s an NP-hard problem, which means that the number of possible solution sequences grows exponential with the number of cities. Computer scientists have not found any algorithm for solving travelling salesman problems in polynomial time, and therefore rely on approximation algorithms to try numerous permutations and select the shortest route with the minimum cost.

The main problem can be solved by calculating every permutation using a brute force approach, and selecting the optimal solution. However, as the number of destinations increases, the corresponding number of roundtrips grows exponentially, soon surpassing the capabilities of even the fastest computers. With 10 destinations, there can be more than 300,000 roundtrip permutations. With 15 destinations, the number of possible routes could exceed 87 billion.

For larger real-world travelling salesman problems, when manual methods such as Google Maps Route Planner or Excel route planner no longer suffice, businesses rely on approximate solutions that are sufficiently optimized by using fast tsp algorithms that rely on heuristics. Finding the exact optimal solution using dynamic programming is usually not practical for large problems.

Three popular Travelling Salesman Problem Algorithms

Here are some of the most popular solutions to the Travelling Salesman Problem:

1. The brute-force approach

TThe brute-force approach, also known as the naive approach, calculates and compares all possible permutations of routes or paths to determine the shortest unique solution. To solve the TSP using the brute-force approach, you must calculate the total number of routes and then draw and list all the possible routes. Calculate the distance of each route and then choose the shortest one — this is the optimal solution. 

This is only feasible for small problems, rarely useful beyond theoretical computer science tutorials.

2. The branch and bound method

The branch and bound algorithm starts by creating an initial route, typically from the starting point to the first node in a set of cities. Then, it systematically explores different permutations to extend the route beyond the first pair of cities, one node at a time. Each time a new node is added, the algorithm calculates the current path's length and compares it to the optimal route found so far. If the current path is already longer than the optimal route, it "bounds" or prunes that branch of the exploration, as it would not lead to a more optimal solution.

This pruning is the key to making the algorithm efficient. By discarding unpromising paths, the search space is narrowed down, and the algorithm can focus on exploring only the most promising paths. The process continues until all possible routes are explored, and the shortest one is identified as the optimal solution to the traveling salesman problem. Branch and bound is an effective greedy approach for tackling NP-hard optimization problems like the traveling salesman problem.

3. The nearest neighbor method

To implement the nearest neighbor algorithm, we begin at a randomly selected starting point. From there, we find the closest unvisited node and add it to the sequencing. Then, we move to the next node and repeat the process of finding the nearest unvisited node until all nodes are included in the tour. Finally, we return to the starting city to complete the cycle.

While the nearest neighbor approach is relatively easy to understand and quick to execute, it rarely finds the optimal solution for the traveling salesperson problem. It can be significantly longer than the optimal route, especially for large and complex instances. Nonetheless, the nearest neighbor algorithm serves as a good starting point for tackling the traveling salesman problem and can be useful when a quick and reasonably good solution is needed.

This greedy algorithm can be used effectively as a way to generate an initial feasible solution quickly, to then feed into a more sophisticated local search algorithm, which then tweaks the solution until a given stopping condition. ‍

How route optimization algorithms work to solve the Travelling Salesman Problem.

Academic tsp solutions.

Academics have spent years trying to find the best solution to the Travelling Salesman Problem The following solutions were published in recent years:

• Machine learning speeds up vehicle routing : MIT researchers apply Machine Learning methods to solve large np-complete problems by solving sub-problems.
• Zero Suffix Method : Developed by Indian researchers, this method solves the classical symmetric TSP. 
• Biogeography‐based Optimization Algorithm : This method is designed based on the animals’ migration strategy to solve the problem of optimization. 
• Meta-Heuristic Multi Restart Iterated Local Search (MRSILS): The proponents of this research asserted that the meta-heuristic MRSILS is more efficient than the Genetic Algorithms when clusters are used. 
• Multi-Objective Evolutionary Algorithm : This method is designed for solving multiple TSP based on NSGA-II. 
• Multi-Agent System : This system is designed to solve the TSP of N cities with fixed resource. 

Real-world TSP applications

Despite the complexity of solving the Travelling Salesman Problem, approximate solutions — often produced using artificial intelligence and machine learning — are useful in all verticals.

For example, TSP solutions can help the logistics sector improve efficiency in the last mile. Last mile delivery is the final link in a supply chain, when goods move from a transportation hub, like a depot or a warehouse, to the end customer. Last mile delivery is also the leading cost driver in the supply chain. It costs an average of $10.1, but the customer only pays an average of $8.08 because companies absorb some of the cost to stay competitive. So bringing that cost down has a direct effect on business profitability.

Minimizing costs in last mile delivery is essentially a Vehicle Routing Problem (VRP). VRP, a generalized version of the travelling salesman problem, is one of the most widely studied problems in mathematical optimization. Instead of one best path, it deals with finding the most efficient set of routes or paths. The problem may involve multiple depots, hundreds of delivery locations, and several vehicles. As with the travelling salesman problem, determining the best solution to VRP is NP-complete.

Real-life TSP and VRP solvers

While academic solutions to TSP and VRP aim to provide the optimal solution to these NP-hard problems, many of them aren’t practical when solving real world problems, especially when it comes to solving last mile logistical challenges.

That’s because academic solvers strive for perfection and thus take a long time to compute the optimal solutions – hours, days, and sometimes years. If a delivery business needs to plan daily routes, they need a route solution within a matter of minutes. Their business depends on delivery route planning software so they can get their drivers and their goods out the door as soon as possible. Another popular alternative is to use Google maps route planner .

Real-life TSP and VRP solvers use route optimization algorithms that find near-optimal solutions in a fraction of the time, giving delivery businesses the ability to plan routes quickly and efficiently.

If you want to know more about real-life TSP and VRP solvers, check out the resources below 👇

Route Optimization API - TSP Solver

Route Optimization API - VRP Solver

Frequently Asked Questions

What is a hamiltonian cycle, and why is it important in solving the travelling salesman problem.

A Hamiltonian cycle is a complete loop that visits every vertex in a graph exactly once before returning to the starting vertex. It's crucial for the TSP because the problem essentially seeks to find the shortest Hamiltonian cycle that minimizes travel distance or time.

What role does linear programming play in solving the Travelling Salesman Problem?

Linear programming (LP) is a mathematical method used to optimize a linear objective function, subject to linear equality and inequality constraints. In the context of TSP, LP can help in formulating and solving relaxation of the problem to find bounds or approximate solutions, often by ignoring the integer constraints (integer programming being a subset of LP) to simplify the problem.

What is recursion, and how does it apply to the Travelling Salesman Problem?

Recursion involves a function calling itself to solve smaller sub-problems of the same type as the larger problem. In TSP, recursion is used in methods like the "Divide and Conquer" strategy, breaking down the problem into smaller, manageable subsets, which can be particularly useful in dynamic programming solutions. It reduces redundancy and computation time, making the problem more manageable.

Why is understanding time complexity important when studying the Travelling Salesman Problem?

Time complexity refers to the computational complexity that describes the amount of computer time it takes to solve a problem. For TSP, understanding time complexity is crucial because it helps predict the performance of different algorithms, especially given that TSP is NP-hard and solutions can become impractically slow as the number of cities increases.

Related articles

Liked this article? See below for more recommended reading!

Solving the Vehicle Routing Problem (2024)

How To Optimize Multi-Stop Routes With Google Maps (2024)

How Route Optimization Impacts Our Earth

Traveling Salesman Problem and Approximation Algorithms

One of my research interests is a graphical model structure learning problem in multivariate statistics. I have been recently studying and trying to borrow ideas from approximation algorithms, a research field that tackles difficult combinatorial optimization problems. This post gives a brief introduction to two approximation algorithms for the (metric) traveling salesman problem: the double-tree algorithm and Christofides’ algorithm. The materials are mainly based on §2.4 of Williamson and Shmoys (2011).

1. Approximation algorithms

In combinatorial optimization, most interesting problems are NP-hard and do not have polynomial-time algorithms to find optimal solutions (yet?). Approximation algorithms are efficient algorithms that find approximate solutions to such problems. Moreover, they give provable guarantees on the distance of the approximate solution to the optimal ones.

We assume that there is an objective function associated with an optimization problem. An optimal solution to the problem is one that minimizes the value of this objective function. The value of the optimal solution is often denoted by \(\mathrm{OPT}\).

An \(\alpha\)-approximation algorithm for an optimization problem is a polynomial-time algorithm that for all instances of the problem produces a solution, whose value is within a factor of \(\alpha\) of \(\mathrm{OPT}\), the value of an optimal solution. The factor \(\alpha\) is called the approximation ratio.

2. Traveling salesman problem

The traveling salesman problem (TSP) is NP-hard and one of the most well-studied combinatorial optimization problems. It has broad applications in logistics, planning, and DNA sequencing. In plain words, the TSP asks the following question:

Given a list of cities and the distances between each pair of cities, what is the shortest possible route that visits each city and returns to the origin city?

Formally, for a set of cities \([n] = \{1, 2, \ldots, n \}\), an \(n\)-by-\(n\) matrix \(C = (c_{ij})\), where \(c_{ij} \geq 0 \) specifies the cost of traveling from city \(i\) to city \(j\). By convention, we assume \(c_{ii} = 0\) and \(c_{ij} = c_{ji}\), meaning that the cost of traveling from city \(i\) to city \(j\) is equal to the cost of traveling from city \(j\) to city \(i\). Furthermore, we only consider the metric TSP in this article; that is, the triangle inequality holds for any \(i,j,k\): $$ c_{ik} \leq c_{ij} + c_{jk}, \quad \forall i, j, k \in [n]. $$

Given a permutation \(\sigma\) of \([n]\), a tour traverses the cities in the order \(\sigma(1), \sigma(2), \ldots, \sigma(n)\). The goal is to find a tour with the lowest cost, which is equal to $$ c_{\sigma(n) \sigma(1)} + \sum_{i=1}^{n-1} c_{\sigma(i) \sigma(i+1)}. $$

3. Double-tree algorithm

We first describe a simple algorithm called the double-tree algorithm and prove that it is a 2-approximation algorithm.

Double-tree algorithm Find a minimum spanning tree \(T\). Duplicate the edges of \(T\). Find an Eulerian tour. Shortcut the Eulerian tour.

Figure 1 shows the algorithm on a simple five-city instance. We give a step-by-step explanation of the algorithm.

A spanning tree of an undirected graph is a subgraph that is a tree and includes all of the nodes. A minimum spanning tree of a weighted graph is a spanning tree for which the total edge cost is minimized. There are several polynomial-time algorithms for finding a minimum spanning tree, e.g., Prim’s algorithm , Kruskal’s algorithm , and the reverse-delete algorithm . Figure 1a shows a minimum spanning tree \(T\).

There is an important relationship between the minimum spanning tree problem and the traveling salesman problem.

Lemma 1. For any input to the traveling salesman problem, the cost of the optimal tour is at least the cost of the minimum spanning tree on the same input.

The proof is simple. Deleting any edge from the optimal tour results in a spanning tree, the cost of which is at least the cost of the minimum spanning tree. Therefore, the cost of the minimum spanning tree \(T\) in Figure 1(a) is at most \( \mathrm{OPT}\).

Next, each edge in the minimum spanning tree is replaced by two copies of itself, as shown in Figure 1b. The resulting (multi)graph is Eulerian. A graph is said to be Eulerian if there exists a tour that visits every edge exactly once. A graph is Eulerian if and only if it is connected and each node has an even degree. Given an Eulerian graph, it is easy to construct a traversal of the edges. For example, a possible Eulerian tour in Figure 1b is 1–3–2–3–4–5–4–3–1. Moreover, since the edges are duplicated from the minimum spanning tree, the Eulerian tour has cost at most \(2 , \mathrm{OPT}\).

Finally, given the Eulerian tour, we remove all but the first occurrence of each node in the sequence; this step is called shortcutting . By the triangle inequality, the cost of the shortcut tour is at most the cost of the Eulerian tour, which is not greater than \(2 , \mathrm{OPT}\). In Figure 1c, the shortcut tour is 1–3–2–4–5–1. When going from node 2 to node 4 by omitting node 3, we have \(c_{24} \leq c_{23} + c_{34}\). Similarly, when skipping nodes 4 and 3, \(c_{51} \leq c_{54} + c_{43} + c_{31}\).

Therefore, we have analyzed the approximation ratio of the double-tree algorithm.

Theorem 1. The double-tree algorithm for the metric traveling salesman problem is a 2-approximation algorithm.

4. Christofides' algorithm

The basic strategy of the double-tree algorithm is to construct an Eulerian tour whose total cost is at most \(\alpha , \mathrm{OPT}\), then shortcut it to get an \(\alpha\)-approximation solution. The same strategy can be carried out to yield a 3/2-approximation algorithm.

Christofides' algorithm Find a minimum spanning tree \(T\). Let \(O\) be the set of nodes with odd degree in \(T\). Find a minimum-cost perfect matching \(M\) on \(O\). Add the set of edges of \(M\) to \(T\). Find an Eulerian tour. Shortcut the Eulerian tour.

Figure 2 illustrates the algorithm on a simple five-city instance of TSP.

The algorithm starts again with the minimum spanning tree \(T\). The reason we cannot directly find an Eulerian tour is that its leaf nodes all have degrees of one. However, by the handshaking lemma , there is an even number of odd-degree nodes. If these nodes can be paired up, then it becomes an Eulerian graph and we can proceed as before.

Let \(O\) be the set of odd-degree nodes in \(T\). To pair them up, we want to find a collection of edges that contain each node in \(O\) exactly once. This is called a perfect matching in graph theory. Given a complete graph (on an even number of nodes) with edge costs, there is a polynomial-time algorithm to find the perfect matching of the minimum total cost, known as the blossom algorithm .

For the minimum spanning tree \(T\) in Figure 2a, \( O = \{1, 2, 3, 5\}\). The minimum-cost perfect matching \(M\) on the complete graph induced by \(O\) is shown in Figure 2b. Adding the edges of \(M\) to \(T\), the result is an Eulerian graph, since we have added a new edge incident to each odd-degree node in \(T\). The remaining steps are the same as in the double-tree algorithm.

We want to show that the Eulerian graph has total cost of at most 3/2 \(\mathrm{OPT}\). Since the total cost of the minimum spanning tree \(T\) is at most \(\mathrm{OPT}\), we only need to show that the perfect matching \(M\) has cost at most 1/2 \(\mathrm{OPT}\).

We start with the optimal tour on the entire set of cities, the cost of which is \(\mathrm{OPT}\) by definition. Figure 3a presents a simplified illustration of the optimal tour; the solid circles represent nodes in \(O\). By omitting the nodes that are not in \(O\) from the optimal tour, we get a tour on \(O\), as shown in Figure 3b. By the shortcutting argument again, the total cost of the tour on \(O\) is at most \(\mathrm{OPT}\). Next, color the edges yellow and green, alternating colors as the tour is traversed, as illustrated in Figure 3c. This partitions the edges into two sets: the yellow set and the green set; each is a perfect matching on \(O\). Since the total cost of the two matchings is at most \(\mathrm{OPT}\), the cheaper one has cost at most 1/2 \(\mathrm{OPT}\). In other words, there exists a perfect matching on \(O\) of cost at most 1/2 \(\mathrm{OPT}\). Therefore, the minimum-cost perfect matching must have cost not greater than 1/2 \(\mathrm{OPT}\). This completes the proof of the following theorem.

Theorem 2. Christofides' algorithm for the metric traveling salesman problem is a 3/2-approximation algorithm.

• Williamson, D. P., & Shmoys, D. B. (2011). The Design of Approximation Algorithms. Cambridge University Press.

Written on Feb 10, 2019.

Traveling Salesman Problem with Python: Greedy and Brute Force

Just imagine yourself as a delivery courier. You have to deliver multiple parcels to many different spots. You also aim to minimize the fuel costs and time of traveling to maximize profit. This generally creates confusion about where to deliver parcels first and which routes to take.

In this article, we will learn about the famous problem of Travelling Salesman. We will solve this issue using Python programming language. We will also try to plot the best route to be taken and calculate the minimum distance to be traveled.

Recommended: Connected Health: Exploring IoT Solutions for Healthcare Transformation

Recommended: Delivery Route Optimization using Python: A Step-by-Step Guide

Solving the Traveling Salesman Problem with Python

The problem statement is that a salesman has to travel to the Indian cities of Mumbai, Delhi, Bangalore, Hyderabad, Ahmedabad, Chennai, Kolkata, Surat, Pune, and Jaipur to sell some products.

The objective of the problem is to minimize the total distance travelled by the salesman.

This describes our problem statement. Now let’s move on to how to solve this problem using Python programming language.

We will look at two ways of solving the problem – using the Greedy algorithm and the Brute Force method ( this method is the most preferred one as it provides more optimal solutions ).

Example Usage and Visualization of the Greedy Algorithm

Let us look at the code of the Simple Greedy algorithm.

In the above example, we randomly input some coordinates and calculated the best route. Let us look at the output of this method.

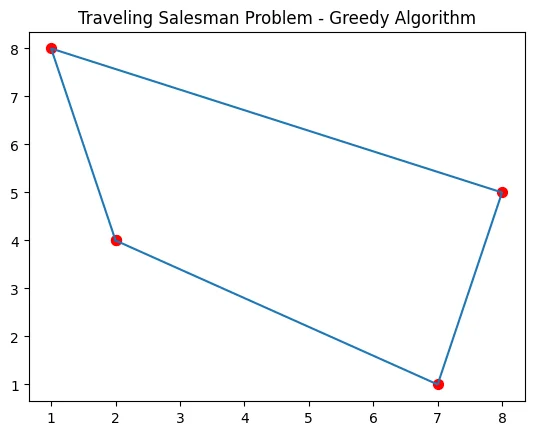
Thus, according to the Greedy algorithm, we will travel to city 1 first, and cities 1,3,2 after that.

Brute Force Approach to the Traveling Salesman Problem

Let us look at the code of the Brute Force Method.

Let us look at the output of the Brute Force method.

Thus, according to the Brute force method, the minimum distance is approximately 230 units.

Greedy Algorithm vs. Brute Force Method

The difference between the Greedy algorithm and the Brute Force method is that the Greedy algorithm builds up the solution step by step whereas in the Brute Force method, all the permutations of the solution are found and then the solution with minimum distance is selected.

Here you go! Now you know the Travelling Salesman Problem and how to solve it using Python. In this article, you learned about two methods of approach i.e. Greedy algorithm and Travelling Salesman problem.

Hope you enjoyed reading it!

Recommended: Backtracking Line Search Algorithm for Unconstrained Optimization

Recommended: Large integer handling in Python (optimization)