what is travelling wave in physics

Travelling Wave

When something about the physical world changes, the information about that disturbance gradually moves outwards, away from the source, in every direction. As the information travels, it travels in the form of a wave. Sound to our ears, light to our eyes, and electromagnetic radiation to our mobile phones are all transported in the form of waves. A good visual example of the propagation of waves is the waves created on the surface of the water when a stone is dropped into a lake. In this article, we will be learning more about travelling waves.

Describing a Wave

A wave can be described as a disturbance in a medium that travels transferring momentum and energy without any net motion of the medium. A wave in which the positions of maximum and minimum amplitude travel through the medium is known as a travelling wave. To better understand a wave, let us think of the disturbance caused when we jump on a trampoline. When we jump on a trampoline, the downward push that we create at a point on the trampoline slightly moves the material next to it downward too.

When the created disturbance travels outward, the point at which our feet first hit the trampoline recovers moving outward because of the tension force in the trampoline and that moves the surrounding nearby materials outward too. This up and down motion gradually ripples out as it covers more area of the trampoline. And, this disturbance takes the shape of a wave.

Following are a few important points to remember about the wave:

• The high points in the wave are known as crests and the low points in the wave are known as troughs.
• The maximum distance of the disturbance of the wave from the mid-point to either the top of the crest or to the bottom of a trough is known as amplitude.
• The distance between two adjacent crests or two adjacent troughs is known as a wavelength and is denoted by 𝛌.
• The time interval of one complete vibration is known as a time period.
• The number of vibrations the wave undergoes in one second is known as a frequency.
• The relationship between the time period and frequency is given as follows:
• The speed of a wave is given by the equation

Different Types of Waves

Different types of waves exhibit distinct characteristics. These characteristics help us distinguish between wave types. The orientation of particle motion relative to the direction of wave propagation is one way the traveling waves are distinguished. Following are the different types of waves categorized based on the particle motion:

• Pulse Waves – A pulse wave is a wave comprising only one disturbance or only one crest that travels through the transmission medium.
• Continuous Waves – A continuous-wave is a waveform of constant amplitude and frequency.
• Transverse Waves – In a transverse wave, the motion of the particle is perpendicular to the direction of propagation of the wave.
• Longitudinal Waves – Longitudinal waves are the waves in which the motion of the particle is in the same direction as the propagation of the wave.

Although they are different, there is one property common between them and that is the transportation of energy. An object in simple harmonic motion has an energy of

Constructive and Destructive Interference

A phenomenon in which two waves superimpose to form a resultant wave of lower, greater, or the same amplitude is known as interference. Constructive and destructive interference occurs due to the interaction of waves that are correlated with each other either because of the same frequency or because they come from the same source. The interference effects can be observed in all types of waves such as gravity waves and light waves.

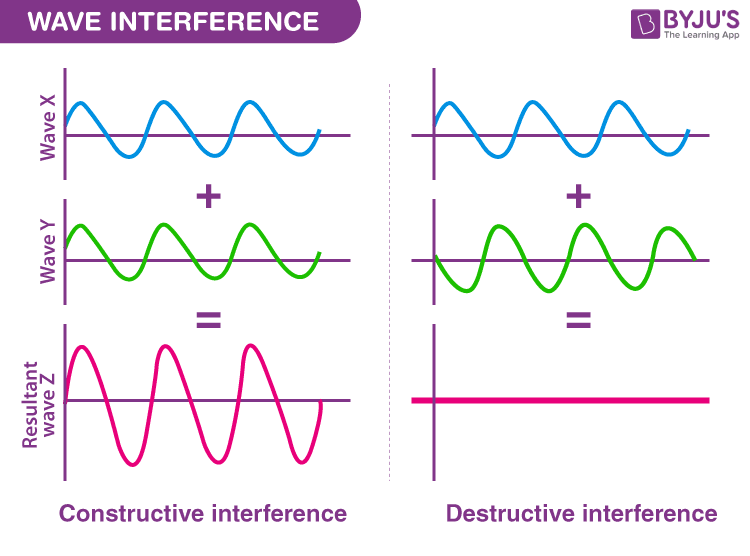
According to the principle of superposition of the waves , when two or more propagating waves of the same type are incidents on the same point, the resultant amplitude is equal to the vector sum of the amplitudes of the individual waves. When a crest of a wave meets a crest of another wave of the same frequency at the same point, then the resultant amplitude is the sum of the individual amplitudes. This type of interference is known as constructive interference. If a crest of a wave meets a trough of another wave, then the resulting amplitude is equal to the difference in the individual amplitudes and this is known as destructive interference.

Stay tuned to BYJU’S to learn more physics concepts with the help of interactive videos.

Watch the video and understand longitudinal and transverse waves in detail.

Frequently Asked Questions – FAQs

What is a pulse wave, what are longitudinal waves, what is superposition of waves, what is electromagnetic radiation, what is constructive interference.

Put your understanding of this concept to test by answering a few MCQs. Click ‘Start Quiz’ to begin!

Select the correct answer and click on the “Finish” button Check your score and answers at the end of the quiz

Visit BYJU’S for all Physics related queries and study materials

Your result is as below

Request OTP on Voice Call

Leave a Comment Cancel reply

Your Mobile number and Email id will not be published. Required fields are marked *

Post My Comment

• Share Share

Register with BYJU'S & Download Free PDFs

Register with byju's & watch live videos.

16.1 Traveling Waves

Learning objectives.

By the end of this section, you will be able to:

• Describe the basic characteristics of wave motion
• Define the terms wavelength, amplitude, period, frequency, and wave speed
• Explain the difference between longitudinal and transverse waves, and give examples of each type
• List the different types of waves

We saw in Oscillations that oscillatory motion is an important type of behavior that can be used to model a wide range of physical phenomena. Oscillatory motion is also important because oscillations can generate waves, which are of fundamental importance in physics. Many of the terms and equations we studied in the chapter on oscillations apply equally well to wave motion ( (Figure) ).

Figure 16.2 From the world of renewable energy sources comes the electric power-generating buoy. Although there are many versions, this one converts the up-and-down motion, as well as side-to-side motion, of the buoy into rotational motion in order to turn an electric generator, which stores the energy in batteries.

Types of Waves

A wave is a disturbance that propagates, or moves from the place it was created. There are three basic types of waves: mechanical waves, electromagnetic waves, and matter waves.

Basic mechanical waves are governed by Newton’s laws and require a medium. A medium is the substance a mechanical waves propagates through, and the medium produces an elastic restoring force when it is deformed. Mechanical waves transfer energy and momentum, without transferring mass. Some examples of mechanical waves are water waves, sound waves, and seismic waves. The medium for water waves is water; for sound waves, the medium is usually air. (Sound waves can travel in other media as well; we will look at that in more detail in Sound .) For surface water waves, the disturbance occurs on the surface of the water, perhaps created by a rock thrown into a pond or by a swimmer splashing the surface repeatedly. For sound waves, the disturbance is a change in air pressure, perhaps created by the oscillating cone inside a speaker or a vibrating tuning fork. In both cases, the disturbance is the oscillation of the molecules of the fluid. In mechanical waves, energy and momentum transfer with the motion of the wave, whereas the mass oscillates around an equilibrium point. (We discuss this in Energy and Power of a Wave .) Earthquakes generate seismic waves from several types of disturbances, including the disturbance of Earth’s surface and pressure disturbances under the surface. Seismic waves travel through the solids and liquids that form Earth. In this chapter, we focus on mechanical waves.

Electromagnetic waves are associated with oscillations in electric and magnetic fields and do not require a medium. Examples include gamma rays, X-rays, ultraviolet waves, visible light, infrared waves, microwaves, and radio waves. Electromagnetic waves can travel through a vacuum at the speed of light, [latex] v=c=2.99792458\,×\,{10}^{8}\,\text{m/s}. [/latex] For example, light from distant stars travels through the vacuum of space and reaches Earth. Electromagnetic waves have some characteristics that are similar to mechanical waves; they are covered in more detail in Electromagnetic Waves in volume 2 of this text.

Matter waves are a central part of the branch of physics known as quantum mechanics. These waves are associated with protons, electrons, neutrons, and other fundamental particles found in nature. The theory that all types of matter have wave-like properties was first proposed by Louis de Broglie in 1924. Matter waves are discussed in Photons and Matter Waves in the third volume of this text.

Mechanical Waves

Mechanical waves exhibit characteristics common to all waves, such as amplitude, wavelength, period, frequency, and energy. All wave characteristics can be described by a small set of underlying principles.

The simplest mechanical waves repeat themselves for several cycles and are associated with simple harmonic motion. These simple harmonic waves can be modeled using some combination of sine and cosine functions. For example, consider the simplified surface water wave that moves across the surface of water as illustrated in (Figure) . Unlike complex ocean waves, in surface water waves, the medium, in this case water, moves vertically, oscillating up and down, whereas the disturbance of the wave moves horizontally through the medium. In (Figure) , the waves causes a seagull to move up and down in simple harmonic motion as the wave crests and troughs (peaks and valleys) pass under the bird. The crest is the highest point of the wave, and the trough is the lowest part of the wave. The time for one complete oscillation of the up-and-down motion is the wave’s period T . The wave’s frequency is the number of waves that pass through a point per unit time and is equal to [latex] f=1\text{/}T. [/latex] The period can be expressed using any convenient unit of time but is usually measured in seconds; frequency is usually measured in hertz (Hz), where [latex] 1\,{\text{Hz}=1\,\text{s}}^{-1}. [/latex]

The length of the wave is called the wavelength and is represented by the Greek letter lambda [latex] (\lambda ) [/latex], which is measured in any convenient unit of length, such as a centimeter or meter. The wavelength can be measured between any two similar points along the medium that have the same height and the same slope. In (Figure) , the wavelength is shown measured between two crests. As stated above, the period of the wave is equal to the time for one oscillation, but it is also equal to the time for one wavelength to pass through a point along the wave’s path.

The amplitude of the wave ( A ) is a measure of the maximum displacement of the medium from its equilibrium position. In the figure, the equilibrium position is indicated by the dotted line, which is the height of the water if there were no waves moving through it. In this case, the wave is symmetrical, the crest of the wave is a distance [latex] \text{+}A [/latex] above the equilibrium position, and the trough is a distance [latex] \text{−}A [/latex] below the equilibrium position. The units for the amplitude can be centimeters or meters, or any convenient unit of distance.

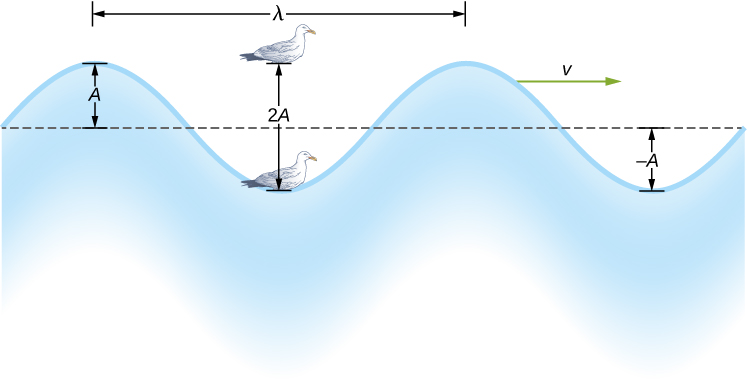
Figure 16.3 An idealized surface water wave passes under a seagull that bobs up and down in simple harmonic motion. The wave has a wavelength [latex] \lambda [/latex], which is the distance between adjacent identical parts of the wave. The amplitude A of the wave is the maximum displacement of the wave from the equilibrium position, which is indicated by the dotted line. In this example, the medium moves up and down, whereas the disturbance of the surface propagates parallel to the surface at a speed v.

The water wave in the figure moves through the medium with a propagation velocity [latex] \overset{\to }{v}. [/latex] The magnitude of the wave velocity is the distance the wave travels in a given time, which is one wavelength in the time of one period, and the wave speed is the magnitude of wave velocity. In equation form, this is

This fundamental relationship holds for all types of waves. For water waves, v is the speed of a surface wave; for sound, v is the speed of sound; and for visible light, v is the speed of light.

Transverse and Longitudinal Waves

We have seen that a simple mechanical wave consists of a periodic disturbance that propagates from one place to another through a medium. In (Figure) (a), the wave propagates in the horizontal direction, whereas the medium is disturbed in the vertical direction. Such a wave is called a transverse wave . In a transverse wave, the wave may propagate in any direction, but the disturbance of the medium is perpendicular to the direction of propagation. In contrast, in a longitudinal wave or compressional wave, the disturbance is parallel to the direction of propagation. (Figure) (b) shows an example of a longitudinal wave. The size of the disturbance is its amplitude A and is completely independent of the speed of propagation v .

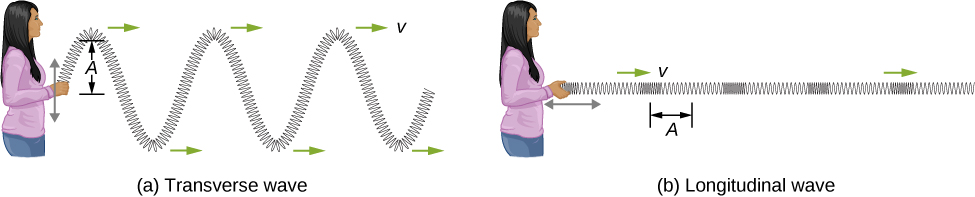
Figure 16.4 (a) In a transverse wave, the medium oscillates perpendicular to the wave velocity. Here, the spring moves vertically up and down, while the wave propagates horizontally to the right. (b) In a longitudinal wave, the medium oscillates parallel to the propagation of the wave. In this case, the spring oscillates back and forth, while the wave propagates to the right.

A simple graphical representation of a section of the spring shown in (Figure) (b) is shown in (Figure) . (Figure) (a) shows the equilibrium position of the spring before any waves move down it. A point on the spring is marked with a blue dot. (Figure) (b) through (g) show snapshots of the spring taken one-quarter of a period apart, sometime after the end of` the spring is oscillated back and forth in the x -direction at a constant frequency. The disturbance of the wave is seen as the compressions and the expansions of the spring. Note that the blue dot oscillates around its equilibrium position a distance A , as the longitudinal wave moves in the positive x -direction with a constant speed. The distance A is the amplitude of the wave. The y -position of the dot does not change as the wave moves through the spring. The wavelength of the wave is measured in part (d). The wavelength depends on the speed of the wave and the frequency of the driving force.

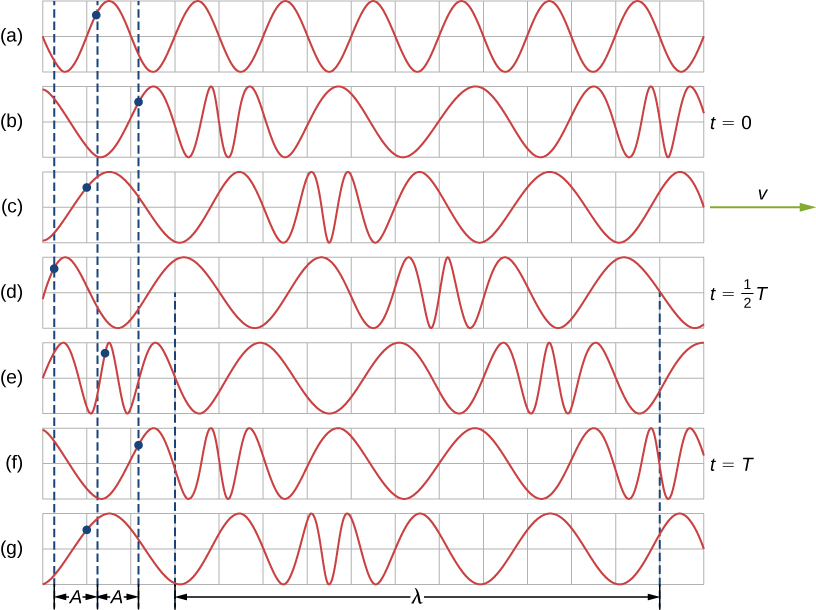
Figure 16.5 (a) This is a simple, graphical representation of a section of the stretched spring shown in (Figure)(b), representing the spring’s equilibrium position before any waves are induced on the spring. A point on the spring is marked by a blue dot. (b–g) Longitudinal waves are created by oscillating the end of the spring (not shown) back and forth along the x-axis. The longitudinal wave, with a wavelength [latex] \lambda [/latex], moves along the spring in the +x-direction with a wave speed v. For convenience, the wavelength is measured in (d). Note that the point on the spring that was marked with the blue dot moves back and forth a distance A from the equilibrium position, oscillating around the equilibrium position of the point.

Waves may be transverse, longitudinal, or a combination of the two. Examples of transverse waves are the waves on stringed instruments or surface waves on water, such as ripples moving on a pond. Sound waves in air and water are longitudinal. With sound waves, the disturbances are periodic variations in pressure that are transmitted in fluids. Fluids do not have appreciable shear strength, and for this reason, the sound waves in them are longitudinal waves. Sound in solids can have both longitudinal and transverse components, such as those in a seismic wave. Earthquakes generate seismic waves under Earth’s surface with both longitudinal and transverse components (called compressional or P-waves and shear or S-waves, respectively). The components of seismic waves have important individual characteristics—they propagate at different speeds, for example. Earthquakes also have surface waves that are similar to surface waves on water. Ocean waves also have both transverse and longitudinal components.

Wave on a String

A student takes a 30.00-m-long string and attaches one end to the wall in the physics lab. The student then holds the free end of the rope, keeping the tension constant in the rope. The student then begins to send waves down the string by moving the end of the string up and down with a frequency of 2.00 Hz. The maximum displacement of the end of the string is 20.00 cm. The first wave hits the lab wall 6.00 s after it was created. (a) What is the speed of the wave? (b) What is the period of the wave? (c) What is the wavelength of the wave?

• The speed of the wave can be derived by dividing the distance traveled by the time.
• The period of the wave is the inverse of the frequency of the driving force.
• The wavelength can be found from the speed and the period [latex] v=\lambda \text{/}T. [/latex]
• The first wave traveled 30.00 m in 6.00 s: [latex] v=\frac{30.00\,\text{m}}{6.00\,\text{s}}=5.00\frac{\text{m}}{\text{s}}. [/latex]
• The period is equal to the inverse of the frequency: [latex] T=\frac{1}{f}=\frac{1}{2.00\,{\text{s}}^{-1}}=0.50\,\text{s}. [/latex]
• The wavelength is equal to the velocity times the period: [latex] \lambda =vT=5.00\frac{\text{m}}{\text{s}}(0.50\,\text{s})=2.50\,\text{m}. [/latex]

Significance

The frequency of the wave produced by an oscillating driving force is equal to the frequency of the driving force.

Check Your Understanding

When a guitar string is plucked, the guitar string oscillates as a result of waves moving through the string. The vibrations of the string cause the air molecules to oscillate, forming sound waves. The frequency of the sound waves is equal to the frequency of the vibrating string. Is the wavelength of the sound wave always equal to the wavelength of the waves on the string?

The wavelength of the waves depends on the frequency and the velocity of the wave. The frequency of the sound wave is equal to the frequency of the wave on the string. The wavelengths of the sound waves and the waves on the string are equal only if the velocities of the waves are the same, which is not always the case. If the speed of the sound wave is different from the speed of the wave on the string, the wavelengths are different. This velocity of sound waves will be discussed in Sound .

Characteristics of a Wave

A transverse mechanical wave propagates in the positive x -direction through a spring (as shown in (Figure) (a)) with a constant wave speed, and the medium oscillates between [latex] \text{+}A [/latex] and [latex] \text{−}A [/latex] around an equilibrium position. The graph in (Figure) shows the height of the spring ( y ) versus the position ( x ), where the x -axis points in the direction of propagation. The figure shows the height of the spring versus the x -position at [latex] t=0.00\,\text{s} [/latex] as a dotted line and the wave at [latex] t=3.00\,\text{s} [/latex] as a solid line. (a) Determine the wavelength and amplitude of the wave. (b) Find the propagation velocity of the wave. (c) Calculate the period and frequency of the wave.

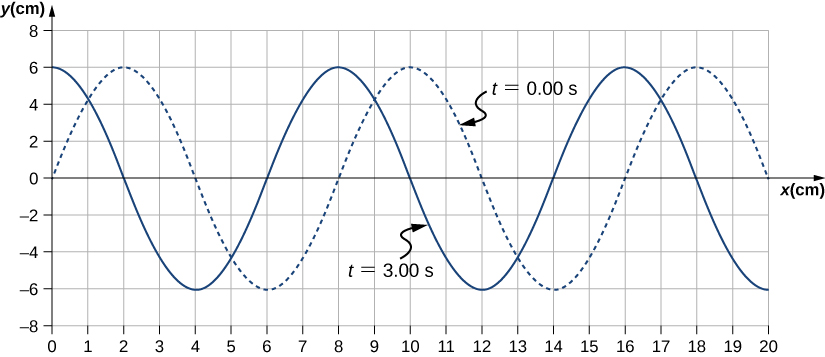
Figure 16.6 A transverse wave shown at two instants of time.

• The amplitude and wavelength can be determined from the graph.
• Since the velocity is constant, the velocity of the wave can be found by dividing the distance traveled by the wave by the time it took the wave to travel the distance.
• The period can be found from [latex] v=\frac{\lambda }{T} [/latex] and the frequency from [latex] f=\frac{1}{T}. [/latex]

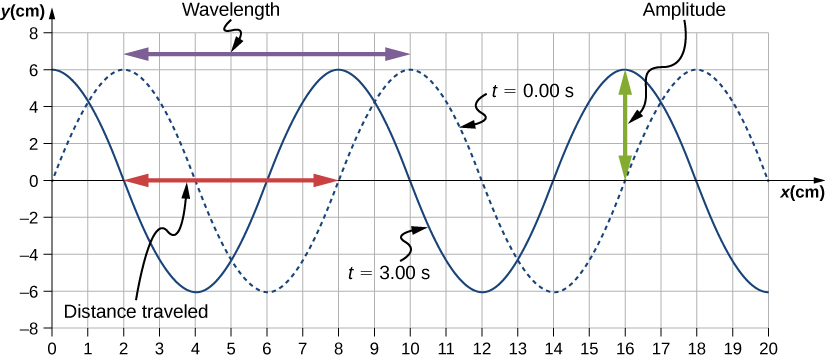
Figure 16.7 Characteristics of the wave marked on a graph of its displacement.

• The distance the wave traveled from time [latex] t=0.00\,\text{s} [/latex] to time [latex] t=3.00\,\text{s} [/latex] can be seen in the graph. Consider the red arrow, which shows the distance the crest has moved in 3 s. The distance is [latex] 8.00\,\text{cm}-2.00\,\text{cm}=6.00\,\text{cm}. [/latex] The velocity is [latex] v=\frac{\text{Δ}x}{\text{Δ}t}=\frac{8.00\,\text{cm}-2.00\,\text{cm}}{3.00\,\text{s}-0.00\,\text{s}}=2.00\,\text{cm/s}. [/latex]
• The period is [latex] T=\frac{\lambda }{v}=\frac{8.00\,\text{cm}}{2.00\,\text{cm/s}}=4.00\,\text{s} [/latex] and the frequency is [latex] f=\frac{1}{T}=\frac{1}{4.00\,\text{s}}=0.25\,\text{Hz}. [/latex]

Note that the wavelength can be found using any two successive identical points that repeat, having the same height and slope. You should choose two points that are most convenient. The displacement can also be found using any convenient point.

The propagation velocity of a transverse or longitudinal mechanical wave may be constant as the wave disturbance moves through the medium. Consider a transverse mechanical wave: Is the velocity of the medium also constant?

• A wave is a disturbance that moves from the point of origin with a wave velocity v .
• A wave has a wavelength [latex] \lambda [/latex], which is the distance between adjacent identical parts of the wave. Wave velocity and wavelength are related to the wave’s frequency and period by [latex] v=\frac{\lambda }{T}=\lambda f. [/latex]
• Mechanical waves are disturbances that move through a medium and are governed by Newton’s laws.
• Electromagnetic waves are disturbances in the electric and magnetic fields, and do not require a medium.
• Matter waves are a central part of quantum mechanics and are associated with protons, electrons, neutrons, and other fundamental particles found in nature.
• A transverse wave has a disturbance perpendicular to the wave’s direction of propagation, whereas a longitudinal wave has a disturbance parallel to its direction of propagation.

Conceptual Questions

Give one example of a transverse wave and one example of a longitudinal wave, being careful to note the relative directions of the disturbance and wave propagation in each.

A sinusoidal transverse wave has a wavelength of 2.80 m. It takes 0.10 s for a portion of the string at a position x to move from a maximum position of [latex] y=0.03\,\text{m} [/latex] to the equilibrium position [latex] y=0. [/latex] What are the period, frequency, and wave speed of the wave?

What is the difference between propagation speed and the frequency of a mechanical wave? Does one or both affect wavelength? If so, how?

Propagation speed is the speed of the wave propagating through the medium. If the wave speed is constant, the speed can be found by [latex] v=\frac{\lambda }{T}=\lambda f. [/latex] The frequency is the number of wave that pass a point per unit time. The wavelength is directly proportional to the wave speed and inversely proportional to the frequency.

Consider a stretched spring, such as a slinky. The stretched spring can support longitudinal waves and transverse waves. How can you produce transverse waves on the spring? How can you produce longitudinal waves on the spring?

Consider a wave produced on a stretched spring by holding one end and shaking it up and down. Does the wavelength depend on the distance you move your hand up and down?

No, the distance you move your hand up and down will determine the amplitude of the wave. The wavelength will depend on the frequency you move your hand up and down, and the speed of the wave through the spring.

A sinusoidal, transverse wave is produced on a stretched spring, having a period T . Each section of the spring moves perpendicular to the direction of propagation of the wave, in simple harmonic motion with an amplitude A . Does each section oscillate with the same period as the wave or a different period? If the amplitude of the transverse wave were doubled but the period stays the same, would your answer be the same?

An electromagnetic wave, such as light, does not require a medium. Can you think of an example that would support this claim?

Storms in the South Pacific can create waves that travel all the way to the California coast, 12,000 km away. How long does it take them to travel this distance if they travel at 15.0 m/s?

Waves on a swimming pool propagate at 0.75 m/s. You splash the water at one end of the pool and observe the wave go to the opposite end, reflect, and return in 30.00 s. How far away is the other end of the pool?

[latex] 2d=vt⇒d=11.25\,\text{m} [/latex]

Wind gusts create ripples on the ocean that have a wavelength of 5.00 cm and propagate at 2.00 m/s. What is their frequency?

How many times a minute does a boat bob up and down on ocean waves that have a wavelength of 40.0 m and a propagation speed of 5.00 m/s?

Scouts at a camp shake the rope bridge they have just crossed and observe the wave crests to be 8.00 m apart. If they shake the bridge twice per second, what is the propagation speed of the waves?

What is the wavelength of the waves you create in a swimming pool if you splash your hand at a rate of 2.00 Hz and the waves propagate at a wave speed of 0.800 m/s?

[latex] v=f\lambda ⇒\lambda =0.400\,\text{m} [/latex]

What is the wavelength of an earthquake that shakes you with a frequency of 10.0 Hz and gets to another city 84.0 km away in 12.0 s?

Radio waves transmitted through empty space at the speed of light [latex] (v=c=3.00\,×\,{10}^{8}\,\text{m/s}) [/latex] by the Voyager spacecraft have a wavelength of 0.120 m. What is their frequency?

Your ear is capable of differentiating sounds that arrive at each ear just 0.34 ms apart, which is useful in determining where low frequency sound is originating from. (a) Suppose a low-frequency sound source is placed to the right of a person, whose ears are approximately 18 cm apart, and the speed of sound generated is 340 m/s. How long is the interval between when the sound arrives at the right ear and the sound arrives at the left ear? (b) Assume the same person was scuba diving and a low-frequency sound source was to the right of the scuba diver. How long is the interval between when the sound arrives at the right ear and the sound arrives at the left ear, if the speed of sound in water is 1500 m/s? (c) What is significant about the time interval of the two situations?

(a) Seismographs measure the arrival times of earthquakes with a precision of 0.100 s. To get the distance to the epicenter of the quake, geologists compare the arrival times of S- and P-waves, which travel at different speeds. If S- and P-waves travel at 4.00 and 7.20 km/s, respectively, in the region considered, how precisely can the distance to the source of the earthquake be determined? (b) Seismic waves from underground detonations of nuclear bombs can be used to locate the test site and detect violations of test bans. Discuss whether your answer to (a) implies a serious limit to such detection. (Note also that the uncertainty is greater if there is an uncertainty in the propagation speeds of the S- and P-waves.)

a. The P-waves outrun the S-waves by a speed of [latex] v=3.20\,\text{km/s;} [/latex] therefore, [latex] \text{Δ}d=0.320\,\text{km}. [/latex] b. Since the uncertainty in the distance is less than a kilometer, our answer to part (a) does not seem to limit the detection of nuclear bomb detonations. However, if the velocities are uncertain, then the uncertainty in the distance would increase and could then make it difficult to identify the source of the seismic waves.

A Girl Scout is taking a 10.00-km hike to earn a merit badge. While on the hike, she sees a cliff some distance away. She wishes to estimate the time required to walk to the cliff. She knows that the speed of sound is approximately 343 meters per second. She yells and finds that the echo returns after approximately 2.00 seconds. If she can hike 1.00 km in 10 minutes, how long would it take her to reach the cliff?

A quality assurance engineer at a frying pan company is asked to qualify a new line of nonstick-coated frying pans. The coating needs to be 1.00 mm thick. One method to test the thickness is for the engineer to pick a percentage of the pans manufactured, strip off the coating, and measure the thickness using a micrometer. This method is a destructive testing method. Instead, the engineer decides that every frying pan will be tested using a nondestructive method. An ultrasonic transducer is used that produces sound waves with a frequency of [latex] f=25\,\text{kHz}. [/latex] The sound waves are sent through the coating and are reflected by the interface between the coating and the metal pan, and the time is recorded. The wavelength of the ultrasonic waves in the coating is 0.076 m. What should be the time recorded if the coating is the correct thickness (1.00 mm)?

• OpenStax University Physics. Authored by : OpenStax CNX. Located at : https://cnx.org/contents/[email protected]:Gofkr9Oy@15 . License : CC BY: Attribution . License Terms : Download for free at http://cnx.org/contents/[email protected]

Privacy Policy

Browse Course Material

Course info.

• Prof. Yen-Jie Lee

Departments

As taught in.

• Atomic, Molecular, Optical Physics
• Classical Mechanics
• Electromagnetism

Learning Resource Types

Physics iii: vibrations and waves, lecture 10: traveling waves.

« Previous | Next »

Lecture Topics

Lecture video: traveling waves.

Prof. Lee introduces the traveling wave solution of the wave equation. He also shows the string “remembers” the shape of the traveling wave though energy stored in the form of kinematic energy.

• Download video
• Download transcript

Lecture Notes

Typed Notes for Lecture 10 (PDF - 1.9MB)

Handwritten Notes for Lecture 10 (PDF - 2.4MB)

Textbook Reading

Chapter 6: Continuum Limit and Fourier Series (PDF - 1.2MB) (section 6.2 to end) 

Chapter 7: Longitudinal Oscillations and Sound (PDF - 1.3MB)  

Chapter 8: Traveling Waves (PDF - 1.4MB) (through section 8.2) 

In-class Demonstrations

You are leaving MIT OpenCourseWare

Traveling Waves

Clickable index:

What is a wave.

Equation of a traveling wave

Motion of the rope

Superposition of waves

The wave equation

Superposition of waves from the wave equation

Reflection of waves

Harmonic waves

Standing waves

If you tie a rope to a pole or wall and pull on it, you can generate tension in the rope.   

If you suddenly move your end of the rope up and down, you’ll find that a disturbance travels down the rope with a velocity v.   We call this a ‘wave’.

The purpose of this last week’s lectures is to study this traveling wave.   We’ll try to understand what determines its velocity, and to understand what happens when it hits the wall.    We’ll restrict our attention to waves in ropes, but in future classes you’ll generalize many of our findings to other types of waves, including sound waves and light waves.    Wave motion is one of the most important topics in physics, and this week we’ll learn about many of their most important qualities.

Not only does this assumption simply our analysis tremendously, but it also happens to be true for many types of waves, including small amplitude waves on strings!

At this point, we don’t really care what that function is.    The shape of the wave is nothing special to us right now.   

Now picture the wave some time t later.    It has moved a distance D x=vt to the right.   We describe it by a height g(x), but we also notice that for any point x, the value of   g(x) is the same as the value of the function f at a point D x to the left.

This means that for the traveling wave, g(x) = f(x-vt).   Hence, f(x-vt) describes the height of the string at some time t later.   This means we can write the height as a function of position and time as:

Example:   At t=0, the height of a wave on a string is described by the function y(x) below, where A is 1 cm, c=1 cm -2 is a constant, and x o is 3 cm (as measured from the hand in the above figures).

If the wave travels towards positive x (away from the hand) with a velocity v=300 cm/s, what is the height of the wave versus x at a time t = 0.1 seconds?

Solution:   The function seems arbitrary, but fortunately we don’t need to know where it comes from to solve the problem!   Use the equation of a traveling wave:

So far, we haven’t said much about exactly how the rope moves when the wave passes by.    A pretty good approximation is that each piece of the rope moves only vertically with no horizontal displacement:

So the height of a piece of rope centered at a position x is then given by y(x,t).   Its velocity and acceleration are in the y direction only since it doesn’t move horizontally, and are given by

Note that in taking the derivatives above, x and v are treated as constants.  

Example:   Say the height of a rope is given at t=0 by

What is its height as a function of time if it travels with a speed 1m/s to the right (positive x), and what is the maximum velocity and acceleration of a point on the rope?

Solution:   The height vs. time is given by the traveling wave equation:

The velocity and acceleration at a point x are given by

The maximum velocity of a piece of rope is (0.033 m/s) and the maximum acceleration is (1.1 m/s 2 ).   Note that the faster the velocity of the wave, the larger the maximum velocity and acceleration are for a piece of the rope.    Also note that the velocity of a piece of rope is not the same as the velocity of the wave, although the two are related.   The figure below illustrates this distinction for a wave whose shape is a sinusoid.   The wave travels to the right and in a time t moves a distant vt.   Notice that the motion of each piece of rope due to the motion of the wave is vertical.   The velocity of individual pieces of the rope is associated with this vertical motion.    It should be clear from the picture that this is not the same as the velocity of the wave, v.

Superposition of Waves

When there are two waves traveling on a string in opposite directions, what happens when they meet?    As it turns out, their heights h 1 and h 2 add to each other:

We’ve used rather unphysical square ‘waves’ in the above illustration to clearly show how when they cross each other, the height of the rope is the sum of their individual heights.    Mathematically, at any instant in time this is expressed as

and at a general time t we can use the relation y(x,t)=f(x-vt) to obtain:

This is called the superposition of waves , and it applies for many types of waves including those along a rope which are the focus of our study.    Simply stated, most waves pass through each other.   As they do, their amplitudes add.   After they cross, they continue along their way with their shapes unaffected.      

The Wave Equation

Recall that for the harmonic oscillator we had an equation

            Consider the motion of a piece of the rope of mass dm and position x (remember that only y changes with time).  

            Newton’s Law says there’s a force if there’s an acceleration.   What is the net force acting on a piece of the rope?   Let’s look at the piece more closely:

There is tension in the rope that acts on both ends of the mass dm.    If the rope is curved, they can combine to produce a net force on the mass.     From the diagram above, it is obvious that the magnitude of this net force is proportional to T and has something to do with the curvature of the rope (and, hence, its second derivative).   

For the piece of rope above, the net force on the rope is obtained by adding the two tension vectors:

The net force is 2T sin q , where q is the angle between the tensions and the horizontal.   Notice that we’ve taken the angle to be the same.    This choice is a convenience and does not affect the generality of our results.

Taking the length of the piece to be very short (dl), we expect the angle to be small and hence the net force is approximately 2T q (we used sin(x)~x for x<<1).

But notice that since the angle is small, q is also approximately equal to tan q (tanx~sinx for x<<1) , which is the magnitude of the slope of each line.    Hence, 2 q is the difference in slope between the two ends of the rope.   

But the difference in slope is just

Solution:  

Superposition of Waves from the Wave Equation

Above, we simply stated that waves add together without giving any justification.   But now that we’ve derived the wave equation from Newton’s Law, we can show that the superposition of waves follows directly from the wave equation and, therefore, from Newton’s Law.      If a wave w 1 travels along a rope, we now know its motion is described by

We could easily imagine the same string with a different wave shape.   This is a wave w 2 with height function f 2 (x-vt):

Such a second wave would have its own function f 2 that satisfies the wave equation.

However, we can put both waves on the same string at the same time.    To show this, we notice that if we add the heights from the two waves to make a new function

then this new function itself satisfies the wave equation:

Hence, we can obtain solutions to the wave equation by adding together individual solutions.   In plain English, if two waves can ride on a rope separately, then they could ride on the rope together if we added their heights together.  

Reflection of Waves

Rope tied to a wall

So far, we haven’t considered what happens when a wave hits a boundary (such as the ceiling in the example above).    Going back to our first example, we see that something must happen because the end of the rope cannot move up and down (it is fixed to a wall).

The condition that the rope is fixed at the wall is known as a boundary condition , and we can express it as y(x W ,t)=0, where x W is the x coordinate of the rope at the wall.    Wave motion must obey this constraint.    To find a solution to wave equation subject to this boundary condition, it is useful to introduce an ‘imaginary’ wave that travels oppositely to the real wave with opposite amplitude (negative displacement).    This is depicted graphically below:

We imagine that the string extends beyond the wall, so that the two waves will collide at x=x W .   The reason for doing this is that when the two waves collide, the piece of rope at x=x W will always remain at y=0.    This enforces our boundary condition.   The figure below illustrates this idea, using the superposition of waves principle.   The solid line indicates the actual position of the rope, which includes both waves added together.   The waves are individually drawn as dashed lines.

The surprising result of this analysis is that after the collision, the ‘imaginary’ wave has passed through to the left of x W and is thus a real wave .   This means that a wave gets reflected from the wall.   It is flipped over (negative amplitude) and travels in the opposite direction with the same speed as the original, incident wave.    Conversely, the incident real wave has passed through the same point and is thus imaginary.    We don’t see it anymore since we only see the actual rope.   

Introducing the imaginary wave is a mathematical trick that allows us to fully solve the wave equation—there is no difference mathematically between using the imaginary rope past the wall and using the wall to hold the rope fixed.    From the wave equation’s point of view, both correspond to the same thing:   the boundary condition that y=0 at the position of the wall.    

Rope tied to a frictionless pole

If instead of being tied to a wall, the rope is tied to a frictionless pole, then the reflection of waves is quite different.   The reason is that the point at the wall is no longer required to stay at y=0.   Instead, the requirement is that there be no vertical force on the rope (imagine that the pole is greasy and therefore frictionless—it cannot exert any force that is not normal to itself).   Since the rope has tension in it, it pulls on the pole with a tension T directed along the rope.    This is shown below.

As a result, the problem of a wave incident on a slippery pole has a different boundary condition: the rope must always be horizontal at the position of the pole.   Mathematically, this means that df/dx=0 at the pole.

To see how this ensures that the derivative is held constant and zero at the pole position, see the illustration below.     A rope is attached to a frictionless pole in the drawing.   Because the rope position is the sum of both waves, it is always horizontal at the position of the pole.

Since the imaginary wave passes through the pole position to become a real wave, it also can be thought of as a reflected wave.    The reflected wave from a frictionless pole is non-inverted and travels in the opposite direction as the real wave.  

Harmonic Waves

There is a special class of wave solutions that is important in physics.   These are known as harmonic waves, because each part of a string undergoes harmonic motion in time.    Why are these important?    It turns out that light is carried by a harmonic wave, as is sound.   Moreover, quantum physics relies exclusively on waves, many of which are harmonic waves.    A knowledge of harmonic waves is therefore very important for your future understanding of these phenomena.   

The height function of a harmonic wave is just a sine wave.   

When we write the function in this form, the wavelength is just l because when x changes from 0 to l , the argument of the sine function goes from 0 to 2 p .    Assuming this is the shape of the wave at a time t=0 and that the wave has a velocity v, then we can write the height at any time as y(x,t) = f(x-vt).  

This gives us

This solution is called a harmonic wave because each piece of the rope undergoes simple harmonic vertical motion with an angular frequency of

Sometimes it is convenient to write the wave height function as

where we have introduced a new constant k known as the wavenumber .    From the definition above one can see that k is given by

Example:   Read Ex. 15-4 in the text (page 450).

Standing Waves

The principle of superposition states that we can add traveling waves together.   What happens when we add two traveling harmonic waves of equal wavelength and amplitude but opposite velocities?  

It’s hard to picture how it turns out, so we’ll resort to a little algebra.   Writing the two waves in the form Asin(kx- w t) and Asin(kx+ w t) (notice the change in sign due to a change in the sign of v and, hence, w ), we obtain:

The picture above plots the height of this wave for different times.   There are x-coordinates where the height of the rope does not move ( nodes ) and x-coordinates where it moves the most ( anti-nodes ).    The anti-nodes are halfway between the nodes, and vice-versa.   The surprising result is that when we add two equal amplitude harmonic waves traveling in opposite directions, we obtain a wave that does not travel at all!!   Instead, it just stands there, oscillating up and down.   For this reason, such a wave is called a standing wave .

You may not recognize it from the above drawings, but a string clamped between two points is basically the same as the string of a musical instrument.    Such strings tend to vibrate, usually with only a single antinode between the fixed points of the string.   This is called the lowest harmonic.   Consider the case of a violin.    The bow excites the string and it vibrates.    The wavelength of the standing wave is fixed by the distance between the bridge of the violin and the neck.  

Since the lowest mode has exactly half a wavelength between the two ends of the string, we can write

where L is the length of the string.    But remember that the frequency is related to the wavelength by:

and the velocity of a wave on a string is given by its tension T and mass density m :

Hence, the frequency of a violin string is given by

Your intuition tells you that you can make the frequency higher by tightening the string (higher tension) or by shortening it (by placing your finger on the string to clamp it in place).   The equation above verifies these ideas.  

• TPC and eLearning
• Read Watch Interact
• What's NEW at TPC?
• Practice Review Test
• Teacher-Tools
• Subscription Selection
• Seat Calculator
• Ad Free Account
• Edit Profile Settings
• Classes (Version 2)
• Student Progress Edit
• Task Properties
• Export Student Progress
• Task, Activities, and Scores
• Metric Conversions Questions
• Metric System Questions
• Metric Estimation Questions
• Significant Digits Questions
• Proportional Reasoning
• Acceleration
• Distance-Displacement
• Dots and Graphs
• Graph That Motion
• Match That Graph
• Name That Motion
• Motion Diagrams
• Pos'n Time Graphs Numerical
• Pos'n Time Graphs Conceptual
• Up And Down - Questions
• Balanced vs. Unbalanced Forces
• Change of State
• Force and Motion
• Mass and Weight
• Match That Free-Body Diagram
• Net Force (and Acceleration) Ranking Tasks
• Newton's Second Law
• Normal Force Card Sort
• Recognizing Forces
• Air Resistance and Skydiving
• Solve It! with Newton's Second Law
• Which One Doesn't Belong?
• Component Addition Questions
• Head-to-Tail Vector Addition
• Projectile Mathematics
• Trajectory - Angle Launched Projectiles
• Trajectory - Horizontally Launched Projectiles
• Vector Addition
• Vector Direction
• Which One Doesn't Belong? Projectile Motion
• Forces in 2-Dimensions
• Being Impulsive About Momentum
• Explosions - Law Breakers
• Hit and Stick Collisions - Law Breakers
• Case Studies: Impulse and Force
• Impulse-Momentum Change Table
• Keeping Track of Momentum - Hit and Stick
• Keeping Track of Momentum - Hit and Bounce
• What's Up (and Down) with KE and PE?
• Energy Conservation Questions
• Energy Dissipation Questions
• Energy Ranking Tasks
• LOL Charts (a.k.a., Energy Bar Charts)
• Match That Bar Chart
• Words and Charts Questions
• Name That Energy
• Stepping Up with PE and KE Questions
• Case Studies - Circular Motion
• Circular Logic
• Forces and Free-Body Diagrams in Circular Motion
• Gravitational Field Strength
• Universal Gravitation
• Angular Position and Displacement
• Linear and Angular Velocity
• Angular Acceleration
• Rotational Inertia
• Balanced vs. Unbalanced Torques
• Getting a Handle on Torque
• Torque-ing About Rotation
• Properties of Matter
• Fluid Pressure
• Buoyant Force
• Sinking, Floating, and Hanging
• Pascal's Principle
• Flow Velocity
• Bernoulli's Principle
• Balloon Interactions
• Charge and Charging
• Charge Interactions
• Charging by Induction
• Conductors and Insulators
• Coulombs Law
• Electric Field
• Electric Field Intensity
• Polarization
• Case Studies: Electric Power
• Know Your Potential
• Light Bulb Anatomy
• I = ∆V/R Equations as a Guide to Thinking
• Parallel Circuits - ∆V = I•R Calculations
• Resistance Ranking Tasks
• Series Circuits - ∆V = I•R Calculations
• Series vs. Parallel Circuits
• Equivalent Resistance
• Period and Frequency of a Pendulum
• Pendulum Motion: Velocity and Force
• Energy of a Pendulum
• Period and Frequency of a Mass on a Spring
• Horizontal Springs: Velocity and Force
• Vertical Springs: Velocity and Force
• Energy of a Mass on a Spring
• Decibel Scale
• Frequency and Period
• Closed-End Air Columns
• Name That Harmonic: Strings
• Rocking the Boat
• Wave Basics
• Matching Pairs: Wave Characteristics
• Wave Interference
• Waves - Case Studies
• Color Addition and Subtraction
• Color Filters
• If This, Then That: Color Subtraction
• Light Intensity
• Color Pigments
• Converging Lenses
• Curved Mirror Images
• Law of Reflection
• Refraction and Lenses
• Total Internal Reflection
• Who Can See Who?
• Formulas and Atom Counting
• Atomic Models
• Bond Polarity
• Entropy Questions
• Cell Voltage Questions
• Heat of Formation Questions
• Reduction Potential Questions
• Oxidation States Questions
• Measuring the Quantity of Heat
• Hess's Law
• Oxidation-Reduction Questions
• Galvanic Cells Questions
• Thermal Stoichiometry
• Molecular Polarity
• Quantum Mechanics
• Balancing Chemical Equations
• Bronsted-Lowry Model of Acids and Bases
• Classification of Matter
• Collision Model of Reaction Rates
• Density Ranking Tasks
• Dissociation Reactions
• Complete Electron Configurations
• Elemental Measures
• Enthalpy Change Questions
• Equilibrium Concept
• Equilibrium Constant Expression
• Equilibrium Calculations - Questions
• Equilibrium ICE Table
• Ionic Bonding
• Lewis Electron Dot Structures
• Limiting Reactants
• Line Spectra Questions
• Mass Stoichiometry
• Measurement and Numbers
• Metals, Nonmetals, and Metalloids
• Metric Estimations
• Metric System
• Molarity Ranking Tasks
• Mole Conversions
• Name That Element
• Names to Formulas
• Names to Formulas 2
• Nuclear Decay
• Particles, Words, and Formulas
• Periodic Trends
• Precipitation Reactions and Net Ionic Equations
• Pressure Concepts
• Pressure-Temperature Gas Law
• Pressure-Volume Gas Law
• Chemical Reaction Types
• Significant Digits and Measurement
• States Of Matter Exercise
• Stoichiometry Law Breakers
• Stoichiometry - Math Relationships
• Subatomic Particles
• Spontaneity and Driving Forces
• Gibbs Free Energy
• Volume-Temperature Gas Law
• Acid-Base Properties
• Energy and Chemical Reactions
• Chemical and Physical Properties
• Valence Shell Electron Pair Repulsion Theory
• Writing Balanced Chemical Equations
• Mission CG1
• Mission CG10
• Mission CG2
• Mission CG3
• Mission CG4
• Mission CG5
• Mission CG6
• Mission CG7
• Mission CG8
• Mission CG9
• Mission EC1
• Mission EC10
• Mission EC11
• Mission EC12
• Mission EC2
• Mission EC3
• Mission EC4
• Mission EC5
• Mission EC6
• Mission EC7
• Mission EC8
• Mission EC9
• Mission RL1
• Mission RL2
• Mission RL3
• Mission RL4
• Mission RL5
• Mission RL6
• Mission KG7
• Mission RL8
• Mission KG9
• Mission RL10
• Mission RL11
• Mission RM1
• Mission RM2
• Mission RM3
• Mission RM4
• Mission RM5
• Mission RM6
• Mission RM8
• Mission RM10
• Mission LC1
• Mission RM11
• Mission LC2
• Mission LC3
• Mission LC4
• Mission LC5
• Mission LC6
• Mission LC8
• Mission SM1
• Mission SM2
• Mission SM3
• Mission SM4
• Mission SM5
• Mission SM6
• Mission SM8
• Mission SM10
• Mission KG10
• Mission SM11
• Mission KG2
• Mission KG3
• Mission KG4
• Mission KG5
• Mission KG6
• Mission KG8
• Mission KG11
• Mission F2D1
• Mission F2D2
• Mission F2D3
• Mission F2D4
• Mission F2D5
• Mission F2D6
• Mission KC1
• Mission KC2
• Mission KC3
• Mission KC4
• Mission KC5
• Mission KC6
• Mission KC7
• Mission KC8
• Mission AAA
• Mission SM9
• Mission LC7
• Mission LC9
• Mission NL1
• Mission NL2
• Mission NL3
• Mission NL4
• Mission NL5
• Mission NL6
• Mission NL7
• Mission NL8
• Mission NL9
• Mission NL10
• Mission NL11
• Mission NL12
• Mission MC1
• Mission MC10
• Mission MC2
• Mission MC3
• Mission MC4
• Mission MC5
• Mission MC6
• Mission MC7
• Mission MC8
• Mission MC9
• Mission RM7
• Mission RM9
• Mission RL7
• Mission RL9
• Mission SM7
• Mission SE1
• Mission SE10
• Mission SE11
• Mission SE12
• Mission SE2
• Mission SE3
• Mission SE4
• Mission SE5
• Mission SE6
• Mission SE7
• Mission SE8
• Mission SE9
• Mission VP1
• Mission VP10
• Mission VP2
• Mission VP3
• Mission VP4
• Mission VP5
• Mission VP6
• Mission VP7
• Mission VP8
• Mission VP9
• Mission WM1
• Mission WM2
• Mission WM3
• Mission WM4
• Mission WM5
• Mission WM6
• Mission WM7
• Mission WM8
• Mission WE1
• Mission WE10
• Mission WE2
• Mission WE3
• Mission WE4
• Mission WE5
• Mission WE6
• Mission WE7
• Mission WE8
• Mission WE9
• Vector Walk Interactive
• Name That Motion Interactive
• Kinematic Graphing 1 Concept Checker
• Kinematic Graphing 2 Concept Checker
• Graph That Motion Interactive
• Two Stage Rocket Interactive
• Rocket Sled Concept Checker
• Force Concept Checker
• Free-Body Diagrams Concept Checker
• Free-Body Diagrams The Sequel Concept Checker
• Skydiving Concept Checker
• Elevator Ride Concept Checker
• Vector Addition Concept Checker
• Vector Walk in Two Dimensions Interactive
• Name That Vector Interactive
• River Boat Simulator Concept Checker
• Projectile Simulator 2 Concept Checker
• Projectile Simulator 3 Concept Checker
• Hit the Target Interactive
• Turd the Target 1 Interactive
• Turd the Target 2 Interactive
• Balance It Interactive
• Go For The Gold Interactive
• Egg Drop Concept Checker
• Fish Catch Concept Checker
• Exploding Carts Concept Checker
• Collision Carts - Inelastic Collisions Concept Checker
• Its All Uphill Concept Checker
• Stopping Distance Concept Checker
• Chart That Motion Interactive
• Roller Coaster Model Concept Checker
• Uniform Circular Motion Concept Checker
• Horizontal Circle Simulation Concept Checker
• Vertical Circle Simulation Concept Checker
• Race Track Concept Checker
• Gravitational Fields Concept Checker
• Orbital Motion Concept Checker
• Angular Acceleration Concept Checker
• Balance Beam Concept Checker
• Torque Balancer Concept Checker
• Aluminum Can Polarization Concept Checker
• Charging Concept Checker
• Name That Charge Simulation
• Coulomb's Law Concept Checker
• Electric Field Lines Concept Checker
• Put the Charge in the Goal Concept Checker
• Circuit Builder Concept Checker (Series Circuits)
• Circuit Builder Concept Checker (Parallel Circuits)
• Circuit Builder Concept Checker (∆V-I-R)
• Circuit Builder Concept Checker (Voltage Drop)
• Equivalent Resistance Interactive
• Pendulum Motion Simulation Concept Checker
• Mass on a Spring Simulation Concept Checker
• Particle Wave Simulation Concept Checker
• Boundary Behavior Simulation Concept Checker
• Slinky Wave Simulator Concept Checker
• Simple Wave Simulator Concept Checker
• Wave Addition Simulation Concept Checker
• Standing Wave Maker Simulation Concept Checker
• Color Addition Concept Checker
• Painting With CMY Concept Checker
• Stage Lighting Concept Checker
• Filtering Away Concept Checker
• InterferencePatterns Concept Checker
• Young's Experiment Interactive
• Plane Mirror Images Interactive
• Who Can See Who Concept Checker
• Optics Bench (Mirrors) Concept Checker
• Name That Image (Mirrors) Interactive
• Refraction Concept Checker
• Total Internal Reflection Concept Checker
• Optics Bench (Lenses) Concept Checker
• Kinematics Preview
• Velocity Time Graphs Preview
• Moving Cart on an Inclined Plane Preview
• Stopping Distance Preview
• Cart, Bricks, and Bands Preview
• Fan Cart Study Preview
• Friction Preview
• Coffee Filter Lab Preview
• Friction, Speed, and Stopping Distance Preview
• Up and Down Preview
• Projectile Range Preview
• Ballistics Preview
• Juggling Preview
• Marshmallow Launcher Preview
• Air Bag Safety Preview
• Colliding Carts Preview
• Collisions Preview
• Engineering Safer Helmets Preview
• Push the Plow Preview
• Its All Uphill Preview
• Energy on an Incline Preview
• Modeling Roller Coasters Preview
• Hot Wheels Stopping Distance Preview
• Ball Bat Collision Preview
• Energy in Fields Preview
• Weightlessness Training Preview
• Roller Coaster Loops Preview
• Universal Gravitation Preview
• Keplers Laws Preview
• Kepler's Third Law Preview
• Charge Interactions Preview
• Sticky Tape Experiments Preview
• Wire Gauge Preview
• Voltage, Current, and Resistance Preview
• Light Bulb Resistance Preview
• Series and Parallel Circuits Preview
• Thermal Equilibrium Preview
• Linear Expansion Preview
• Heating Curves Preview
• Electricity and Magnetism - Part 1 Preview
• Electricity and Magnetism - Part 2 Preview
• Vibrating Mass on a Spring Preview
• Period of a Pendulum Preview
• Wave Speed Preview
• Slinky-Experiments Preview
• Standing Waves in a Rope Preview
• Sound as a Pressure Wave Preview
• DeciBel Scale Preview
• DeciBels, Phons, and Sones Preview
• Sound of Music Preview
• Shedding Light on Light Bulbs Preview
• Models of Light Preview
• Electromagnetic Radiation Preview
• Electromagnetic Spectrum Preview
• EM Wave Communication Preview
• Digitized Data Preview
• Light Intensity Preview
• Concave Mirrors Preview
• Object Image Relations Preview
• Snells Law Preview
• Reflection vs. Transmission Preview
• Magnification Lab Preview
• Reactivity Preview
• Ions and the Periodic Table Preview
• Periodic Trends Preview
• Intermolecular Forces Preview
• Melting Points and Boiling Points Preview
• Reaction Rates Preview
• Ammonia Factory Preview
• Stoichiometry Preview
• Gaining Teacher Access
• Tasks and Classes
• Tasks - Classic
• Subscription
• Subscription Locator
• 1-D Kinematics
• Newton's Laws
• Vectors - Motion and Forces in Two Dimensions
• Momentum and Its Conservation
• Work and Energy
• Circular Motion and Satellite Motion
• Thermal Physics
• Static Electricity
• Electric Circuits
• Vibrations and Waves
• Sound Waves and Music
• Light and Color
• Reflection and Mirrors
• About the Physics Interactives
• Task Tracker
• Usage Policy
• Newtons Laws
• Vectors and Projectiles
• Forces in 2D
• Momentum and Collisions
• Circular and Satellite Motion
• Balance and Rotation
• Electromagnetism
• Waves and Sound
• Forces in Two Dimensions
• Work, Energy, and Power
• Circular Motion and Gravitation
• Sound Waves
• 1-Dimensional Kinematics
• Circular, Satellite, and Rotational Motion
• Einstein's Theory of Special Relativity
• Waves, Sound and Light
• QuickTime Movies
• About the Concept Builders
• Pricing For Schools
• Directions for Version 2
• Measurement and Units
• Relationships and Graphs
• Rotation and Balance
• Vibrational Motion
• Reflection and Refraction
• Teacher Accounts
• Task Tracker Directions
• Kinematic Concepts
• Kinematic Graphing
• Wave Motion
• Sound and Music
• About CalcPad
• 1D Kinematics
• Vectors and Forces in 2D
• Simple Harmonic Motion
• Rotational Kinematics
• Rotation and Torque
• Rotational Dynamics
• Electric Fields, Potential, and Capacitance
• Transient RC Circuits
• Light Waves
• Units and Measurement
• Stoichiometry
• Molarity and Solutions
• Thermal Chemistry
• Acids and Bases
• Kinetics and Equilibrium
• Solution Equilibria
• Oxidation-Reduction
• Nuclear Chemistry
• NGSS Alignments
• 1D-Kinematics
• Projectiles
• Circular Motion
• Magnetism and Electromagnetism
• Graphing Practice
• About the ACT
• ACT Preparation
• For Teachers
• Other Resources
• Newton's Laws of Motion
• Work and Energy Packet
• Static Electricity Review
• Solutions Guide
• Solutions Guide Digital Download
• Motion in One Dimension
• Work, Energy and Power
• Frequently Asked Questions
• Purchasing the Download
• Purchasing the CD
• Purchasing the Digital Download
• About the NGSS Corner
• NGSS Search
• Force and Motion DCIs - High School
• Energy DCIs - High School
• Wave Applications DCIs - High School
• Force and Motion PEs - High School
• Energy PEs - High School
• Wave Applications PEs - High School
• Crosscutting Concepts
• The Practices
• Physics Topics
• NGSS Corner: Activity List
• NGSS Corner: Infographics
• About the Toolkits
• Position-Velocity-Acceleration
• Position-Time Graphs
• Velocity-Time Graphs
• Newton's First Law
• Newton's Second Law
• Newton's Third Law
• Terminal Velocity
• Projectile Motion
• Forces in 2 Dimensions
• Impulse and Momentum Change
• Momentum Conservation
• Work-Energy Fundamentals
• Work-Energy Relationship
• Roller Coaster Physics
• Satellite Motion
• Electric Fields
• Circuit Concepts
• Series Circuits
• Parallel Circuits
• Describing-Waves
• Wave Behavior Toolkit
• Standing Wave Patterns
• Resonating Air Columns
• Wave Model of Light
• Plane Mirrors
• Curved Mirrors
• Teacher Guide
• Using Lab Notebooks
• Current Electricity
• Light Waves and Color
• Reflection and Ray Model of Light
• Refraction and Ray Model of Light
• Classes (Legacy Version)
• Teacher Resources
• Subscriptions

• Newton's Laws
• Einstein's Theory of Special Relativity
• About Concept Checkers
• School Pricing
• Newton's Laws of Motion
• Newton's First Law
• Newton's Third Law

The Anatomy of a Wave

• Anatomy of a Wave
• Energy Transport and the Amplitude of a Wave
• The Speed of a Wave
• The Wave Equation

A transverse wave is a wave in which the particles of the medium are displaced in a direction perpendicular to the direction of energy transport. A transverse wave can be created in a rope if the rope is stretched out horizontally and the end is vibrated back-and-forth in a vertical direction. If a snapshot of such a transverse wave could be taken so as to freeze the shape of the rope in time, then it would look like the following diagram.

The wave shown above can be described by a variety of properties. One such property is amplitude. The amplitude of a wave refers to the maximum amount of displacement of a particle on the medium from its rest position. In a sense, the amplitude is the distance from rest to crest . Similarly, the amplitude can be measured from the rest position to the trough position. In the diagram above, the amplitude could be measured as the distance of a line segment that is perpendicular to the rest position and extends vertically upward from the rest position to point A.

The wavelength is another property of a wave that is portrayed in the diagram above. The wavelength of a wave is simply the length of one complete wave cycle. If you were to trace your finger across the wave in the diagram above, you would notice that your finger repeats its path. A wave is a repeating pattern. It repeats itself in a periodic and regular fashion over both time and space. And the length of one such spatial repetition (known as a wave cycle ) is the wavelength. The wavelength can be measured as the distance from crest to crest or from trough to trough. In fact, the wavelength of a wave can be measured as the distance from a point on a wave to the corresponding point on the next cycle of the wave. In the diagram above, the wavelength is the horizontal distance from A to E, or the horizontal distance from B to F, or the horizontal distance from D to G, or the horizontal distance from E to H. Any one of these distance measurements would suffice in determining the wavelength of this wave.

A longitudinal wave is a wave in which the particles of the medium are displaced in a direction parallel to the direction of energy transport. A longitudinal wave can be created in a slinky if the slinky is stretched out horizontally and the end coil is vibrated back-and-forth in a horizontal direction. If a snapshot of such a longitudinal wave could be taken so as to freeze the shape of the slinky in time, then it would look like the following diagram.

Because the coils of the slinky are vibrating longitudinally, there are regions where they become pressed together and other regions where they are spread apart. A region where the coils are pressed together in a small amount of space is known as a compression. A compression is a point on a medium through which a longitudinal wave is traveling that has the maximum density. A region where the coils are spread apart, thus maximizing the distance between coils, is known as a rarefaction. A rarefaction is a point on a medium through which a longitudinal wave is traveling that has the minimum density. Points A, C and E on the diagram above represent compressions and points B, D, and F represent rarefactions. While a transverse wave has an alternating pattern of crests and troughs, a longitudinal wave has an alternating pattern of compressions and rarefactions.

As discussed above, the wavelength of a wave is the length of one complete cycle of a wave. For a transverse wave, the wavelength is determined by measuring from crest to crest. A longitudinal wave does not have crest; so how can its wavelength be determined? The wavelength can always be determined by measuring the distance between any two corresponding points on adjacent waves. In the case of a longitudinal wave, a wavelength measurement is made by measuring the distance from a compression to the next compression or from a rarefaction to the next rarefaction. On the diagram above, the distance from point A to point C or from point B to point D would be representative of the wavelength.

We Would Like to Suggest ...

Check Your Understanding

Consider the diagram below in order to answer questions #1-2.

1. The wavelength of the wave in the diagram above is given by letter ______.

The wavelength is the distance from crest to crest (or from trough to trough) (or between any two corresponding points on adjacent waves).

2. The amplitude of the wave in the diagram above is given by letter _____.

The amplitude is the distance from rest to crest or from rest to trough.

3. Indicate the interval that represents one full wavelength.

a. A to C b. B to D c. A to G d. C to G

The wavelength is the distance from crest to crest, trough to trough, or from a point on one wave cycle to the corresponding point on the next adjacent wave cycle.

• Boundary Behavior

Talk to our experts

1800-120-456-456

• Travelling Wave

Have you ever sat by a lake and observed the waves created on the surface of the water when you throw a stone into it? This is a good visual example of the propagation of waves and makes it simpler for you to understand travelling of waves and all other concepts related to it. Our universe has an amazing way of informing us about any changes in the physical world. When there are changes the information about that disturbance moves gradually outwards. It moves far from the source of disturbance in all the directions. When the said information travels, it travels in the form of a wave, just like the way waves are created when you throw a stone in the still water. This is known as the travelling wave.

Define Travelling Wave

(image will be uploaded soon)

Before understanding what is travelling wave, let’s understand waves. Wave can be defined as a disturbance in a medium that travels transferring momentum and energy without any actual movement of the medium. However, the medium must have elastic properties. In our everyday life, there are many examples of waves, for example, ocean waves, strings of musical instruments, etc. On the other hand, a travelling wave is a wave in which the positions of minimum and maximum amplitude travel through the medium.

Points To Remember

Here are some of the points that are necessary to keep in mind about the wave:

Every wave has a high point and a low point. The high points are known by the name of crests. On the other hand, the low points are named by troughs.

Amplitude is the maximum distance of the disturbance from the midpoint of the wave to either the top of the crest or the bottom of a trough.

The maximum distance between the two adjacent troughs or the two adjacent crests is known as a wavelength.

Now, the time period is actually the time taken to complete one vibration.

Frequency is the number of vibrations the wave undergoes in one second.

You can witness an inverse relationship between both frequency and time period. The relationship is given below,

The speed of a wave is given by the travelling wave equation,

Where 𝛌 is the wavelength.

What are the Various Types of Travelling Waves?

Each type of wave contains different characteristics. And with these characteristics, we can easily distinguish between them. Here is a list of different types of waves that have been categorized based upon their particle motion.

Pulse Waves - the sudden disturbance that travels through a medium is known as a pulse wave. The disturbance can be caused by a chain reaction or sudden compression of air caused by an explosion. One example of a pulse wave is thunder. It comprises only one crest that travels through the transmission medium.

Continuous Waves - it is an electromagnetic wave that has constant amplitude and frequency. It is a typical sine wave and is considered to be of infinite duration. It was used in the earlier days of radio transmission.

Transverse Waves - in the transverse wave, the movement of the particles is at right angles to the motion of the energy. It is generated through a solid object like a stretched rope. Trampoline is the best example to understand this wave.

Longitudinal Waves - in this type of travelling wave the motion of the wave-particle is in the same direction as the propagation of the wave. In simple words, the movement of the particles is parallel to the motion of the energy. The best example for longitudinal waves is sound waves moving through the air when you hear a loudspeaker playing in the distance.

There is a second way to characterize the waves by types of matter they are able to move or travel through.

Electromagnetic Waves - this type of wave can travel easily through a vacuum. It does not need any medium, soft or hard to travel. An example of an electromagnetic wave is mobile phone waves or sound waves. They don't need any vacuum to travel.

Physical waves - Unlike electromagnetic waves, they require a medium to travel. They are further distinguished on the basis of phases of matter through which they can move.

Longitudinal Waves - these waves can easily pass through liquids and games.

Transverse Waves - they require a solid material or medium to propagate.

Problems based on travelling wave equation

Solved Examples

1: A wave on a rope is shown on the right at some time t.  What is the wavelength of this wave?  If the said frequency is about 4 Hz, what will be the wave speed?

Now, for all the periodic waves, you will find v = λ/T = λf.

Details of the calculation:

The wavelength λ is 3 m. The speed is v = λf = (3 m)(4/s) = 12 m/s.

FAQs on Travelling Wave

1. Do all the Waves have a Defined Wavelength?

Yes, every wave has a specific wavelength, which is defined as the length from one wave crest to the next.

Different kinds of waves have different wavelengths. In water, the surf waves produced by a surfer, have wavelengths of 30–50 m, and the large tsunamis have much longer wavelengths (about 100km). The Sound waves vary in wavelength according to the pitch of it.

2. At What Wavelengths can a Human Hear a Sound?

As per experts and facts, the humans can very well hear sounds possessing wavelengths between 70 mm and 70 m. Any sound above or below this level can not be heard by a human. Example- our universe is filled with cosmic noises. The wavelength of the noise is so high that we cannot hear it on earth.

16.2 Mathematics of Waves

Learning objectives.

By the end of this section, you will be able to:

• Model a wave, moving with a constant wave velocity, with a mathematical expression
• Calculate the velocity and acceleration of the medium
• Show how the velocity of the medium differs from the wave velocity (propagation velocity)

In the previous section, we described periodic waves by their characteristics of wavelength, period, amplitude, and wave speed of the wave. Waves can also be described by the motion of the particles of the medium through which the waves move. The position of particles of the medium can be mathematically modeled as wave function s , which can be used to find the position, velocity, and acceleration of the particles of the medium of the wave at any time.

A pulse can be described as wave consisting of a single disturbance that moves through the medium with a constant amplitude. The pulse moves as a pattern that maintains its shape as it propagates with a constant wave speed. Because the wave speed is constant, the distance the pulse moves in a time Δ t Δ t is equal to Δ x = v Δ t Δ x = v Δ t ( Figure 16.8 ).

Modeling a One-Dimensional Sinusoidal Wave using a Wave Function

Consider a string kept at a constant tension F T F T where one end is fixed and the free end is oscillated between y = + A y = + A and y = − A y = − A by a mechanical device at a constant frequency. Figure 16.9 shows snapshots of the wave at an interval of an eighth of a period, beginning after one period ( t = T ) . ( t = T ) .

Notice that each select point on the string (marked by colored dots) oscillates up and down in simple harmonic motion, between y = + A y = + A and y = − A , y = − A , with a period T . The wave on the string is sinusoidal and is translating in the positive x -direction as time progresses.

At this point, it is useful to recall from your study of algebra that if f ( x ) is some function, then f ( x − d ) f ( x − d ) is the same function translated in the positive x -direction by a distance d . The function f ( x + d ) f ( x + d ) is the same function translated in the negative x -direction by a distance d . We want to define a wave function that will give the y -position of each segment of the string for every position x along the string for every time t .

Looking at the first snapshot in Figure 16.9 , the y -position of the string between x = 0 x = 0 and x = λ x = λ can be modeled as a sine function. This wave propagates down the string one wavelength in one period, as seen in the last snapshot. The wave therefore moves with a constant wave speed of v = λ / T . v = λ / T .

Recall that a sine function is a function of the angle θ θ , oscillating between + 1 + 1 and −1 −1 , and repeating every 2 π 2 π radians ( Figure 16.10 ). However, the y -position of the medium, or the wave function, oscillates between + A + A and − A − A , and repeats every wavelength λ λ .

To construct our model of the wave using a periodic function, consider the ratio of the angle and the position,

Using θ = 2 π λ x θ = 2 π λ x and multiplying the sine function by the amplitude A , we can now model the y -position of the string as a function of the position x :

The wave on the string travels in the positive x -direction with a constant velocity v , and moves a distance vt in a time t . The wave function can now be defined by

It is often convenient to rewrite this wave function in a more compact form. Multiplying through by the ratio 2 π λ 2 π λ leads to the equation

The value 2 π λ 2 π λ is defined as the wave number . The symbol for the wave number is k and has units of inverse meters, m −1 : m −1 :

Recall from Oscillations that the angular frequency is defined as ω ≡ 2 π T . ω ≡ 2 π T . The second term of the wave function becomes

The wave function for a simple harmonic wave on a string reduces to

where A is the amplitude, k = 2 π λ k = 2 π λ is the wave number, ω = 2 π T ω = 2 π T is the angular frequency, the minus sign is for waves moving in the positive x -direction, and the plus sign is for waves moving in the negative x -direction. The velocity of the wave is equal to

Think back to our discussion of a mass on a spring, when the position of the mass was modeled as x ( t ) = A cos ( ω t + ϕ ) . x ( t ) = A cos ( ω t + ϕ ) . The angle ϕ ϕ is a phase shift, added to allow for the fact that the mass may have initial conditions other than x = + A x = + A and v = 0 . v = 0 . For similar reasons, the initial phase is added to the wave function. The wave function modeling a sinusoidal wave, allowing for an initial phase shift ϕ , ϕ , is

is known as the phase of the wave , where ϕ ϕ is the initial phase of the wave function. Whether the temporal term ω t ω t is negative or positive depends on the direction of the wave. First consider the minus sign for a wave with an initial phase equal to zero ( ϕ = 0 ) . ( ϕ = 0 ) . The phase of the wave would be ( k x − ω t ) . ( k x − ω t ) . Consider following a point on a wave, such as a crest. A crest will occur when sin ( k x − ω t ) = 1.00 sin ( k x − ω t ) = 1.00 , that is, when k x − ω t = n π + π 2 , k x − ω t = n π + π 2 , for any integral value of n . For instance, one particular crest occurs at k x − ω t = π 2 . k x − ω t = π 2 . As the wave moves, time increases and x must also increase to keep the phase equal to π 2 . π 2 . Therefore, the minus sign is for a wave moving in the positive x -direction. Using the plus sign, k x + ω t = π 2 . k x + ω t = π 2 . As time increases, x must decrease to keep the phase equal to π 2 . π 2 . The plus sign is used for waves moving in the negative x -direction. In summary, y ( x , t ) = A sin ( k x − ω t + ϕ ) y ( x , t ) = A sin ( k x − ω t + ϕ ) models a wave moving in the positive x -direction and y ( x , t ) = A sin ( k x + ω t + ϕ ) y ( x , t ) = A sin ( k x + ω t + ϕ ) models a wave moving in the negative x -direction.

Equation 16.4 is known as a simple harmonic wave function. A wave function is any function such that f ( x , t ) = f ( x − v t ) . f ( x , t ) = f ( x − v t ) . Later in this chapter, we will see that it is a solution to the linear wave equation. Note that y ( x , t ) = A cos ( k x + ω t + ϕ ′ ) y ( x , t ) = A cos ( k x + ω t + ϕ ′ ) works equally well because it corresponds to a different phase shift ϕ ′ = ϕ − π 2 . ϕ ′ = ϕ − π 2 .

Problem-Solving Strategy

Finding the characteristics of a sinusoidal wave.

• To find the amplitude, wavelength, period, and frequency of a sinusoidal wave, write down the wave function in the form y ( x , t ) = A sin ( k x − ω t + ϕ ) . y ( x , t ) = A sin ( k x − ω t + ϕ ) .
• The amplitude can be read straight from the equation and is equal to A .
• The period of the wave can be derived from the angular frequency ( T = 2 π ω ) . ( T = 2 π ω ) .
• The frequency can be found using f = 1 T . f = 1 T .
• The wavelength can be found using the wave number ( λ = 2 π k ) . ( λ = 2 π k ) .

Example 16.3

Characteristics of a traveling wave on a string.

Find the amplitude, wavelength, period, and speed of the wave.

• The amplitude, wave number, and angular frequency can be read directly from the wave equation: y ( x , t ) = A sin ( k x − ω t ) = 0.2 m sin ( 6.28 m −1 x − 1.57 s −1 t ) . y ( x , t ) = A sin ( k x − ω t ) = 0.2 m sin ( 6.28 m −1 x − 1.57 s −1 t ) . ( A = 0.2 m; k = 6.28 m −1 ; ω = 1.57 s −1 ) ( A = 0.2 m; k = 6.28 m −1 ; ω = 1.57 s −1 )
• The wave number can be used to find the wavelength: k = 2 π λ . λ = 2 π k = 2 π 6.28 m −1 = 1.0 m . k = 2 π λ . λ = 2 π k = 2 π 6.28 m −1 = 1.0 m .
• The period of the wave can be found using the angular frequency: ω = 2 π T . T = 2 π ω = 2 π 1.57 s −1 = 4 s . ω = 2 π T . T = 2 π ω = 2 π 1.57 s −1 = 4 s .
• The speed of the wave can be found using the wave number and the angular frequency. The direction of the wave can be determined by considering the sign of k x ∓ ω t k x ∓ ω t : A negative sign suggests that the wave is moving in the positive x -direction: | v | = ω k = 1.57 s −1 6.28 m −1 = 0.25 m/s . | v | = ω k = 1.57 s −1 6.28 m −1 = 0.25 m/s .

Significance

There is a second velocity to the motion. In this example, the wave is transverse, moving horizontally as the medium oscillates up and down perpendicular to the direction of motion. The graph in Figure 16.12 shows the motion of the medium at point x = 0.60 m x = 0.60 m as a function of time. Notice that the medium of the wave oscillates up and down between y = + 0.20 m y = + 0.20 m and y = −0.20 m y = −0.20 m every period of 4.0 seconds.

Check Your Understanding 16.3

The wave function above is derived using a sine function. Can a cosine function be used instead?

Velocity and Acceleration of the Medium

As seen in Example 16.4 , the wave speed is constant and represents the speed of the wave as it propagates through the medium, not the speed of the particles that make up the medium. The particles of the medium oscillate around an equilibrium position as the wave propagates through the medium. In the case of the transverse wave propagating in the x -direction, the particles oscillate up and down in the y -direction, perpendicular to the motion of the wave. The velocity of the particles of the medium is not constant, which means there is an acceleration. The velocity of the medium, which is perpendicular to the wave velocity in a transverse wave, can be found by taking the partial derivative of the position equation with respect to time. The partial derivative is found by taking the derivative of the function, treating all variables as constants, except for the variable in question. In the case of the partial derivative with respect to time t , the position x is treated as a constant. Although this may sound strange if you haven’t seen it before, the object of this exercise is to find the transverse velocity at a point, so in this sense, the x -position is not changing. We have

The magnitude of the maximum velocity of the medium is | v y max | = A ω | v y max | = A ω . This may look familiar from the Oscillations and a mass on a spring.

We can find the acceleration of the medium by taking the partial derivative of the velocity equation with respect to time,

The magnitude of the maximum acceleration is | a y max | = A ω 2 . | a y max | = A ω 2 . The particles of the medium, or the mass elements, oscillate in simple harmonic motion for a mechanical wave.

The Linear Wave Equation

We have just determined the velocity of the medium at a position x by taking the partial derivative, with respect to time, of the position y . For a transverse wave, this velocity is perpendicular to the direction of propagation of the wave. We found the acceleration by taking the partial derivative, with respect to time, of the velocity, which is the second time derivative of the position:

Now consider the partial derivatives with respect to the other variable, the position x , holding the time constant. The first derivative is the slope of the wave at a point x at a time t ,

The second partial derivative expresses how the slope of the wave changes with respect to position—in other words, the curvature of the wave, where

The ratio of the acceleration and the curvature leads to a very important relationship in physics known as the linear wave equation . Taking the ratio and using the equation v = ω / k v = ω / k yields the linear wave equation (also known simply as the wave equation or the equation of a vibrating string),

Equation 16.6 is the linear wave equation, which is one of the most important equations in physics and engineering. We derived it here for a transverse wave, but it is equally important when investigating longitudinal waves. This relationship was also derived using a sinusoidal wave, but it successfully describes any wave or pulse that has the form y ( x , t ) = f ( x ∓ v t ) . y ( x , t ) = f ( x ∓ v t ) . These waves result due to a linear restoring force of the medium—thus, the name linear wave equation. Any wave function that satisfies this equation is a linear wave function.

An interesting aspect of the linear wave equation is that if two wave functions are individually solutions to the linear wave equation, then the sum of the two linear wave functions is also a solution to the wave equation. Consider two transverse waves that propagate along the x -axis, occupying the same medium. Assume that the individual waves can be modeled with the wave functions y 1 ( x , t ) = f ( x ∓ v t ) y 1 ( x , t ) = f ( x ∓ v t ) and y 2 ( x , t ) = g ( x ∓ v t ) , y 2 ( x , t ) = g ( x ∓ v t ) , which are solutions to the linear wave equations and are therefore linear wave functions. The sum of the wave functions is the wave function

Consider the linear wave equation:

This has shown that if two linear wave functions are added algebraically, the resulting wave function is also linear. This wave function models the displacement of the medium of the resulting wave at each position along the x -axis. If two linear waves occupy the same medium, they are said to interfere. If these waves can be modeled with a linear wave function, these wave functions add to form the wave equation of the wave resulting from the interference of the individual waves. The displacement of the medium at every point of the resulting wave is the algebraic sum of the displacements due to the individual waves.

Taking this analysis a step further, if wave functions y 1 ( x , t ) = f ( x ∓ v t ) y 1 ( x , t ) = f ( x ∓ v t ) and y 2 ( x , t ) = g ( x ∓ v t ) y 2 ( x , t ) = g ( x ∓ v t ) are solutions to the linear wave equation, then A y 1 ( x , t ) + B y 2 ( x , t ) , A y 1 ( x , t ) + B y 2 ( x , t ) , where A and B are constants, is also a solution to the linear wave equation. This property is known as the principle of superposition. Interference and superposition are covered in more detail in Interference of Waves .

Example 16.4

Interference of waves on a string.

• Write the wave function of the second wave: y 2 ( x , t ) = A sin ( 2 k x + 2 ω t ) . y 2 ( x , t ) = A sin ( 2 k x + 2 ω t ) .
• Write the resulting wave function: y R ( x , t ) = y 1 ( x , t ) + y ( x , t ) = A sin ( k x − ω t ) + A sin ( 2 k x + 2 ω t ) . y R ( x , t ) = y 1 ( x , t ) + y ( x , t ) = A sin ( k x − ω t ) + A sin ( 2 k x + 2 ω t ) .
• Find the partial derivatives: ∂ y R ( x , t ) ∂ x = + A k cos ( k x − ω t ) + 2 A k cos ( 2 k x + 2 ω t ) , ∂ 2 y R ( x , t ) ∂ x 2 = − A k 2 sin ( k x − ω t ) − 4 A k 2 sin ( 2 k x + 2 ω t ) , ∂ y R ( x , t ) ∂ t = − A ω cos ( k x − ω t ) + 2 A ω cos ( 2 k x + 2 ω t ) , ∂ 2 y R ( x , t ) ∂ t 2 = − A ω 2 sin ( k x − ω t ) − 4 A ω 2 sin ( 2 k x + 2 ω t ) . ∂ y R ( x , t ) ∂ x = + A k cos ( k x − ω t ) + 2 A k cos ( 2 k x + 2 ω t ) , ∂ 2 y R ( x , t ) ∂ x 2 = − A k 2 sin ( k x − ω t ) − 4 A k 2 sin ( 2 k x + 2 ω t ) , ∂ y R ( x , t ) ∂ t = − A ω cos ( k x − ω t ) + 2 A ω cos ( 2 k x + 2 ω t ) , ∂ 2 y R ( x , t ) ∂ t 2 = − A ω 2 sin ( k x − ω t ) − 4 A ω 2 sin ( 2 k x + 2 ω t ) .

∂ 2 y ( x , t ) ∂ x 2 = 1 v 2 ∂ 2 y ( x , t ) ∂ t 2 , − A k 2 sin ( k x − ω t ) − 4 A k 2 sin ( 2 k x + 2 ω t ) = 1 v 2 ( − A ω 2 sin ( k x − ω t ) − 4 A ω 2 sin ( 2 k x + 2 ω t ) ) , k 2 ( − A sin ( k x − ω t ) − 4 A sin ( 2 k x + 2 ω t ) ) = ω 2 v 2 ( − A sin ( k x − ω t ) − 4 A sin ( 2 k x + 2 ω t ) ) , k 2 = ω 2 v 2 , | v | = ω k . ∂ 2 y ( x , t ) ∂ x 2 = 1 v 2 ∂ 2 y ( x , t ) ∂ t 2 , − A k 2 sin ( k x − ω t ) − 4 A k 2 sin ( 2 k x + 2 ω t ) = 1 v 2 ( − A ω 2 sin ( k x − ω t ) − 4 A ω 2 sin ( 2 k x + 2 ω t ) ) , k 2 ( − A sin ( k x − ω t ) − 4 A sin ( 2 k x + 2 ω t ) ) = ω 2 v 2 ( − A sin ( k x − ω t ) − 4 A sin ( 2 k x + 2 ω t ) ) , k 2 = ω 2 v 2 , | v | = ω k .

Check Your Understanding 16.4

The wave equation ∂ 2 y ( x , t ) ∂ x 2 = 1 v 2 ∂ 2 y ( x , t ) ∂ t 2 ∂ 2 y ( x , t ) ∂ x 2 = 1 v 2 ∂ 2 y ( x , t ) ∂ t 2 works for any wave of the form y ( x , t ) = f ( x ∓ v t ) . y ( x , t ) = f ( x ∓ v t ) . In the previous section, we stated that a cosine function could also be used to model a simple harmonic mechanical wave. Check if the wave

is a solution to the wave equation.

Any disturbance that complies with the wave equation can propagate as a wave moving along the x -axis with a wave speed v . It works equally well for waves on a string, sound waves, and electromagnetic waves. This equation is extremely useful. For example, it can be used to show that electromagnetic waves move at the speed of light.

As an Amazon Associate we earn from qualifying purchases.

This book may not be used in the training of large language models or otherwise be ingested into large language models or generative AI offerings without OpenStax's permission.

Want to cite, share, or modify this book? This book uses the Creative Commons Attribution License and you must attribute OpenStax.

Access for free at https://openstax.org/books/university-physics-volume-1/pages/1-introduction

• Authors: William Moebs, Samuel J. Ling, Jeff Sanny
• Publisher/website: OpenStax
• Book title: University Physics Volume 1
• Publication date: Sep 19, 2016
• Location: Houston, Texas
• Book URL: https://openstax.org/books/university-physics-volume-1/pages/1-introduction
• Section URL: https://openstax.org/books/university-physics-volume-1/pages/16-2-mathematics-of-waves

© Jan 19, 2024 OpenStax. Textbook content produced by OpenStax is licensed under a Creative Commons Attribution License . The OpenStax name, OpenStax logo, OpenStax book covers, OpenStax CNX name, and OpenStax CNX logo are not subject to the Creative Commons license and may not be reproduced without the prior and express written consent of Rice University.

• Collections

• APS Journals

Ocean Measurements Detect Conditions for Giant Waves

Researchers still disagree on what causes rare and large “rogue waves,” which can damage ships, lighthouses, and other structures. Now, using combined measurements of wave heights and wind speed in an oceanic region known for its rough seas, a research team has demonstrated that wind can produce the wave conditions expected to lead to rogue waves [ 1 ]. Previously, this idea was demonstrated only in laboratory experiments. The researchers hope this new understanding will contribute to the development of methods for predicting this dangerous phenomenon.

There is no consensus on what causes rogue waves in the ocean, says Alessandro Toffoli, an expert in infrastructure engineering at the University of Melbourne, Australia. One prominent view is that oceanic rogue waves occur purely through a statistical effect: although waves typically follow a “normal,” or Gaussian, distribution, with heights strongly clustering around an average, a fortuitous convergence of many such waves can occasionally produce a very large wave.

In contrast, laboratory experiments and theoretical models suggest that, under the right conditions, nonlinear ocean dynamics can amplify waves, making the distribution of wave heights depart from a Gaussian. The distribution can spread out, giving large waves higher probabilities than in a Gaussian distribution. Unfortunately, says Toffoli, no study has yet observed such increased numbers of larger waves in the ocean. “So this idea has mostly been dismissed as unrealistic,” he says. “Are there rogue sea states where rogue waves thrive? The answer to this remains elusive.”

To look for such states, Toffoli and colleagues undertook an expedition in the Southern Ocean, a region around Antarctica known for strong winds and large waves. The team made measurements from a South African icebreaker in the austral winter, in June and July 2017. During the voyage, the researchers used a stereo pair of cameras to map the water surface height and measure the statistical characteristics of the waves viewed off one side of the ship. Alongside these measurements, they collected data on local atmospheric conditions, including wind speed.

Toffoli says that the wind data allowed the team to study how wave characteristics change as waves are driven by the wind. Assuming a relatively steady wind, waves start out moving slowly with shorter wavelengths and gradually move faster as their wavelengths increase. So the team could use the ratio of the wave speed to the wind speed as a proxy for wave age. As the team’s analysis showed, younger waves behave very differently than older waves.

In seas with relatively young waves, the wave heights were about 3.5–4.5 m, and they were particularly steep, meaning they had a high ratio of height to wavelength. Seas in this young stage—with waves moving at about half the wind speed and deriving energy from it—also showed frequent white caps, caused by steep waves breaking. In contrast, seas with older waves—their speeds now as high as the prevailing wind or even higher—were about 2–3 m high, less steep, and lacked white caps.

The team estimated the kurtosis, a statistical measure of the wave size distribution’s departure from a Gaussian. The higher the kurtosis, the more likely are extra-large waves, including rogue waves. In the wind-driven young seas, with slow, strongly driven waves, the researchers found a kurtosis of 3.4, well above the 3.0 value characteristic of seas with a Gaussian distribution of waves. In older seas, the distribution returned to a Gaussian. This observation suggests that the action of strong winds during early stages of wave growth can stir nonlinear ocean dynamics, leading to a strongly non-Gaussian distribution of waves and more frequent rogue waves.

“Until now,” says Toffoli, “this has only been observed in controlled laboratory experiments where waves were mechanically generated.” In future work, Toffoli and colleagues hope to characterize rogue seas more accurately. “We need to acquire more data to consolidate our finding,” he says. The team also aims to clarify the physical mechanisms behind rogue waves with the eventual goal of developing ways to forecast their occurrence.

“This is an important contribution to physics and engineering science,” says Amin Chabchoub, a physical oceanographer and expert on extreme waves at the University of Kyoto, Japan. “The key contribution is to provide evidence for a mechanism operating in the Southern Ocean that increases the frequency of extreme wave events in the presence of wind.” He expects the results to lead to improved shipbuilding standards and to help in the prediction of rogue waves.

–Mark Buchanan

Mark Buchanan is a freelance science writer who splits his time between Abergavenny, UK, and Notre Dame de Courson, France.

• A. Toffoli et al. , “Observations of rogue seas in the Southern Ocean,” Phys. Rev. Lett. 132 , 154101 (2024) .

More Information

Focus: Making Rogue Waves with Wind and Water (describes earlier work by Toffoli et al. )

Viewpoint: A Unifying Framework for Describing Rogue Waves (co-written by Chabchoub)

Observations of Rogue Seas in the Southern Ocean

A. Toffoli, A. Alberello, H. Clarke, F. Nelli, A. Benetazzo, F. Bergamasco, B. Ntamba Ntamba, M. Vichi, and M. Onorato

Phys. Rev. Lett. 132 , 154101 (2024)

Published April 12, 2024

Subject Areas

Related articles.

A Supernova Remnant Shaped by Vortices

The clumpy structure of a ring of gas ejected by the progenitor star of the supernova 1987A could have formed when vortices in the gas interacted. Read More »

Prizes for Videos Featuring Mickey Mouse and Laptop Cables

The winners of the third annual “Gallery of Soft Matter” competition included posters portraying robotic leaves and cannibalizing droplets and a video with what might be Steamboat Willie’s first appearance at the APS March Meeting. Read More »

Rainproof Water Striders

Researchers reveal how water striders survive collisions with raindrops that are much larger than the insects—a result that could help in understanding how microplastics are transported in water. Read More »

Sign up to receive weekly email alerts from Physics Magazine .

• Skip to main content
• Keyboard shortcuts for audio player

• LISTEN & FOLLOW
• Apple Podcasts
• Google Podcasts
• Amazon Music
• Amazon Alexa

Your support helps make our show possible and unlocks access to our sponsor-free feed.

How climate change and physics affect baseball, America's favorite pastime

Regina G. Barber

Berly McCoy

Rachel Carlson

Rebecca Ramirez

Yu Darvish #11 of the San Diego Padres throws a pitch during the third inning against the St. Louis Cardinals at Petco Park on April 2, 2024 in San Diego, California. Brandon Sloter/Getty Images hide caption

Yu Darvish #11 of the San Diego Padres throws a pitch during the third inning against the St. Louis Cardinals at Petco Park on April 2, 2024 in San Diego, California.

It's baseball season! And when we here at Short Wave think of baseball, we naturally think of physics. To get the inside scoop on the physics of baseball, like how to hit a home run, we talk to Frederic Bertley, CEO and President of the Center of Science and Industry, a science museum in Columbus, Ohio. He also talks to host Regina G. Barber about how climate change is affecting the game.

Interested in the science of other sports? Email us at [email protected] — we'd love to hear from you.

Listen to Short Wave on Spotify , Apple Podcasts and Google Podcasts .

Listen to every episode of Short Wave sponsor-free and support our work at NPR by signing up for Short Wave+ at plus.npr.org/shortwave .

This episode was produced by Berly McCoy and Rachel Carlson. It was edited and fact-checked by Rebecca Ramirez. Patrick Murray was the audio engineer.

• climate change

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons
• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

• Last updated
• Save as PDF
• Page ID 17096

learning objectives

• Describe process of energy and mass transfer during wave motion

Vibrations and waves are extremely important phenomena in physics. In nature, oscillations are found everywhere. From the jiggling of atoms to the large oscillations of sea waves, we find examples of vibrations in almost every physical system. In physics a wave can be thought of as a disturbance or oscillation that travels through space-time, accompanied by a transfer of energy. Wave motion transfers energy from one point to another, often with no permanent displacement of the particles of the medium —that is, with little or no associated mass transport. They consist, instead, of oscillations or vibrations around almost fixed locations.

The emphasis of the last point highlights an important misconception of waves. Waves transfer energy not mass. An easy way to see this is to imagine a floating ball a few yards out to sea. As the waves propagate (i.e., travel) towards the shore, the ball will not come towards the shore. It may come to shore eventually due to the tides, current or wind, but the waves themselves will not carry the ball with them. A wave only moves mass perpendicular to the direction of propagation—in this case up and down, as illustrated in the figure below:

Wave motion : The point along the axis is analogous to the floating ball at sea. We notice that while it moves up and down it does not move in the direction of the wave’s propagation.

A wave can be transverse or longitudinal depending on the direction of its oscillation. Transverse waves occur when a disturbance causes oscillations perpendicular (at right angles) to the propagation (the direction of energy transfer). Longitudinal waves occur when the oscillations are parallel to the direction of propagation. While mechanical waves can be both transverse and longitudinal, all electromagnetic waves are transverse. Sound, for example, is a longitudinal wave.

The description of waves is closely related to their physical origin for each specific instance of a wave process. For example, acoustics is distinguished from optics in that sound waves are related to a mechanical rather than an electromagnetic (light) wave transfer caused by vibration. Therefore, concepts such as mass, momentum, inertia or elasticity become crucial in describing acoustic (as distinct from optic) wave processes. This difference in origin introduces certain wave characteristics particular to the properties of the medium involved. In this chapter we will closely examine the difference between longitudinal and transverse waves along with some of the properties they possess. We will also learn how waves are fundamental in describing motion of many applicable physical systems.

The Wave Equation : A brief introduction to the wave equation, discussing wave velocity, frequency, wavelength, and period.

Transverse Waves

Transverse waves propagate through media with a speed →vwv→w orthogonally to the direction of energy transfer.

• Describe properties of the transverse wave

A transverse wave is a moving wave that consists of oscillations occurring perpendicular (or right angled) to the direction of energy transfer. If a transverse wave is moving in the positive x -direction, its oscillations are in up and down directions that lie in the y–z plane. Light is an example of a transverse wave. For transverse waves in matter, the displacement of the medium is perpendicular to the direction of propagation of the wave. A ripple on a pond and a wave on a string are easily visualized transverse waves.

Transverse waves are waves that are oscillating perpendicularly to the direction of propagation. If you anchor one end of a ribbon or string and hold the other end in your hand, you can create transverse waves by moving your hand up and down. Notice though, that you can also launch waves by moving your hand side-to-side. This is an important point. There are two independent directions in which wave motion can occur. In this case, these are the y and z directions mentioned above. depicts the motion of a transverse wave. Here we observe that the wave is moving in t and oscillating in the x-y plane. A wave can be thought as comprising many particles (as seen in the figure) which oscillate up and down. In the figure we observe this motion to be in x-y plane (denoted by the red line in the figure). As time passes the oscillations are separated by units of time. The result of this separation is the sine curve we expect when we plot position versus time.

Sine Wave : The direction of propagation of this wave is along the t axis.

When a wave travels through a medium–i.e., air, water, etc., or the standard reference medium (vacuum)–it does so at a given speed: this is called the speed of propagation. The speed at which the wave propagates is denoted and can be found using the following formula:

\[\mathrm{v=fλ}\]

where v is the speed of the wave, f is the frequency , and is the wavelength. The wavelength spans crest to crest while the amplitude is 1/2 the total distance from crest to trough. Transverse waves have their applications in many areas of physics. Examples of transverse waves include seismic S (secondary) waves, and the motion of the electric (E) and magnetic (M) fields in an electromagnetic plane waves, which both oscillate perpendicularly to each other as well as to the direction of energy transfer. Therefore an electromagnetic wave consists of two transverse waves, visible light being an example of an electromagnetic wave.

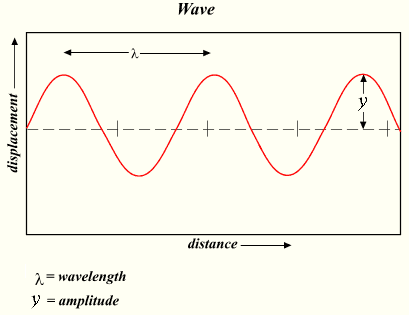
Wavelength and Amplitude : The wavelength is the distance between adjacent crests. The amplitude is the 1/2 the distance from crest to trough.

Two Types of Waves: Longitudinal vs. Transverse : Even ocean waves!

Longitudinal Waves

Longitudinal waves, sometimes called compression waves, oscillate in the direction of propagation.

• Give properties and provide examples of the longitudinal wave

Longitudinal waves have the same direction of vibration as their direction of travel. This means that the movement of the medium is in the same direction as the motion of the wave. Some longitudinal waves are also called compressional waves or compression waves. An easy experiment for observing longitudinal waves involves taking a Slinky and holding both ends. After compressing and releasing one end of the Slinky (while still holding onto the end), a pulse of more concentrated coils will travel to the end of the Slinky.

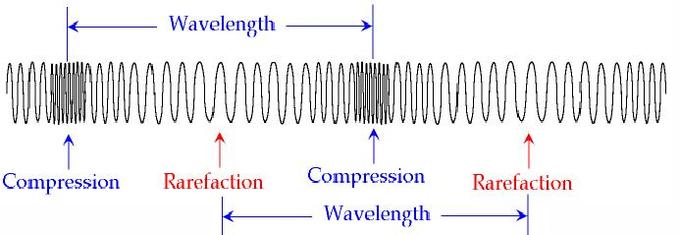
Longitudinal Waves : A compressed Slinky is an example of a longitudinal wave. The wve propagates in the same direction of oscillation.

Like transverse waves, longitudinal waves do not displace mass. The difference is that each particle which makes up the medium through which a longitudinal wave propagates oscillates along the axis of propagation. In the example of the Slinky, each coil will oscillate at a point but will not travel the length of the Slinky. It is important to remember that energy, in this case in the form of a pulse, is being transmitted and not the displaced mass.

Longitudinal waves can sometimes also be conceptualized as pressure waves. The most common pressure wave is the sound wave. Sound waves are created by the compression of a medium, usually air. Longitudinal sound waves are waves of alternating pressure deviations from the equilibrium pressure, causing local regions of compression and rarefaction. Matter in the medium is periodically displaced by a sound wave, and thus oscillates. When people make a sound, whether it is through speaking or hitting something, they are compressing the air particles to some significant amount. By doing so, they create transverse waves. When people hear sounds, their ears are sensitive to the pressure differences and interpret the waves as different tones.

Water Waves

Water waves can be commonly observed in daily life, and comprise both transverse and longitudinal wave motion.

• Describe particle movement in water waves

Water waves, which can be commonly observed in our daily lives, are of specific interest to physicists. Describing detailed fluid dynamics in water waves is beyond the scope of introductory physics courses. Although we often observe water wave propagating in 2D, in this atom we will limit our discussion to 1D propagation.

Water waves : Surface waves in water

The uniqueness of water waves is found in the observation that they comprise both transverse and longitudinal wave motion. As a result, the particles composing the wave move in clockwise circular motion, as seen in. Oscillatory motion is highest at the surface and diminishes exponentially with depth. Waves are generated by wind passing over the surface of the sea. As long as the waves propagate slower than the wind speed just above the waves, there is an energy transfer from the wind to the waves. Both air pressure differences between the upwind and the lee side of a wave crest, as well as friction on the water surface by the wind (making the water to go into the shear stress), contribute to the growth of the waves.

In the case of monochromatic linear plane waves in deep water, particles near the surface move in circular paths, creating a combination of longitudinal (back and forth) and transverse (up and down) wave motions. When waves propagate in shallow water (where the depth is less than half the wavelength ), the particle trajectories are compressed into ellipses. As the wave amplitude (height) increases, the particle paths no longer form closed orbits; rather, after the passage of each crest, particles are displaced slightly from their previous positions, a phenomenon known as Stokes drift.

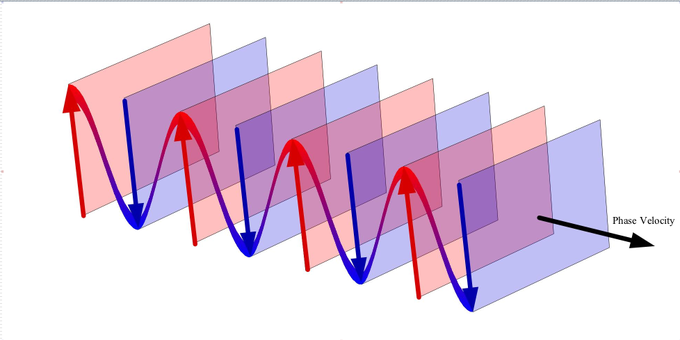
Plane wave : We see a wave propagating in the direction of the phase velocity. The wave can be thought to be made up of planes orthogonal to the direction of the phase velocity.

Since water waves transport energy, attempts to generate power from them have been made by utilizing the physical motion of such waves. Although larger waves are more powerful, wave power is also determined by wave speed, wavelength, and water density. Deep water corresponds with a water depth larger than half the wavelength, as is a common case in the sea and ocean. In deep water, longer-period waves propagate faster and transport their energy faster. The deep-water group velocity is half the phase velocity. In shallow water for wavelengths larger than about twenty times the water depth (as often found near the coast), the group velocity is equal to the phase velocity. These methods have proven viable in some cases but do not provide a fully sustainable form of renewable energy to date.

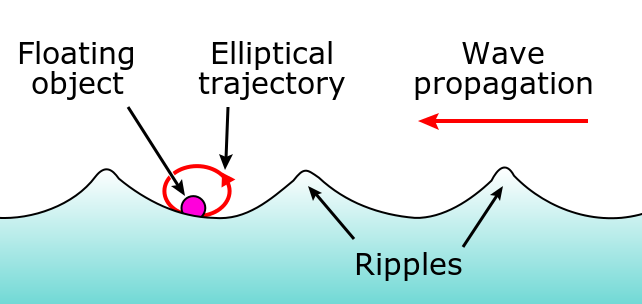
Water waves : The motion water waves causes particles to follow clockwise circular motion. This is a result of the wave having both transverse and longitudinal properties.

Wavelength, Freqency in Relation to Speed

Waves are defined by its frequency, wavelength, and amplitude among others. They also have two kinds of velocity: phase and group velocity.

• Identify major characteristic properties of waves

Characteristics of Waves

Waves have certain characteristic properties which are observable at first notice. The first property to note is the amplitude. The amplitude is half of the distance measured from crest to trough. We also observe the wavelength, which is the spatial period of the wave (e.g. from crest to crest or trough to trough). We denote the wavelength by the Greek letter λλ.

The frequency of a wave is the number of cycles per unit time — one can think of it as the number of crests which pass a fixed point per unit time. Mathematically, we make the observation that,

Frequencies of different sine waves. : The red wave has a low frequency sine there is very little repetition of cycles. Conversely we say that the purple wave has a high frequency. Note that time increases along the horizontal.

\[\mathrm{f=\dfrac{1}{T}}\]

where T is the period of oscillation. Frequency and wavelength can also be related-* with respects to a “speed” of a wave. In fact,

\[\mathrm{v=fλ}]

where v is called the wave speed, or more commonly,the phase velocity, the rate at which the phase of the wave propagates in space. This is the velocity at which the phase of any one frequency component of the wave travels. For such a component, any given phase of the wave (for example, the crest) will appear to travel at the phase velocity.

Finally, the group velocity of a wave is the velocity with which the overall shape of the waves’ amplitudes — known as the modulation or envelope of the wave — propagates through space. In, one may see that the overall shape (or “envelope”) propagates to the right, while the phase velocity is negative.

Fig 2 : This shows a wave with the group velocity and phase velocity going in different directions. (The group velocity is positive and the phase velocity is negative. )

Energy Transportation

Waves transfer energy which can be used to do work.

• Relate direction of energy and wave transportation

Energy transportion is essential to waves. It is a common misconception that waves move mass. Waves carry energy along an axis defined to be the direction of propagation. One easy example is to imagine that you are standing in the surf and you are hit by a significantly large wave, and once you are hit you are displaced (unless you hold firmly to your ground!). In this sense the wave has done work (it applied a force over a distance). Since work is done over time, the energy carried by a wave can be used to generate power.

Water Wave : Waves that are more massive or have a greater velocity transport more energy.

Similarly we find that electromagnetic waves carry energy. Electromagnetic radiation (EMR) carries energy—sometimes called radiant energy—through space continuously away from the source (this is not true of the near-field part of the EM field). Electromagnetic waves can be imagined as a self-propagating transverse oscillating wave of electric and magnetic fields. EMR also carries both momentum and angular momentum. These properties may all be imparted to matter with which it interacts (through work). EMR is produced from other types of energy when created, and it is converted to other types of energy when it is destroyed. The photon is the quantum of the electromagnetic interaction, and is the basic “unit” or constituent of all forms of EMR. The quantum nature of light becomes more apparent at high frequencies (or high photon energy). Such photons behave more like particles than lower-frequency photons do.

Electromagnetic Wave : Electromagnetic waves can be imagined as a self-propagating transverse oscillating wave of electric and magnetic fields. This 3D diagram shows a plane linearly polarized wave propagating from left to right.

In general, there is a relation of waves which states that the velocity (\(\mathrm{v}\)) of a wave is proportional to the frequency (\(\mathrm{f}\)) times the wavelength (\(\mathrm{λ}\)):

We also know that classical momentum pp is given by p=mvp=mv which relates to force via Newton’s second law: \(\mathrm{F=\dfrac{dp}{dt}}\)

EM waves with higher frequencies carry more energy. This is a direct result of the equations above. Since \(\mathrm{v∝f}\) we find that higher frequencies imply greater velocity. If velocity is increased then we have greater momentum which implies a greater force (it gets a little bit tricky when we talk about particles moving close to the speed of light, but this observation holds in the classical sense). Since energy is the ability of an object to do work, we find that for \(\mathrm{W=Fd}\) a greater force correlates to more energy transfer. Again, this is an easy phenomenon to experience empirically; just stand in front of a faster wave and feel the difference!

• A wave can be thought of as a disturbance or oscillation that travels through space-time, accompanied by a transfer of energy.
• The direction a wave propagates is perpendicular to the direction it oscillates for transverse waves.
• A wave does not move mass in the direction of propagation; it transfers energy.
• Transverse waves oscillate in the z-y plane but travel along the x axis.
• A transverse wave has a speed of propagation given by the equation \(\mathrm{v = fλ}\).
• The direction of energy transfer is perpendicular to the motion of the wave.
• While longitudinal waves oscillate in the direction of propagation, they do not displace mass since the oscillations are small and involve an equilibrium position.
• The longitudinal ‘waves’ can be conceptualized as pulses that transfer energy along the axis of propagation.
• Longitudinal waves can be conceptualized as pressure waves characterized by compression and rarefaction.
• The particles which make up a water wave move in circular paths.
• If the waves move slower than the wind above them, energy is transfered from the wind to the waves.
• The oscillations are greatest on the surface of the wave and become weaker deeper in the fluid.
• The wavelength is the spatial period of the wave.
• The frequency of a wave refers to the number of cycles per unit time and is not to be confused with angular frequency.
• The phase velocity can be expressed as the product of wavelength and frequency.
• Waves which are more massive transfer more energy.
• Waves with greater velocities transfer more energy.
• Energy of a wave is transported in the direction of the waves transportation.
• medium : The material or empty space through which signals, waves or forces pass.
• direction of propagation : The axis along which the wave travels.
• wave : A moving disturbance in the energy level of a field.
• wavelength : The length of a single cycle of a wave, as measured by the distance between one peak or trough of a wave and the next; it is often designated in physics as λ, and corresponds to the velocity of the wave divided by its frequency.
• trough : A long, narrow depression between waves or ridges.
• speed of propagation : The speed at which a wave moves through a medium.
• crest : The ridge or top of a wave.
• transverse wave : Any wave in which the direction of disturbance is perpendicular to the direction of travel.
• rarefaction : a reduction in the density of a material, especially that of a fluid
• Longitudinal : Running in the direction of the long axis of a body.
• compression : to increase in density; the act of compressing, or the state of being compressed; compaction
• phase velocity : The velocity of propagation of a pure sine wave of infinite extent and infinitesimal amplitude.
• group velocity : The propagation velocity of the envelope of a modulated travelling wave, which is considered as the propagation velocity of information or energy contained in it.
• plane wave : A constant-frequency wave whose wavefronts (surfaces of constant phase) are infinite parallel planes of constant peak-to-peak amplitude normal to the phase velocity vector.
• wave speed : The absolute value of the velocity at which the phase of any one frequency component of the wave travels.
• frequency : The quotient of the number of times n a periodic phenomenon occurs over the time t in which it occurs: \(\mathrm{f = \frac{n}{t}}\).
• energy : A quantity that denotes the ability to do work and is measured in a unit dimensioned in mass × distance²/time² (ML²/T²) or the equivalent.
• power : A measure of the rate of doing work or transferring energy.
• work : A measure of energy expended in moving an object; most commonly, force times displacement. No work is done if the object does not move.

LICENSES AND ATTRIBUTIONS

CC LICENSED CONTENT, SHARED PREVIOUSLY

• Curation and Revision. Provided by : Boundless.com. License : CC BY-SA: Attribution-ShareAlike

CC LICENSED CONTENT, SPECIFIC ATTRIBUTION

• Waves. Provided by : Wikipedia. Located at : en.Wikipedia.org/wiki/Waves . License : CC BY-SA: Attribution-ShareAlike
• Wave. Provided by : Wikipedia. Located at : en.Wikipedia.org/wiki/Wave . License : CC BY-SA: Attribution-ShareAlike
• direction of propagation. Provided by : Wikipedia. Located at : en.Wikipedia.org/wiki/direction%20of%20propagation . License : CC BY-SA: Attribution-ShareAlike
• wave. Provided by : Wiktionary. Located at : en.wiktionary.org/wiki/wave . License : CC BY-SA: Attribution-ShareAlike
• medium. Provided by : Wiktionary. Located at : en.wiktionary.org/wiki/medium . License : CC BY-SA: Attribution-ShareAlike
• Simple harmonic motion animation. Provided by : Wikipedia. Located at : en.Wikipedia.org/wiki/File:Simple_harmonic_motion_animation.gif . License : Public Domain: No Known Copyright
• The Wave Equation. Located at : http://www.youtube.com/watch?v=jEEPp0mBCdg . License : Public Domain: No Known Copyright . License Terms : Standard YouTube license
• crest. Provided by : Wiktionary. Located at : en.wiktionary.org/wiki/crest . License : CC BY-SA: Attribution-ShareAlike
• Transverse wave. Provided by : Wikipedia. Located at : en.Wikipedia.org/wiki/Transverse_wave . License : CC BY-SA: Attribution-ShareAlike
• Boundless. Provided by : Boundless Learning. Located at : www.boundless.com//physics/definition/speed-of-propagation . License : CC BY-SA: Attribution-ShareAlike
• wavelength. Provided by : Wiktionary. Located at : en.wiktionary.org/wiki/wavelength . License : CC BY-SA: Attribution-ShareAlike
• trough. Provided by : Wiktionary. Located at : en.wiktionary.org/wiki/trough . License : CC BY-SA: Attribution-ShareAlike
• transverse wave. Provided by : Wiktionary. Located at : en.wiktionary.org/wiki/transverse_wave . License : CC BY-SA: Attribution-ShareAlike
• Wave. Provided by : Wikipedia. Located at : simple.Wikipedia.org/wiki/File:Wave.png . License : Public Domain: No Known Copyright
• Two Types of Waves: Longitudinal vs. Transverse. Located at : http://www.youtube.com/watch?v=PxB8-BVO82g . License : Public Domain: No Known Copyright . License Terms : Standard YouTube license
• ComplexSinInATimeAxe. Provided by : Wikipedia. Located at : en.Wikipedia.org/wiki/File:ComplexSinInATimeAxe.gif . License : Public Domain: No Known Copyright
• Longitudinal wave. Provided by : Wikipedia. Located at : en.Wikipedia.org/wiki/Longitudinal_wave . License : CC BY-SA: Attribution-ShareAlike
• Sound waves. Provided by : Wikipedia. Located at : en.Wikipedia.org/wiki/Sound_waves%23Longitudinal_and_transverse_waves . License : CC BY-SA: Attribution-ShareAlike
• Longitudinal. Provided by : Wiktionary. Located at : en.wiktionary.org/wiki/Longitudinal . License : CC BY-SA: Attribution-ShareAlike
• compression. Provided by : Wiktionary. Located at : en.wiktionary.org/wiki/compression . License : CC BY-SA: Attribution-ShareAlike
• rarefaction. Provided by : Wiktionary. Located at : en.wiktionary.org/wiki/rarefaction . License : CC BY-SA: Attribution-ShareAlike
• funwaves - 5.nLongitudinal wave. Provided by : Wikispaces. Located at : http://funwaves.wikispaces.com/5.+Longitudinal+wave . License : CC BY-SA: Attribution-ShareAlike
• Wave power. Provided by : Wikipedia. Located at : en.Wikipedia.org/wiki/Wave_power . License : CC BY-SA: Attribution-ShareAlike
• Wind wave. Provided by : Wikipedia. Located at : en.Wikipedia.org/wiki/Wind_wave . License : CC BY-SA: Attribution-ShareAlike
• Wave power. Provided by : Wikipedia. Located at : http://en.Wikipedia.org/wiki/Wave_power . License : CC BY-SA: Attribution-ShareAlike
• plane wave. Provided by : Wikipedia. Located at : en.Wikipedia.org/wiki/plane%20wave . License : CC BY-SA: Attribution-ShareAlike
• phase velocity. Provided by : Wiktionary. Located at : en.wiktionary.org/wiki/phase_velocity . License : CC BY-SA: Attribution-ShareAlike
• group velocity. Provided by : Wiktionary. Located at : en.wiktionary.org/wiki/group_velocity . License : CC BY-SA: Attribution-ShareAlike
• Wave. Provided by : Wikipedia. Located at : en.Wikipedia.org/wiki/Wave . License : CC BY: Attribution
• Plane Wave Oblique View. Provided by : Wikimedia. Located at : commons.wikimedia.org/wiki/File:Plane_Wave_Oblique_View.jpg . License : Public Domain: No Known Copyright
• Elliptical trajectory on ripples. Provided by : Wikipedia. Located at : en.Wikipedia.org/wiki/File:Elliptical_trajectory_on_ripples.svg . License : Public Domain: No Known Copyright
• Frequency. Provided by : Wikipedia. Located at : en.Wikipedia.org/wiki/Frequency . License : CC BY-SA: Attribution-ShareAlike
• Phase velocity. Provided by : Wikipedia. Located at : en.Wikipedia.org/wiki/Phase_velocity . License : CC BY-SA: Attribution-ShareAlike
• Group velocity. Provided by : Wikipedia. Located at : en.Wikipedia.org/wiki/Group_velocity . License : CC BY-SA: Attribution-ShareAlike
• wave speed. Provided by : Wikipedia. Located at : en.Wikipedia.org/wiki/wave%20speed . License : CC BY-SA: Attribution-ShareAlike
• frequency. Provided by : Wiktionary. Located at : en.wiktionary.org/wiki/frequency . License : CC BY-SA: Attribution-ShareAlike
• Group velocity. Provided by : Wikipedia. Located at : en.Wikipedia.org/wiki/Group_velocity . License : CC BY: Attribution
• Sine waves different frequencies. Provided by : Wikipedia. Located at : en.Wikipedia.org/wiki/File:Sine_waves_different_frequencies.svg . License : Public Domain: No Known Copyright
• Electromagnetic radiation. Provided by : Wikipedia. Located at : en.Wikipedia.org/wiki/Electromagnetic_radiation . License : CC BY-SA: Attribution-ShareAlike
• Electromagnetic radiation. Provided by : Wikipedia. Located at : http://en.Wikipedia.org/wiki/Electromagnetic_radiation . License : CC BY-SA: Attribution-ShareAlike
• energy. Provided by : Wiktionary. Located at : en.wiktionary.org/wiki/energy . License : CC BY-SA: Attribution-ShareAlike
• work. Provided by : Wiktionary. Located at : en.wiktionary.org/wiki/work . License : CC BY-SA: Attribution-ShareAlike
• Boundless. Provided by : Boundless Learning. Located at : www.boundless.com//sociology/definition/power . License : CC BY-SA: Attribution-ShareAlike
• Wave. Provided by : Wikipedia. Located at : http://simple.Wikipedia.org/wiki/File:Wave.png . License : Public Domain: No Known Copyright
• ComplexSinInATimeAxe. Provided by : Wikipedia. Located at : http://en.Wikipedia.org/wiki/File:ComplexSinInATimeAxe.gif . License : Public Domain: No Known Copyright
• Elliptical trajectory on ripples. Provided by : Wikipedia. Located at : http://en.Wikipedia.org/wiki/File:Elliptical_trajectory_on_ripples.svg . License : Public Domain: No Known Copyright
• Waves in pacifica 1. Provided by : Wikipedia. Located at : en.Wikipedia.org/wiki/File:Waves_in_pacifica_1.jpg . License : Public Domain: No Known Copyright
• Electromagneticwave3Dfromside. Provided by : Wikipedia. Located at : en.Wikipedia.org/wiki/File:Electromagneticwave3Dfromside.gif . License : CC BY: Attribution

Help | Advanced Search

Physics > Optics

Title: an ultra-broadband photonic-chip-based traveling-wave parametric amplifier.

Abstract: Optical amplification, crucial for modern communication, primarily relies on erbium-doped fiber amplifiers (EDFAs) to enhance signals without distortion. However, EDFAs only cover a portion of the low-loss spectrum of optical fibers. Optical parametric amplification, utilizing material nonlinearities, offers expanded capacity, but has faced limitations in gain and bandwidth. Addressing this, we present a high-gain continuous-traveling-wave parametric amplifier, surpassing the erbium gain window. Leveraging low-loss gallium phosphide-on-insulator photonic integrated waveguides, we achieve up to 35 dB of parametric gain, with a fiber-to-fiber net gain exceeding 10 dB across a wide wavelength range of approximately 140 nm centered at 1550 nm. We demonstrate the capability to amplify ultra-weak signals, extending over 6 orders of magnitude of input powers, optical frequency combs, and communication signals, highlighting the practical potential of our photonic-chip-based amplifier.

Submission history

Access paper:.

• HTML (experimental)
• Other Formats

References & Citations

• Google Scholar
• Semantic Scholar

BibTeX formatted citation

Bibliographic and Citation Tools

Code, data and media associated with this article, recommenders and search tools.

• Institution

arXivLabs: experimental projects with community collaborators

arXivLabs is a framework that allows collaborators to develop and share new arXiv features directly on our website.

Both individuals and organizations that work with arXivLabs have embraced and accepted our values of openness, community, excellence, and user data privacy. arXiv is committed to these values and only works with partners that adhere to them.

Have an idea for a project that will add value for arXiv's community? Learn more about arXivLabs .