travelling salesman problem tutorialspoint

• Data Structures & Algorithms
• DSA - Overview
• DSA - Environment Setup
• DSA - Algorithms Basics
• DSA - Asymptotic Analysis
• Data Structures
• DSA - Data Structure Basics
• DSA - Data Structures and Types
• DSA - Array Data Structure
• Linked Lists
• DSA - Linked List Data Structure
• DSA - Doubly Linked List Data Structure
• DSA - Circular Linked List Data Structure
• Stack & Queue
• DSA - Stack Data Structure
• DSA - Expression Parsing
• DSA - Queue Data Structure
• Searching Algorithms
• DSA - Searching Algorithms
• DSA - Linear Search Algorithm
• DSA - Binary Search Algorithm
• DSA - Interpolation Search
• DSA - Jump Search Algorithm
• DSA - Exponential Search
• DSA - Fibonacci Search
• DSA - Sublist Search
• DSA - Hash Table
• Sorting Algorithms
• DSA - Sorting Algorithms
• DSA - Bubble Sort Algorithm
• DSA - Insertion Sort Algorithm
• DSA - Selection Sort Algorithm
• DSA - Merge Sort Algorithm
• DSA - Shell Sort Algorithm
• DSA - Heap Sort
• DSA - Bucket Sort Algorithm
• DSA - Counting Sort Algorithm
• DSA - Radix Sort Algorithm
• DSA - Quick Sort Algorithm
• Graph Data Structure
• DSA - Graph Data Structure
• DSA - Depth First Traversal
• DSA - Breadth First Traversal
• DSA - Spanning Tree
• Tree Data Structure
• DSA - Tree Data Structure
• DSA - Tree Traversal
• DSA - Binary Search Tree
• DSA - AVL Tree
• DSA - Red Black Trees
• DSA - B Trees
• DSA - B+ Trees
• DSA - Splay Trees
• DSA - Tries
• DSA - Heap Data Structure
• DSA - Recursion Algorithms
• DSA - Tower of Hanoi Using Recursion
• DSA - Fibonacci Series Using Recursion
• Divide and Conquer
• DSA - Divide and Conquer
• DSA - Max-Min Problem
• DSA - Strassen's Matrix Multiplication
• DSA - Karatsuba Algorithm
• Greedy Algorithms
• DSA - Greedy Algorithms
• DSA - Travelling Salesman Problem (Greedy Approach)
• DSA - Prim's Minimal Spanning Tree
• DSA - Kruskal's Minimal Spanning Tree
• DSA - Dijkstra's Shortest Path Algorithm
• DSA - Map Colouring Algorithm
• DSA - Fractional Knapsack Problem
• DSA - Job Sequencing with Deadline
• DSA - Optimal Merge Pattern Algorithm
• Dynamic Programming
• DSA - Dynamic Programming
• DSA - Matrix Chain Multiplication
• DSA - Floyd Warshall Algorithm
• DSA - 0-1 Knapsack Problem
• DSA - Longest Common Subsequence Algorithm
• DSA - Travelling Salesman Problem (Dynamic Approach)
• Approximation Algorithms
• DSA - Approximation Algorithms
• DSA - Vertex Cover Algorithm
• DSA - Set Cover Problem
• DSA - Travelling Salesman Problem (Approximation Approach)
• Randomized Algorithms
• DSA - Randomized Algorithms
• DSA - Randomized Quick Sort Algorithm
• DSA - Karger’s Minimum Cut Algorithm
• DSA - Fisher-Yates Shuffle Algorithm
• DSA Useful Resources
• DSA - Questions and Answers
• DSA - Quick Guide
• DSA - Useful Resources
• DSA - Discussion
• Selected Reading
• UPSC IAS Exams Notes
• Developer's Best Practices
• Questions and Answers
• Effective Resume Writing
• HR Interview Questions
• Computer Glossary

Travelling Salesman Problem (Greedy Approach)

Travelling salesperson algorithm.

The travelling salesman problem is a graph computational problem where the salesman needs to visit all cities (represented using nodes in a graph) in a list just once and the distances (represented using edges in the graph) between all these cities are known. The solution that is needed to be found for this problem is the shortest possible route in which the salesman visits all the cities and returns to the origin city.

If you look at the graph below, considering that the salesman starts from the vertex ‘a’, they need to travel through all the remaining vertices b, c, d, e, f and get back to ‘a’ while making sure that the cost taken is minimum.

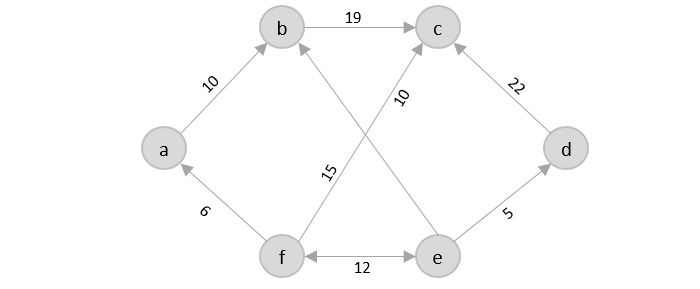
There are various approaches to find the solution to the travelling salesman problem: naive approach, greedy approach, dynamic programming approach, etc. In this tutorial we will be learning about solving travelling salesman problem using greedy approach.

As the definition for greedy approach states, we need to find the best optimal solution locally to figure out the global optimal solution. The inputs taken by the algorithm are the graph G {V, E}, where V is the set of vertices and E is the set of edges. The shortest path of graph G starting from one vertex returning to the same vertex is obtained as the output.

Travelling salesman problem takes a graph G {V, E} as an input and declare another graph as the output (say G’) which will record the path the salesman is going to take from one node to another.

The algorithm begins by sorting all the edges in the input graph G from the least distance to the largest distance.

The first edge selected is the edge with least distance, and one of the two vertices (say A and B) being the origin node (say A).

Then among the adjacent edges of the node other than the origin node (B), find the least cost edge and add it onto the output graph.

Continue the process with further nodes making sure there are no cycles in the output graph and the path reaches back to the origin node A.

However, if the origin is mentioned in the given problem, then the solution must always start from that node only. Let us look at some example problems to understand this better.

Consider the following graph with six cities and the distances between them −

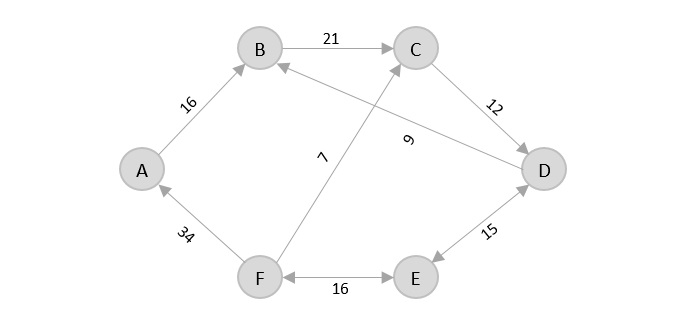
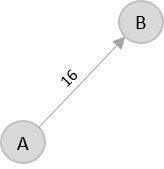
From the given graph, since the origin is already mentioned, the solution must always start from that node. Among the edges leading from A, A → B has the shortest distance.

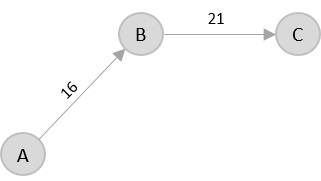
Then, B → C has the shortest and only edge between, therefore it is included in the output graph.

There’s only one edge between C → D, therefore it is added to the output graph.

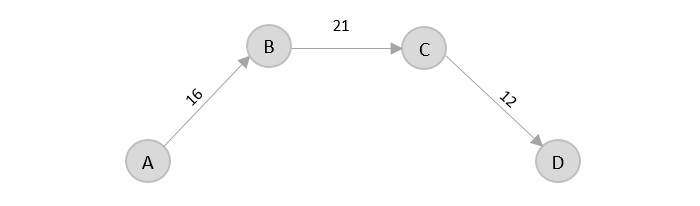
There’s two outward edges from D. Even though, D → B has lower distance than D → E, B is already visited once and it would form a cycle if added to the output graph. Therefore, D → E is added into the output graph.

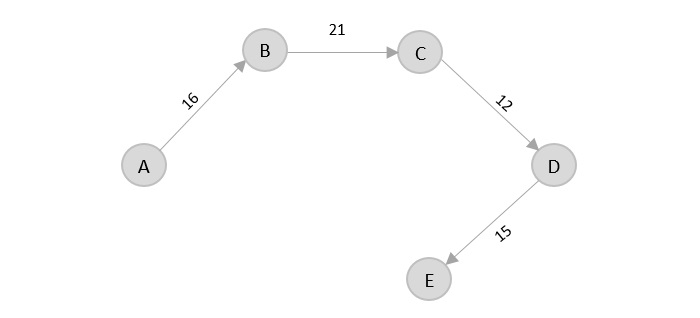
There’s only one edge from e, that is E → F. Therefore, it is added into the output graph.

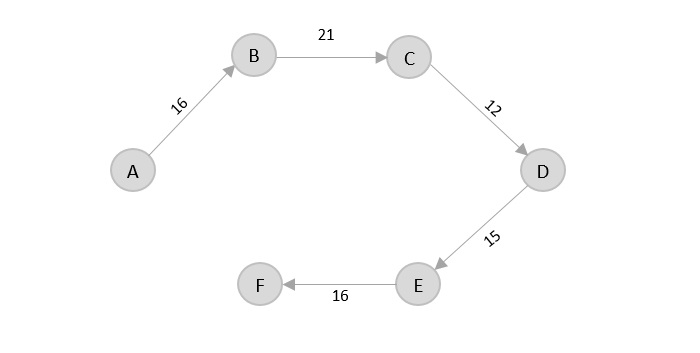
Again, even though F → C has lower distance than F → A, F → A is added into the output graph in order to avoid the cycle that would form and C is already visited once.

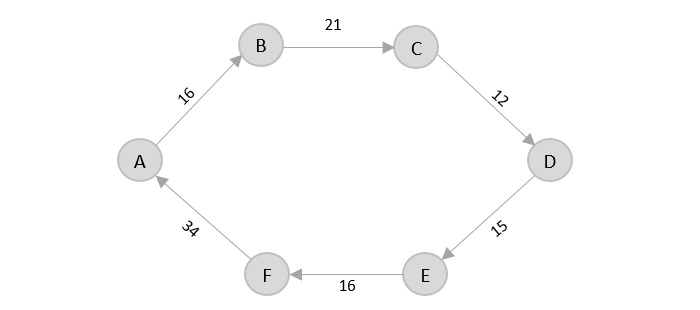
The shortest path that originates and ends at A is A → B → C → D → E → F → A

The cost of the path is: 16 + 21 + 12 + 15 + 16 + 34 = 114.

Even though, the cost of path could be decreased if it originates from other nodes but the question is not raised with respect to that.

The complete implementation of Travelling Salesman Problem using Greedy Approach is given below −

Reset password New user? Sign up

Existing user? Log in

Traveling Salesperson Problem

Already have an account? Log in here.

A salesperson needs to visit a set of cities to sell their goods. They know how many cities they need to go to and the distances between each city. In what order should the salesperson visit each city exactly once so that they minimize their travel time and so that they end their journey in their city of origin?

The traveling salesperson problem is an extremely old problem in computer science that is an extension of the Hamiltonian Circuit Problem . It has important implications in complexity theory and the P versus NP problem because it is an NP-Complete problem . This means that a solution to this problem cannot be found in polynomial time (it takes superpolynomial time to compute an answer). In other words, as the number of vertices increases linearly, the computation time to solve the problem increases exponentially.

The following image is a simple example of a network of cities connected by edges of a specific distance. The origin city is also marked.

Network of cities

Here is the solution for that network, it has a distance traveled of only 14. Any other path that the salesman can takes will result in a path length that is more than 14.

Relationship to Graphs

Special kinds of tsp, importance for p vs np, applications.

The traveling salesperson problem can be modeled as a graph . Specifically, it is typical a directed, weighted graph. Each city acts as a vertex and each path between cities is an edge. Instead of distances, each edge has a weight associated with it. In this model, the goal of the traveling salesperson problem can be defined as finding a path that visits every vertex, returns to the original vertex, and minimizes total weight.

To that end, many graph algorithms can be used on this model. Search algorithms like breadth-first search (BFS) , depth-first search (DFS) , and Dijkstra's shortest path algorithm can certainly be used, however, they do not take into consideration that fact that every vertex must be visited.

The Traveling Salesperson Problem (TSP), an NP-Complete problem, is notoriously complicated to solve. That is because the greedy approach is so computational intensive. The greedy approach to solving this problem would be to try every single possible path and see which one is the fastest. Try this conceptual question to see if you have a grasp for how hard it is to solve.

For a fully connected map with \(n\) cities, how many total paths are possible for the traveling salesperson? Show Answer There are (n-1)! total paths the salesperson can take. The computation needed to solve this problem in this way grows far too quickly to be a reasonable solution. If this map has only 5 cities, there are \(4!\), or 24, paths. However, if the size of this map is increased to 20 cities, there will be \(1.22 \cdot 10^{17}\) paths!

The greedy approach to TSP would go like this:

• Find all possible paths.
• Find the cost of every paths.
• Choose the path with the lowest cost.

Another version of a greedy approach might be: At every step in the algorithm, choose the best possible path. This version might go a little quicker, but it's not guaranteed to find the best answer, or an answer at all since it might hit a dead end.

For NP-Hard problems (a subset of NP-Complete problems) like TSP, exact solutions can only be implemented in a reasonable amount of time for small input sizes (maps with few cities). Otherwise, the best approach we can do is provide a heuristic to help the problem move forward in an optimal way. However, these approaches cannot be proven to be optimal because they always have some sort of downside.

Small input sizes

As described, in a previous section , the greedy approach to this problem has a complexity of \(O(n!)\). However, there are some approaches that decrease this computation time.

The Held-Karp Algorithm is one of the earliest applications of dynamic programming . Its complexity is much lower than the greedy approach at \(O(n^2 2^n)\). Basically what this algorithm says is that every sub path along an optimal path is itself an optimal path. So, computing an optimal path is the same as computing many smaller subpaths and adding them together.

Heuristics are a way of ranking possible next steps in an algorithm in the hopes of cutting down computation time for the entire algorithm. They are often a tradeoff of some attribute - such as completeness, accuracy, or precision - in favor of speed. Heuristics exist for the traveling salesperson problem as well.

The most simple heuristic for this problem is the greedy heuristic. This heuristic simply says, at each step of the network traversal, choose the best next step. In other words, always choose the closest city that you have not yet visited. This heuristic seems like a good one because it is simple and intuitive, and it is even used in practice sometimes, however there are heuristics that are proven to be more effective.

Christofides algorithm is another heuristic. It produces at most 1.5 times the optimal weight for TSP. This algorithm involves finding a minimum spanning tree for the network. Next, it creates matchings for the cities of an odd degree (meaning they have an odd number of edges coming out of them), calculates an eulerian path , and converts back to a TSP path.

Even though it is typically impossible to optimally solve TSP problems, there are cases of TSP problems that can be solved if certain conditions hold.

The metric-TSP is an instance of TSP that satisfies this condition: The distance from city A to city B is less than or equal to the distance from city A to city C plus the distance from city C to city B. Or,

\[distance_{AB} \leq distance_{AC} + distance_{CB}\]

This is a condition that holds in the real world, but it can't always be expected to hold for every TSP problem. But, with this inequality in place, the approximated path will be no more than twice the optimal path. Even better, we can bound the solution to a \(3/2\) approximation by using Christofide's Algorithm .

The euclidean-TSP has an even stricter constraint on the TSP input. It states that all cities' edges in the network must obey euclidean distances . Recent advances have shown that approximation algorithms using euclidean minimum spanning trees have reduced the runtime of euclidean-TSP, even though they are also NP-hard. In practice, though, simpler heuristics are still used.

The P versus NP problem is one of the leading questions in modern computer science. It asks whether or not every problem whose solution can be verified in polynomial time by a computer can also be solved in polynomial time by a computer. TSP, for example, cannot be solved in polynomial time (at least that's what is currently theorized). However, TSP can be solved in polynomial time when it is phrased like this: Given a graph and an integer, x, decide if there is a path of length x or less than x . It's easy to see that given a proposed answer to this question, it is simple to check if it is less than or equal to x.

The traveling salesperson problem, like other problems that are NP-Complete, are very important to this debate. That is because if a polynomial time solution can be found to this problems, then \(P = NP\). As it stands, most scientists believe that \(P \ne NP\).

The traveling salesperson problem has many applications. The obvious ones are in the transportation space. Planning delivery routes or flight patterns, for example, would benefit immensly from breakthroughs is this problem or in the P versus NP problem .

However, this same logic can be applied to many facets of planning as well. In robotics, for instance, planning the order in which to drill holes in a circuit board is a complex task due to the sheer number of holes that must be drawn.

The best and most important application of TSP, however, comes from the fact that it is an NP-Complete problem. That means that its practical applications amount to the applications of any problem that is NP-Complete. So, if there are significant breakthroughs for TSP, that means that those exact same breakthrough can be applied to any problem in the NP-Complete class.

Problem Loading...

Note Loading...

Set Loading...

DSA Tutorial

Linked lists, stacks & queues, hash tables, shortest path, minimum spanning tree, maximum flow, time complexity, dsa reference, dsa examples, dsa the traveling salesman problem.

The Traveling Salesman Problem

The Traveling Salesman Problem states that you are a salesperson and you must visit a number of cities or towns.

Rules : Visit every city only once, then return back to the city you started in.

Goal : Find the shortest possible route.

Except for the Held-Karp algorithm (which is quite advanced and time consuming, (\(O(2^n n^2)\)), and will not be described here), there is no other way to find the shortest route than to check all possible routes.

This means that the time complexity for solving this problem is \(O(n!)\), which means 720 routes needs to be checked for 6 cities, 40,320 routes must be checked for 8 cities, and if you have 10 cities to visit, more than 3.6 million routes must be checked!

Note: "!", or "factorial", is a mathematical operation used in combinatorics to find out how many possible ways something can be done. If there are 4 cities, each city is connected to every other city, and we must visit every city exactly once, there are \(4!= 4 \cdot 3 \cdot 2 \cdot 1 = 24\) different routes we can take to visit those cities.

The Traveling Salesman Problem (TSP) is a problem that is interesting to study because it is very practical, but so time consuming to solve, that it becomes nearly impossible to find the shortest route, even in a graph with just 20-30 vertices.

If we had an effective algorithm for solving The Traveling Salesman Problem, the consequences would be very big in many sectors, like for example chip design, vehicle routing, telecommunications, and urban planning.

Checking All Routes to Solve The Traveling Salesman Problem

To find the optimal solution to The Traveling Salesman Problem, we will check all possible routes, and every time we find a shorter route, we will store it, so that in the end we will have the shortest route.

Good: Finds the overall shortest route.

Bad: Requires an awful lot of calculation, especially for a large amount of cities, which means it is very time consuming.

How it works:

• Check the length of every possible route, one route at a time.
• Is the current route shorter than the shortest route found so far? If so, store the new shortest route.
• After checking all routes, the stored route is the shortest one.

Such a way of finding the solution to a problem is called brute force .

Brute force is not really an algorithm, it just means finding the solution by checking all possibilities, usually because of a lack of a better way to do it.

Speed: {{ inpVal }}

Finding the shortest route in The Traveling Salesman Problem by checking all routes (brute force).

Progress: {{progress}}%

n = {{vertices}} cities

{{vertices}}!={{posRoutes}} possible routes

Show every route: {{showCompares}}

The reason why the brute force approach of finding the shortest route (as shown above) is so time consuming is that we are checking all routes, and the number of possible routes increases really fast when the number of cities increases.

Finding the optimal solution to the Traveling Salesman Problem by checking all possible routes (brute force):

Using A Greedy Algorithm to Solve The Traveling Salesman Problem

Since checking every possible route to solve the Traveling Salesman Problem (like we did above) is so incredibly time consuming, we can instead find a short route by just going to the nearest unvisited city in each step, which is much faster.

Good: Finds a solution to the Traveling Salesman Problem much faster than by checking all routes.

Bad: Does not find the overall shortest route, it just finds a route that is much shorter than an average random route.

• Visit every city.
• The next city to visit is always the nearest of the unvisited cities from the city you are currently in.
• After visiting all cities, go back to the city you started in.

This way of finding an approximation to the shortest route in the Traveling Salesman Problem, by just going to the nearest unvisited city in each step, is called a greedy algorithm .

Finding an approximation to the shortest route in The Traveling Salesman Problem by always going to the nearest unvisited neighbor (greedy algorithm).

As you can see by running this simulation a few times, the routes that are found are not completely unreasonable. Except for a few times when the lines cross perhaps, especially towards the end of the algorithm, the resulting route is a lot shorter than we would get by choosing the next city at random.

Finding a near-optimal solution to the Traveling Salesman Problem using the nearest-neighbor algorithm (greedy):

Other Algorithms That Find Near-Optimal Solutions to The Traveling Salesman Problem

In addition to using a greedy algorithm to solve the Traveling Salesman Problem, there are also other algorithms that can find approximations to the shortest route.

These algorithms are popular because they are much more effective than to actually check all possible solutions, but as with the greedy algorithm above, they do not find the overall shortest route.

Algorithms used to find a near-optimal solution to the Traveling Salesman Problem include:

• 2-opt Heuristic: An algorithm that improves the solution step-by-step, in each step removing two edges and reconnecting the two paths in a different way to reduce the total path length.
• Genetic Algorithm: This is a type of algorithm inspired by the process of natural selection and use techniques such as selection, mutation, and crossover to evolve solutions to problems, including the TSP.
• Simulated Annealing: This method is inspired by the process of annealing in metallurgy. It involves heating and then slowly cooling a material to decrease defects. In the context of TSP, it's used to find a near-optimal solution by exploring the solution space in a way that allows for occasional moves to worse solutions, which helps to avoid getting stuck in local minima.
• Ant Colony Optimization: This algorithm is inspired by the behavior of ants in finding paths from the colony to food sources. It's a more complex probabilistic technique for solving computational problems which can be mapped to finding good paths through graphs.

Time Complexity for Solving The Traveling Salesman Problem

To get a near-optimal solution fast, we can use a greedy algorithm that just goes to the nearest unvisited city in each step, like in the second simulation on this page.

Solving The Traveling Salesman Problem in a greedy way like that, means that at each step, the distances from the current city to all other unvisited cities are compared, and that gives us a time complexity of \(O(n^2) \).

But finding the shortest route of them all requires a lot more operations, and the time complexity for that is \(O(n!)\), like mentioned earlier, which means that for 4 cities, there are 4! possible routes, which is the same as \(4 \cdot 3 \cdot 2 \cdot 1 = 24\). And for just 12 cities for example, there are \(12! = 12 \cdot 11 \cdot 10 \cdot \; ... \; \cdot 2 \cdot 1 = 479,001,600\) possible routes!

See the time complexity for the greedy algorithm \(O(n^2)\), versus the time complexity for finding the shortest route by comparing all routes \(O(n!)\), in the image below.

But there are two things we can do to reduce the number of routes we need to check.

In the Traveling Salesman Problem, the route starts and ends in the same place, which makes a cycle. This means that the length of the shortest route will be the same no matter which city we start in. That is why we have chosen a fixed city to start in for the simulation above, and that reduces the number of possible routes from \(n!\) to \((n-1)!\).

Also, because these routes go in cycles, a route has the same distance if we go in one direction or the other, so we actually just need to check the distance of half of the routes, because the other half will just be the same routes in the opposite direction, so the number of routes we need to check is actually \( \frac{(n-1)!}{2}\).

But even if we can reduce the number of routes we need to check to \( \frac{(n-1)!}{2}\), the time complexity is still \( O(n!)\), because for very big \(n\), reducing \(n\) by one and dividing by 2 does not make a significant change in how the time complexity grows when \(n\) is increased.

To better understand how time complexity works, go to this page .

Actual Traveling Salesman Problems Are More Complex

The edge weight in a graph in this context of The Traveling Salesman Problem tells us how hard it is to go from one point to another, and it is the total edge weight of a route we want to minimize.

So far on this page, the edge weight has been the distance in a straight line between two points. And that makes it much easier to explain the Traveling Salesman Problem, and to display it.

But in the real world there are many other things that affects the edge weight:

• Obstacles: When moving from one place to another, we normally try to avoid obstacles like trees, rivers, houses for example. This means it is longer and takes more time to go from A to B, and the edge weight value needs to be increased to factor that in, because it is not a straight line anymore.
• Transportation Networks: We usually follow a road or use public transport systems when traveling, and that also affects how hard it is to go (or send a package) from one place to another.
• Traffic Conditions: Travel congestion also affects the travel time, so that should also be reflected in the edge weight value.
• Legal and Political Boundaries: Crossing border for example, might make one route harder to choose than another, which means the shortest straight line route might be slower, or more costly.
• Economic Factors: Using fuel, using the time of employees, maintaining vehicles, all these things cost money and should also be factored into the edge weights.

As you can see, just using the straight line distances as the edge weights, might be too simple compared to the real problem. And solving the Traveling Salesman Problem for such a simplified problem model would probably give us a solution that is not optimal in a practical sense.

It is not easy to visualize a Traveling Salesman Problem when the edge length is not just the straight line distance between two points anymore, but the computer handles that very well.

COLOR PICKER

Contact Sales

If you want to use W3Schools services as an educational institution, team or enterprise, send us an e-mail: [email protected]

Report Error

If you want to report an error, or if you want to make a suggestion, send us an e-mail: [email protected]

Top Tutorials

Top references, top examples, get certified.

Ace your Coding Interview

• DSA Problems
• Binary Tree
• Binary Search Tree
• Dynamic Programming
• Divide and Conquer
• Linked List
• Backtracking

Travelling Salesman Problem using Branch and Bound

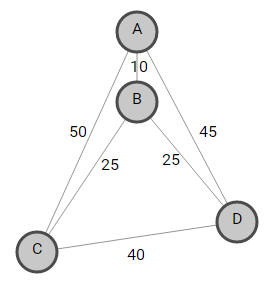
Given a set of cities and the distance between every pair of cities, the problem is to find the shortest possible route that visits every city exactly once and returns to the starting point.

For example, consider the following graph . A TSP tour in the graph is A —> B —> C —> D —> B —> A . The cost of the tour is 10 + 25 + 40 + 25 + 10 = 100 .

This post discusses the Travelling Salesman Problem using Branch and Bound.

  The term Branch and Bound refer to all state-space search methods in which all the children of an E–node are generated before any other live node can become the E–node. E–node is the node, which is being expended. State–space tree can be expended in any method, i.e., BFS or DFS . Both start with the root node and generate other nodes. A node that has been generated and whose children are not yet been expanded is called a live-node. A node is called a dead node, which has been generated, but it cannot be expanded further. In this method, we expand the most promising node, which means the node which promises that expanding or choosing it will give us the optimal solution. So, we prepare the tree starting from the root and then expand it.

We have a cost matrix defined by:

For example, consider the following cost matrix M ,

Following is the state-space tree for the above TSP problem, which shows the optimal solution marked in green:

As we can see from the above diagram, every node has a cost associated with it. When we go from the city i to city j , the cost of a node j will be the sum of the parent node i , the cost of an edge (i, j) , and the lower bound of the path starting at node j .

As the root node is the first node to be expanded, it doesn’t have any parent. So, the cost will be only the lower bound of the path starting at the root.

Now, how do we calculate the lower bound of the path starting at any node?

In general, to get the lower bound of the path starting from the node, we reduce each row and column so that there must be at least one zero in each row and Column. We need to reduce the minimum value from each element in each row and column.

Let’s start from the root node.

We reduce the minimum value in each row from each element in that row. The minimum in each row of cost matrix M is marked by blue [10 2 2 3 4] below.

After reducing the row, we get the below reduced matrix.

We then reduce the minimum value in each column from each element in that column. Minimum in each column is marked by blue [1 0 3 0 0] . After reducing the column, we get below the reduced matrix. This matrix will be further processed by child nodes of the root node to calculate their lower bound.

The total expected cost at the root node is the sum of all reductions.

Since we have discovered the root node C0 , the next node to be expanded can be any node from C1 , C2 , C3 , C4 . Whichever node has a minimum cost will be expanded further. So, we have to find out the expanding cost of each node.

The parent node C0 has below reduced matrix:

Let’s consider an edge from 0 —> 1 .

1. As we add an edge (0, 1) to our search space, set outgoing edges for city 0 to INFINITY and all incoming edges to city 1 to INFINITY . We also set (1, 0) to INFINITY .

So in a reduced matrix of the parent node, change all the elements in row 0 and column 1 and at index (1, 0) to INFINITY (marked in red).

The resulting cost matrix is:

2. We try to calculate the lower bound of the path starting at node 1 using the above resulting cost matrix. The lower bound is 0 as the matrix is already in reduced form, i.e., all rows and all columns have zero value.

Therefore, for node 1, the cost will be:

Let’s consider an edge from 0 —> 2

1. Change all the elements in row 0 and column 2 and at index (2, 0) to INFINITY (marked in red).

2. Now calculate the lower bound of the path starting at node 2 using the approach discussed earlier. The resultant matrix will be:

Therefore, for node 2, the cost will be

Let’s consider an edge from 0 —> 3 .

1. Change all the elements in row 0 and column 3 and at index (3, 0) to INFINITY (marked in red).

2. Now calculate the lower bound of the path starting at node 3 using the approach discussed earlier. The lower bound of the path starting at node 3 is 0 as it is already in reduced form, i.e., all rows and all columns have zero value.

Therefore, for node 3, the cost will be

Similarly, we calculate the cost of 0 —> 4 . Its cost will be 31 .

Now find a live node with the least estimated cost. Live nodes 1 , 2 , 3 , and 4 have costs 35 , 53 , 25 , and 31 , respectively. The minimum among them is node 3 , having cost 25 . So, node 3 will be expanded further, as shown in the state-space tree diagram. After adding its children to the list of live nodes, find a live node with the least cost and expand it. Continue the search till a leaf is encountered in the space search tree. If a leaf is encountered, then the tour is completed, and we will return to the root node.

  Following is the C++ implementation of the above idea:

Download    Run Code

Output: 1 —> 3 3 —> 4 4 —> 2 2 —> 5 5 —> 1   Total cost is 34

  The proposed method, which uses Branch and Bound, is better because it prepares the matrices in different steps. At each step, the cost matrix is calculated. From the initial point, we know that what can be the minimum cost of the tour. The cost of the initial stages is not an exact cost, but it gives some idea because it is the approximated cost. At each step, it gives us a strong reason for which node we should travel the next and which one not. It gives this fact in terms of the cost of expanding a particular node.

  References:

1. https://www.seas.gwu.edu/~bell/csci212/Branch_and_Bound.pdf 2. http://research.ijcaonline.org/volume65/number5/pxc3885866.pdf

Find minimum path sum in a triangle-shaped matrix

Rate this post

Average rating 4.91 /5. Vote count: 104

No votes so far! Be the first to rate this post.

We are sorry that this post was not useful for you!

Tell us how we can improve this post?

Thanks for reading.

To share your code in the comments, please use our online compiler that supports C, C++, Java, Python, JavaScript, C#, PHP, and many more popular programming languages.

Like us? Refer us to your friends and support our growth. Happy coding :)

Or search by topic

Number and algebra

• The Number System and Place Value
• Calculations and Numerical Methods
• Fractions, Decimals, Percentages, Ratio and Proportion
• Properties of Numbers
• Patterns, Sequences and Structure
• Algebraic expressions, equations and formulae
• Coordinates, Functions and Graphs

Geometry and measure

• Angles, Polygons, and Geometrical Proof
• 3D Geometry, Shape and Space
• Measuring and calculating with units
• Transformations and constructions
• Pythagoras and Trigonometry
• Vectors and Matrices

Probability and statistics

• Handling, Processing and Representing Data
• Probability

Working mathematically

• Thinking mathematically
• Mathematical mindsets
• Cross-curricular contexts
• Physical and digital manipulatives

For younger learners

• Early Years Foundation Stage

Advanced mathematics

• Decision Mathematics and Combinatorics
• Advanced Probability and Statistics

Travelling Salesman

• Getting Started
• Student Solutions
• Teachers' Resources

Andrei from Tudor Vianu National College in Bucharest sent in a comprehensive solution:

First I observed that, for Hamiltonian circuits, the starting point does not matter and any point could be considered as the starting point.

For the first circuit, I considered A as the starting point.

I found the following 6 Hamiltonian circuits (3 loops which can be travelled in two directions each):

A - B - D - E - F - C - A A - C - F - E - D - B - A A - C - B - D - E - F - A A - F - E - D - B - C - A

If the starting point and the direction matter, then there are 3 x 2 x 6 = 36 circuits

(x 2 because there are 2 directions on each path, and x 6because there are 6 possible starting points).

For the second circuit, I found the following Hamiltonian circuits starting at A:

(16 distinct loops which can be travelled in two directions each).

If the direction and starting point are considered, then there are 16 x 2 x 8 = 256 Hamiltonian circuits.

Now, for the salesman's problem, he must return home. This is a classical problem, known under the name TSP (Travelling Salesperson Problem).

Because usually there are a lot of cities to be visited, and consequently a lot of routes (if n is the number of cities, than there are (n-1)!/2 routes, as explained at the end of the solution), it is impossible to investigate all closed paths, where the starting and finishing points are the same, to count distances and to choose.

There are some algorithms for this type of problem that can help. I'll apply the Nearest Neighbour Algorithm, and compare the result with the counted distances.

Nearest Neighbour Algorithm

The Nearest Neighbour Algorithm works as follows:

1. Choose any city as a starting point. Call this city 'a'.

2. Visit the nearest city to city 'a', which we shall call city 'b'. City 'b' becomes the 'current city'.

3. Visit the nearest city to city 'b' which has not yet been visited - city 'c'. City 'c' is now the 'current city'.

4. As per point 3, repeatedly visit the nearest unvisited city to the current city until all cities have been visited once.

5. Once all cities have been visited once, return from the last city to have been visited to the starting city - city 'a'.

Starting Point: A

Using the Nearest Neighbour Algorithm I have found a minimum distance of 480 units.

For this problem, there are 3! = 6 possible Hamilton circuits that start at A, and it is not so difficult to count them all:

ABCDA = ADCBA 480

ABDCA = ACDBA 470

ACBDA = ADBCA 490

The shortest trip is ABDCA or ACDBA, i.e. 470 units, an improvement on the result arrived at using the Nearest Neighbour Algorithm.

[The number of distinct routes for n cities is (n-1)!/2. This is so because for the first stage of the journey the salesman has (n-1) possible routes. For the next there are (n-2) and so on. This gives a total of (n-1)!. But, half the routes will be the reverse of the others, so we must divide by 2. For 4 cities this means 3!/2 = 3 paths, as above.]

• Trending Now
• Foundational Courses
• Data Science
• Practice Problem
• Machine Learning
• System Design
• DevOps Tutorial

Travelling Salesman Problem (TSP): Given a set of cities and the distance between every pair of cities, the problem is to find the shortest possible route that visits every city exactly once and returns to the starting point. Note the difference between Hamiltonian Cycle and TSP.

 The Hamiltonian cycle problem is to find if there exists a tour that visits every city exactly once. Here we know that Hamiltonian Tour exists (because the graph is complete) and in fact, many such tours exist, the problem is to find a minimum weight Hamiltonian Cycle.

Travelling Salesman Problem : https://www.geeksforgeeks.org/travelling-salesman-problem-set-1/

• Design Pattern
• Interview Q

C Control Statements

C functions, c dynamic memory, c structure union, c file handling, c preprocessor, c command line, c programming test, c interview.

• Send your Feedback to [email protected]

Help Others, Please Share

Learn Latest Tutorials

Transact-SQL

Reinforcement Learning

R Programming

React Native

Python Design Patterns

Python Pillow

Python Turtle

Preparation

Verbal Ability

Interview Questions

Company Questions

Trending Technologies

Artificial Intelligence

Cloud Computing

Data Science

Machine Learning

B.Tech / MCA

Data Structures

Operating System

Computer Network

Compiler Design

Computer Organization

Discrete Mathematics

Ethical Hacking

Computer Graphics

Software Engineering

Web Technology

Cyber Security

C Programming

Control System

Data Mining

Data Warehouse