chinese postman tour

• Data Structures
• Linked List
• Binary Tree
• Binary Search Tree
• Segment Tree
• Disjoint Set Union
• Fenwick Tree
• Red-Black Tree
• Advanced Data Structures
• Graph Data Structure And Algorithms
• Introduction to Graphs - Data Structure and Algorithm Tutorials
• Graph and its representations
• Types of Graphs with Examples
• Basic Properties of a Graph
• Applications, Advantages and Disadvantages of Graph
• Transpose graph
• Difference Between Graph and Tree

BFS and DFS on Graph

• Breadth First Search or BFS for a Graph
• Depth First Search or DFS for a Graph
• Applications, Advantages and Disadvantages of Depth First Search (DFS)
• Applications, Advantages and Disadvantages of Breadth First Search (BFS)
• Iterative Depth First Traversal of Graph
• BFS for Disconnected Graph
• Transitive Closure of a Graph using DFS
• Difference between BFS and DFS

Cycle in a Graph

• Detect Cycle in a Directed Graph
• Detect cycle in an undirected graph
• Detect Cycle in a directed graph using colors
• Detect a negative cycle in a Graph | (Bellman Ford)
• Cycles of length n in an undirected and connected graph
• Detecting negative cycle using Floyd Warshall
• Clone a Directed Acyclic Graph

Shortest Paths in Graph

• How to find Shortest Paths from Source to all Vertices using Dijkstra's Algorithm
• Bellman–Ford Algorithm
• Floyd Warshall Algorithm
• Johnson's algorithm for All-pairs shortest paths
• Shortest Path in Directed Acyclic Graph
• Multistage Graph (Shortest Path)
• Shortest path in an unweighted graph
• Karp's minimum mean (or average) weight cycle algorithm
• 0-1 BFS (Shortest Path in a Binary Weight Graph)
• Find minimum weight cycle in an undirected graph

Minimum Spanning Tree in Graph

• Kruskal’s Minimum Spanning Tree (MST) Algorithm
• Difference between Prim's and Kruskal's algorithm for MST
• Applications of Minimum Spanning Tree
• Total number of Spanning Trees in a Graph
• Minimum Product Spanning Tree
• Reverse Delete Algorithm for Minimum Spanning Tree

Topological Sorting in Graph

• Topological Sorting
• All Topological Sorts of a Directed Acyclic Graph
• Kahn's algorithm for Topological Sorting
• Maximum edges that can be added to DAG so that it remains DAG
• Longest Path in a Directed Acyclic Graph
• Topological Sort of a graph using departure time of vertex

Connectivity of Graph

• Articulation Points (or Cut Vertices) in a Graph
• Biconnected Components
• Bridges in a graph
• Eulerian path and circuit for undirected graph
• Fleury's Algorithm for printing Eulerian Path or Circuit
• Strongly Connected Components
• Count all possible walks from a source to a destination with exactly k edges
• Euler Circuit in a Directed Graph
• Word Ladder (Length of shortest chain to reach a target word)
• Find if an array of strings can be chained to form a circle | Set 1
• Tarjan's Algorithm to find Strongly Connected Components
• Paths to travel each nodes using each edge (Seven Bridges of Königsberg)
• Dynamic Connectivity | Set 1 (Incremental)

Maximum flow in a Graph

• Max Flow Problem Introduction
• Ford-Fulkerson Algorithm for Maximum Flow Problem
• Find maximum number of edge disjoint paths between two vertices
• Find minimum s-t cut in a flow network
• Maximum Bipartite Matching
• Channel Assignment Problem
• Introduction to Push Relabel Algorithm
• Introduction and implementation of Karger's algorithm for Minimum Cut
• Dinic's algorithm for Maximum Flow

Some must do problems on Graph

• Find size of the largest region in Boolean Matrix
• Count number of trees in a forest
• A Peterson Graph Problem
• Clone an Undirected Graph
• Introduction to Graph Coloring
• Traveling Salesman Problem (TSP) Implementation
• Introduction and Approximate Solution for Vertex Cover Problem
• Erdos Renyl Model (for generating Random Graphs)

Chinese Postman or Route Inspection | Set 1 (introduction)

• Hierholzer's Algorithm for directed graph
• Boggle (Find all possible words in a board of characters) | Set 1
• Hopcroft–Karp Algorithm for Maximum Matching | Set 1 (Introduction)
• Construct a graph from given degrees of all vertices
• Determine whether a universal sink exists in a directed graph
• Number of sink nodes in a graph
• Two Clique Problem (Check if Graph can be divided in two Cliques)

Chinese Postman Problem is a variation of Eulerian circuit problem for undirected graphs. An Euler Circuit is a closed walk that covers every edge once starting and ending position is same. Chinese Postman problem is defined for connected and undirected graph. The problem is to find shortest path or circuity that visits every edge of the graph at least once. 

If input graph contains Euler Circuit, then a solution of the problem is Euler Circuit   An undirected and connected graph has Eulerian cycle if “ all vertices have even degree “.   

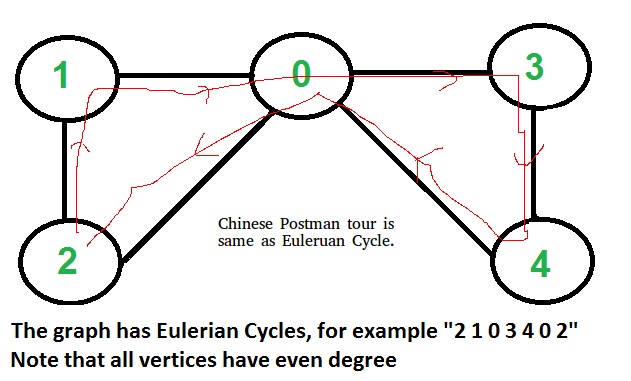
It doesn’t matter whether graph is weighted or unweighted, the Chinese Postman Route is always same as Eulerian Circuit if it exists. In weighted graph the minimum possible weight of Postman tour is sum of all edge weights which we get through Eulerian Circuit. We can’t get a shorter route as we must visit all edges at-least once. 

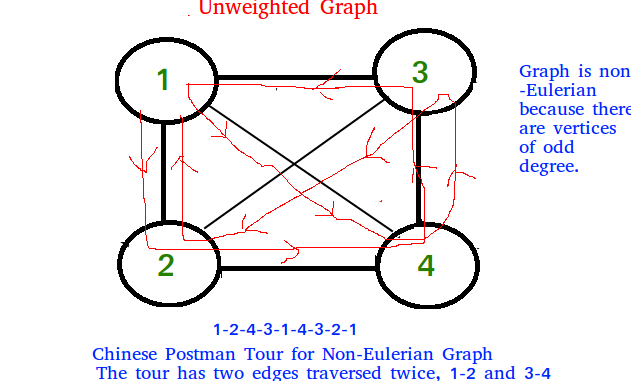
  If input graph does NOT contain Euler Circuit  

In this case, the task reduces to following. 

1) In unweighted graph, minimum number of edges to duplicate so that the given graph converts to a graph with Eulerian Cycle. 

2) In weighted graph, minimum total weight of edges to duplicate so that given graph converts to a graph with Eulerian Cycle.

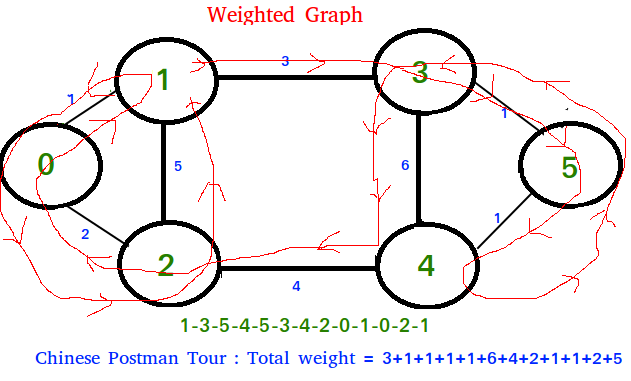
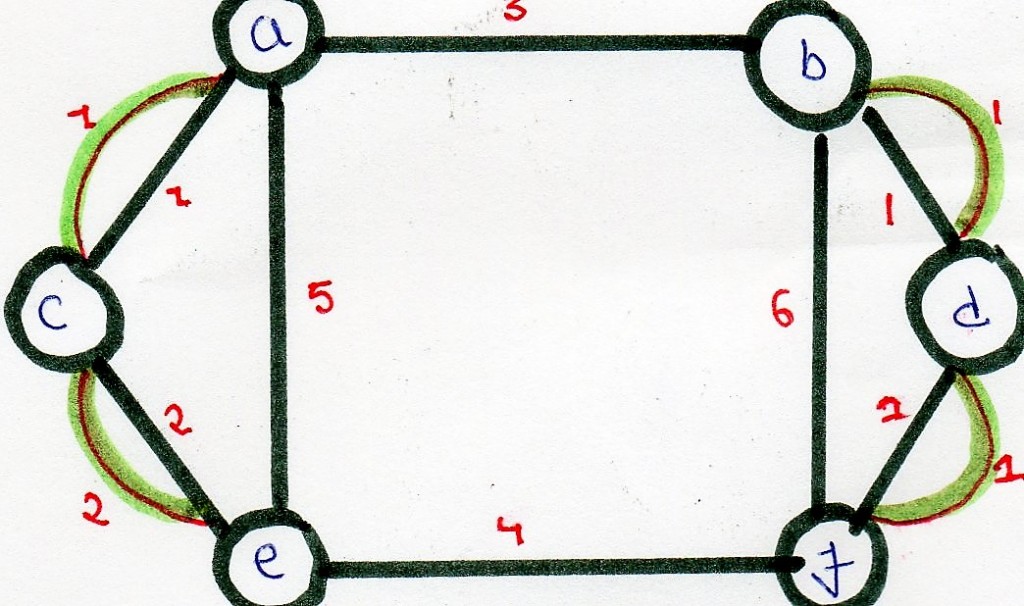
Illustration :  

Please Login to comment...

Similar reads.

• Euler-Circuit

Improve your Coding Skills with Practice

What kind of Experience do you want to share?

Chinese Postman Problem

Introduction

In the 18th century, there is a town called Königsberg, in which there were seven bridges that spanned a forked river that flows past an island. One day a man who wish to walk along each bridge, but that bridge must only traverse exactly once. The man think: "Do there exist such a continuous tour which satifiy the requirement?" This long-standing problem was solved in 1735 in an ingenious way by the Swiss mathematician Leonhard Euler (1707-1782). His solution, and his generalisation of the problem to an arbitrary number of islands and bridges, gave rise to a very important branch of mathematics called Graph Theory [1]

A similar problem is called Chinese Postman Problem (after the Chinese mathematician, Kwan Mei-Ko, who discovered it in early 1960's). The background of Chinese postman problem is interesting. It is the problem that the Chinese Postman faces: he wishes to travel along every road in a city in order to deliver letters, with the least possible distance. The problem is how to find a shortest closed walk of the graph in which each edge is traversed at least once , rather than exactly once. In graph theory, an Euler cycle in a connected, weighted graph is called the Chinese Postman problem.

Graph theory

Graph theory is very useful in solving the Chinese Postman Problem. A graph consists of a non-empty set of points (vertices) and a set of lines (edges) connecting the vertices. The number of edges linked to a vertex is called the degree of that vertex. A walk, which starts at a vertex, traces each edge exactly once and ends at the starting vertex, is called an Euler Trail . If it ends at some other vertex, it is called an open Euler trail . The Königsberg Bridges problem was an attempt to find an open Euler trail.

An open Euler trail is possible if and only if there are exactly two vertices of odd degree. An Euler trail is possible if and only if every vertex is of even degree.

For the practical situation, the problems like delivery of mail or newspaper, trash pick-up, and snow removal can be modeled by Chinese Postman Problem. The problem can be solved in polynomial time if all edges of the graph are undirected.

Solution to Chinese Postman Problem

In case that there are exactly two odd-degree vertices, as shown in figure 1, the problem gets somewhat more difficult. We have to construct a shortest path between the two odd-degree vertices.

Let's consider the graph in figure 1. The problem we shall consider for this graph is how do we start at vertex A, cover every edge in the graph at least once and end at A? An Euler trail does not exist for this graph because there are two odd-degree vertices (i.e. Open Euler trail). Notice that connecting the odd degree vertices B and F by the additional edge is not allowed. Just like we cannot just build the roads or bridges in here and there in real situation. We have to try to minimize cost or distance here, rather than building the new roads. What we can do is retrace steps though; we can go down the same edge more than once.

We cannot add an edge between the two odd-degree vertices, but we can construct a path between them using existing edges in the graph. If we can find the shortest path between these two edges, we will have found the edges that we will want to retrace in our tour, because we want the path that makes us cover edges more than once to be as short as possible.

It is quite easy to find a shortest path from B to F by simple inspection. Let's list all the possible paths below:

E-A-B-D :15

E-C-F-D :10

E-C-B-D :11

It looks like we'll be considering the path given by: E-C-B-D for adding to the graph. It is the shortest path from vertex e to d. We shall call this path m.

In Figure 2 the edges of m in P is doubled. That means that E and F are now both of even degree.

Now it's time to construct an Euler tour from A. The algorithm will consider the double paths between the vertices in path m and produce a tour that can start and end at A. The tour will just cover the edges in m twice instead of once. Let's calculate the total weight of the tour. To begin with, the total weight of all the edges of graph P was 62. The weight of m (the minimal path connecting E and F) is 13. Therefore the shortest postman tour has a weight of 75

Application of Chinese Postman Problem

The practical example is planning of bus routing. In order to save the cost on the fuel, the bus company have modelled the bus stop as the vertix and the road as the edge in the bus route, then using the graph theory to obtain the optimal route that can meet the target of using the minimal fuel but across every road, at least once.

Other application includes trash collection, road sweeping, snow-plows, highway lawnmowers, transmission line inspections, school bus routing, etc.

andrew brooks

Data science side projects, thoughts & experiments, intro to graph optimization: solving the chinese postman problem.

This post was originally published as a tutorial for DataCamp here on September 12 2017 using NetworkX 1.11 . On September 20 2017, NetworkX announced the release of a new version 2.0 , after two years in the making. While 2.0 introduces lots of great features (some have already been used to improve this project in postman_problems ), it also introduced backwards incompatible API changes that broke the original tutorial :(. I’ve commented out lines deprecated by 2.0 and tagged with # deprecated after NX 1.11 , so the changes made here are explicit. Most of the changes are around the passing and setting of attributes and return values deprecating lists for generators.

• This is the NetworkX 2.0 compatible version of the Chinese Postman DataCamp tutorial originally posted here .
• The ideas introduced in this tutorial are packaged into the postman_problems library which is the mature implementation of these concepts.

A note on the making of this post . The original post was created in a Jupyter notebook and converted to HTML with some style tweaks by the DataCamp publishing team. This post was converted from an updated notebook to a Jekyll flavored markdown document for my blog using nb2jekyll with just a few tweaks of my own . This was the first Jupyter notebook I’ve converted to a blog post, but the conversion was smoother than I might have expected. I would recommend nb2jekyll and this post to comrade Jekyll bloggers looking to generate posts directly from Jupyter notebooks.

Intro to Graph Optimization with NetworkX in Python

• Solving the Chinese Postman Problem

With this tutorial, you’ll tackle an established problem in graph theory called the Chinese Postman Problem. There are some components of the algorithm that while conceptually simple, turn out to be computationally rigorous. However, for this tutorial, only some prior knowledge of Python is required: no rigorous math, computer science or graph theory background is needed.

This tutorial will first go over the basic building blocks of graphs (nodes, edges, paths, etc) and solve the problem on a real graph (trail network of a state park) using the NetworkX library in Python. You’ll focus on the core concepts and implementation. For the interested reader, further reading on the guts of the optimization are provided.

The Problem

Personal motivation, networkx: graph manipulation and analysis, installing packages, note on generating the node & edge lists, create graph, summary stats, manipulate colors and layout, overview of cpp algorithm, assumptions and simplifications, cpp step 1: find nodes of odd degree, step 2.1: compute node pairs, step 2.2: compute shortest paths between node pairs, step 2.3: create complete graph, step 2.4: compute minimum weight matching, step 2.5: augment the original graph, naive circuit, correct circuit, create cpp graph, visualization 1: retracing steps, visualization 2: cpp solution sequence, visualization 3: movie, motivating graph optimization.

You’ve probably heard of the Travelling Salesman Problem which amounts to finding the shortest route (say, roads) that connects a set of nodes (say, cities). Although lesser known, the Chinese Postman Problem (CPP), also referred to as the Route Inspection or Arc Routing problem, is quite similar. The objective of the CPP is to find the shortest path that covers all the links (roads) on a graph at least once. If this is possible without doubling back on the same road twice, great; That’s the ideal scenario and the problem is quite simple. However, if some roads must be traversed more than once, you need some math to find the shortest route that hits every road at least once with the lowest total mileage.

(The following is a personal note: cheesy, cheeky and 100% not necessary for learning graph optimization in Python)

I had a real-life application for solving this problem: attaining the rank of Giantmaster Marathoner.

What is a Giantmaster? A Giantmaster is one (canine or human) who has hiked every trail of Sleeping Giant State Park in Hamden CT (neighbor to my hometown of Wallingford)… in their lifetime. A Giantmaster Marathoner is one who has hiked all these trails in a single day.

Thanks to the fastidious record keeping of the Sleeping Giant Park Association, the full roster of Giantmasters and their level of Giantmastering can be found here . I have to admit this motivated me quite a bit to kick-start this side-project and get out there to run the trails. While I myself achieved Giantmaster status in the winter of 2006 when I was a budding young volunteer of the Sleeping Giant Trail Crew (which I was pleased to see recorded in the SG archive ), new challenges have since arisen. While the 12-month and 4-season Giantmaster categories are impressive and enticing, they’d also require more travel from my current home (DC) to my formative home (CT) than I could reasonably manage… and they’re not as interesting for graph optimization, so Giantmaster Marathon it is!

For another reference, the Sleeping Giant trail map is provided below:

Introducing Graphs

The nice thing about graphs is that the concepts and terminology are generally intuitive. Nonetheless, here’s some of the basic lingo:

Graphs are structures that map relations between objects. The objects are referred to as nodes and the connections between them as edges in this tutorial. Note that edges and nodes are commonly referred to by several names that generally mean exactly the same thing:

The starting graph is undirected . That is, your edges have no orientation: they are bi-directional . For example: A<--->B == B<--->A . By contrast, the graph you might create to specify the shortest path to hike every trail could be a directed graph , where the order and direction of edges matters. For example: A--->B != B--->A .

The graph is also an edge-weighted graph where the distance (in miles) between each pair of adjacent nodes represents the weight of an edge. This is handled as an edge attribute named “distance”.

Degree refers to the number of edges incident to (touching) a node. Nodes are referred to as odd-degree nodes when this number is odd and even-degree when even.

The solution to this CPP problem will be a Eulerian tour : a graph where a cycle that passes through every edge exactly once can be made from a starting node back to itself (without backtracking). An Euler Tour is also known by several names:

A matching is a subset of edges in which no node occurs more than once. A minimum weight matching finds the matching with the lowest possible summed edge weight.

NetworkX is the most popular Python package for manipulating and analyzing graphs. Several packages offer the same basic level of graph manipulation, notably igraph which also has bindings for R and C++. However, I found that NetworkX had the strongest graph algorithms that I needed to solve the CPP.

If you’ve done any sort of data analysis in Python or have the Anaconda distribution, my guess is you probably have pandas and matplotlib . However, you might not have networkx . These should be the only dependencies outside the Python Standard Library that you’ll need to run through this tutorial. They are easy to install with pip :

These should be all the packages you’ll need for now. imageio and numpy are imported at the very end to create the GIF animation of the CPP solution. The animation is embedded within this post, so these packages are optional.

The edge list is a simple data structure that you’ll use to create the graph. Each row represents a single edge of the graph with some edge attributes.

• node1 & node2: names of the nodes connected.
• trail: edge attribute indicating the abbreviated name of the trail for each edge. For example: rs = red square
• distance: edge attribute indicating trail length in miles.
• color : trail color used for plotting.
• estimate: edge attribute indicating whether the edge distance is estimated from eyeballing the trailmap ( 1=yes , 0=no ) as some distances are not provided. This is solely for reference; it is not used for analysis.

Node lists are usually optional in networkx and other graph libraries when edge lists are provided because the node names are provided in the edge list’s first two columns. However, in this case, there are some node attributes that we’d like to add: X, Y coordinates of the nodes (trail intersections) so that you can plot your graph with the same layout as the trail map.

I spent an afternoon annotating these manually by tracing over the image with GIMP :

• id: name of the node corresponding to node1 and node2 in the edge list.
• X: horizontal position/coordinate of the node relative to the topleft.
• Y vertical position/coordinate of the node relative to the topleft.

Creating the node names also took some manual effort. Each node represents an intersection of two or more trails. Where possible, the node is named by trail1_trail2 where trail1 precedes trail2 in alphabetical order.

Things got a little more difficult when the same trails intersected each other more than once. For example, the Orange and White trail. In these cases, I appended a _2 or _3 to the node name. For example, you have two distinct node names for the two distinct intersections of Orange and White: o_w and o_w_2 .

This took a lot of trial and error and comparing the plots generated with X,Y coordinates to the real trail map.

Now you use the edge list and the node list to create a graph object in networkx .

Loop through the rows of the edge list and add each edge and its corresponding attributes to graph g .

To illustrate what’s happening here, let’s print the values from the last row in the edge list that got added to graph g :

Similarly, you loop through the rows in the node list and add these node attributes.

Here’s an example from the last row of the node list:

Inspect Graph

Your graph edges are represented by a list of tuples of length 3. The first two elements are the node names linked by the edge. The third is the dictionary of edge attributes.

Similarly, your nodes are represented by a list of tuples of length 2. The first element is the node ID, followed by the dictionary of node attributes.

Print out some summary statistics before visualizing the graph.

Positions: First you need to manipulate the node positions from the graph into a dictionary. This will allow you to recreate the graph using the same layout as the actual trail map. Y is negated to transform the Y-axis origin from the topleft to the bottomleft.

Colors: Now you manipulate the edge colors from the graph into a simple list so that you can visualize the trails by their color.

Now you can make a nice plot that lines up nicely with the Sleeping Giant trail map:

This graph representation obviously doesn’t capture all the trails’ bends and squiggles, however not to worry: these are accurately captured in the edge distance attribute which is used for computation. The visual does capture distance between nodes (trail intersections) as the crow flies, which appears to be a decent approximation.

OK, so now that you’ve defined some terms and created the graph, how do you find the shortest path through it?

Solving the Chinese Postman Problem is quite simple conceptually:

Find all nodes with odd degree (very easy). (Find all trail intersections where the number of trails touching that intersection is an odd number)

Add edges to the graph such that all nodes of odd degree are made even. These added edges must be duplicates from the original graph (we’ll assume no bushwhacking for this problem). The set of edges added should sum to the minimum distance possible (hard…np-hard to be precise). (In simpler terms, minimize the amount of double backing on a route that hits every trail)

Given a starting point, find the Eulerian tour over the augmented dataset (moderately easy). (Once we know which trails we’ll be double backing on, actually calculate the route from beginning to end)

While a shorter and more precise path could be generated by relaxing the assumptions below, this would add complexity beyond the scope of this tutorial which focuses on the CPP.

Assumption 1: Required trails only

As you can see from the trail map above, there are roads along the borders of the park that could be used to connect trails, particularly the red trails. There are also some trails (Horseshoe and unmarked blazes) which are not required per the Giantmaster log , but could be helpful to prevent lengthy double backing. The inclusion of optional trails is actually an established variant of the CPP called the Rural Postman Problem . We ignore optional trails in this tutorial and focus on required trails only.

Assumption 2: Uphill == downhill

The CPP assumes that the cost of walking a trail is equivalent to its distance, regardless of which direction it is walked. However, some of these trails are rather hilly and will require more energy to walk up than down. Some metric that combines both distance and elevation change over a directed graph could be incorporated into an extension of the CPP called the Windy Postman Problem .

Assumption 3: No parallel edges (trails)

While possible, the inclusion of parallel edges (multiple trails connecting the same two nodes) adds complexity to computation. Luckily this only occurs twice here (Blue <=> Red Diamond and Blue <=> Tower Trail). This is addressed by a bit of a hack to the edge list: duplicate nodes are included with a _dupe suffix to capture every trail while maintaining uniqueness in the edges. The CPP implementation in the postman_problems package I wrote robustly handles parallel edges in a more elegant way if you’d like to solve the CPP on your own graph with many parallel edges.

This is a pretty straightforward counting computation. You see that 36 of the 76 nodes have odd degree. These are mostly the dead-end trails (degree 1) and intersections of 3 trails. There are a handful of degree 5 nodes.

CPP Step 2: Find Min Distance Pairs

This is really the meat of the problem. You’ll break it down into 5 parts:

• Compute all possible pairs of odd degree nodes.
• Compute the shortest path between each node pair calculated in 1.
• Create a complete graph connecting every node pair in 1. with shortest path distance attributes calculated in 2.
• Compute a minimum weight matching of the graph calculated in 3. (This boils down to determining how to pair the odd nodes such that the sum of the distance between the pairs is as small as possible).
• Augment the original graph with the shortest paths between the node pairs calculated in 4.

You use the itertools combination function to compute all possible pairs of the odd degree nodes. Your graph is undirected, so we don’t care about order: For example, (a,b) == (b,a) .

Let’s confirm that this number of pairs is correct with a the combinatoric below. Luckily, you only have 630 pairs to worry about. Your computation time to solve this CPP example is trivial (a couple seconds).

However, if you had 3,600 odd node pairs instead, you’d have ~6.5 million pairs to optimize. That’s a ~10,000x increase in output given a 100x increase in input size.

This is the first step that involves some real computation. Luckily networkx has a convenient implementation of Dijkstra’s algorithm to compute the shortest path between two nodes. You apply this function to every pair (all 630) calculated above in odd_node_pairs .

A complete graph is simply a graph where every node is connected to every other node by a unique edge.

Here’s a basic example from Wikipedia of a 7 node complete graph with 21 (7 choose 2) edges:

The graph you create below has 36 nodes and 630 edges with their corresponding edge weight (distance).

create_complete_graph is defined to calculate it. The flip_weights parameter is used to transform the distance to the weight attribute where smaller numbers reflect large distances and high numbers reflect short distances. This sounds a little counter intuitive, but is necessary for Step 2.4 where you calculate the minimum weight matching on the complete graph.

Ideally you’d calculate the minimum weight matching directly, but NetworkX only implements a max_weight_matching function which maximizes, rather than minimizes edge weight. We hack this a bit by negating (multiplying by -1) the distance attribute to get weight . This ensures that order and scale by distance are preserved, but reversed.

For a visual prop, the fully connected graph of odd degree node pairs is plotted below. Note that you preserve the X, Y coordinates of each node, but the edges do not necessarily represent actual trails. For example, two nodes could be connected by a single edge in this graph, but the shortest path between them could be 5 hops through even degree nodes (not shown here).

This is the most complex step in the CPP. You need to find the odd degree node pairs whose combined sum (of distance between them) is as small as possible. So for your problem, this boils down to selecting the optimal 18 edges (36 odd degree nodes / 2) from the hairball of a graph generated in 2.3 .

Both the implementation and intuition of this optimization are beyond the scope of this tutorial… like 800+ lines of code and a body of academic literature beyond this scope.

However, a quick aside for the interested reader:

A huge thanks to Joris van Rantwijk for writing the orginal implementation on his blog way back in 2008. I stumbled into the problem a similar way with the same intention as Joris. From Joris’s 2008 post:

Since I did not find any Perl implementations of maximum weighted matching, I lightly decided to write some code myself. It turned out that I had underestimated the problem, but by the time I realized my mistake, I was so obsessed with the problem that I refused to give up.

However, I did give up. Luckily Joris did not.

This Maximum Weight Matching has since been folded into and maintained within the NetworkX package. Another big thanks to the 10+ contributors on GitHub who have maintained this hefty codebase.

This is a hard and intensive computation. The first breakthrough in 1965 proved that the Maximum Matching problem could be solved in polynomial time. It was published by Jack Edmonds with perhaps one of the most beautiful academic paper titles ever: “Paths, trees, and flowers” [ 1 ]. A body of literature has since built upon this work, improving the optimization procedure. The code implemented in the NetworkX function max_weight_matching is based on Galil, Zvi (1986) [ 2 ] which employs an O(n 3 ) time algorithm.

The matching output ( odd_matching_dupes ) is a dictionary. Although there are 36 edges in this matching, you only want 18. Each edge-pair occurs twice (once with node 1 as the key and a second time with node 2 as the key of the dictionary).

You convert this dictionary to a list of tuples since you have an undirected graph and order does not matter. Removing duplicates yields the unique 18 edge-pairs that cumulatively sum to the least possible distance.

Let’s visualize these pairs on the complete graph plotted earlier in step 2.3 . As before, while the node positions reflect the true graph (trail map) here, the edge distances shown (blue lines) are as the crow flies. The actual shortest route from one node to another could involve multiple edges that twist and turn with considerably longer distance.

To illustrate how this fits in with the original graph, you plot the same min weight pairs (blue lines), but over the trail map (faded) instead of the complete graph. Again, note that the blue lines are the bushwhacking route (as the crow flies edges, not actual trails). You still have a little bit of work to do to find the edges that comprise the shortest route between each pair in Step 3.

Now you augment the original graph with the edges from the matching calculated in 2.4 . A simple function to do this is defined below which also notes that these new edges came from the augmented graph. You’ll need to know this in ** 3.** when you actually create the Eulerian circuit through the graph.

Let’s confirm that your augmented graph adds the expected number (18) of edges:

Let’s also confirm that every node now has even degree:

CPP Step 3: Compute Eulerian Circuit

Now that you have a graph with even degree the hard optimization work is over. As Euler famously postulated in 1736 with the Seven Bridges of Königsberg problem, there exists a path which visits each edge exactly once if all nodes have even degree. Carl Hierholzer fomally proved this result later in the 1870s.

There are many Eulerian circuits with the same distance that can be constructed. You can get 90% of the way there with the NetworkX eulerian_circuit function. However there are some limitations.

Limitations you will fix:

The augmented graph could (and likely will) contain edges that didn’t exist on the original graph. To get the circuit (without bushwhacking), you must break down these augmented edges into the shortest path through the edges that actually exist.

eulerian_circuit only returns the order in which we hit each node. It does not return the attributes of the edges needed to complete the circuit. This is necessary because you need to keep track of which edges have been walked already when multiple edges exist between two nodes.

Limitations you won’t fix:

• To save your legs some work, you could relax the assumption of the Eulerian circuit that one start and finish at the same node. An [Eulerian path] (the general case of the Eulerian circuit), can also be found if there are exactly two nodes of odd degree. This would save you a little bit of double backing...presuming you could get a ride back from the other end of the park. However, at the time of this writing, NetworkX does not provide a Euler Path algorithm. The [eulerian_circuit code] isn't too bad and could be adopted for this case, but you'll keep it simple here.

Nonetheless, let’s start with the simple yet incomplete solution:

As expected, the length of the naive Eulerian circuit is equal to the number of the edges in the augmented graph.

The output is just a list of tuples which represent node pairs. Note that the first node of each pair is the same as the second node from the preceding pair.

Now let’s define a function that utilizes the original graph to tell you which trails to use to get from node A to node B. Although verbose in code, this logic is actually quite simple. You simply transform the naive circuit which included edges that did not exist in the original graph to a Eulerian circuit using only edges that exist in the original graph.

You loop through each edge in the naive Eulerian circuit ( naive_euler_circuit ). Wherever you encounter an edge that does not exist in the original graph, you replace it with the sequence of edges comprising the shortest path between its nodes using the original graph.

You hack limitation 3 a bit by starting the Eulerian circuit at the far east end of the park on the Blue trail (node “b_end_east”). When actually running this thing, you could simply skip the last direction which doubles back on it.

Verbose print statements are added to convey what happens when you replace nonexistent edges from the augmented graph with the shortest path using edges that actually exist.

You see that the length of the Eulerian circuit is longer than the naive circuit, which makes sense.

CPP Solution

Here’s a printout of the solution in text:

You can tell pretty quickly that the algorithm is not very loyal to any particular trail, jumping from one to the next pretty quickly. An extension of this approach could get fancy and build in some notion of trail loyalty into the objective function to make actually running this route more manageable.

Let’s peak into your solution to see how reasonable it looks. (Not important to dwell on this verbose code, just the printed output)

Visualize CPP Solution

While NetworkX also provides functionality to visualize graphs, they are notably humble in this department:

NetworkX provides basic functionality for visualizing graphs, but its main goal is to enable graph analysis rather than perform graph visualization. In the future, graph visualization functionality may be removed from NetworkX or only available as an add-on package.

Proper graph visualization is hard, and we highly recommend that people visualize their graphs with tools dedicated to that task. Notable examples of dedicated and fully-featured graph visualization tools are Cytoscape, Gephi, Graphviz and, for LaTeX typesetting, PGF/TikZ.

That said, the built-in NetworkX drawing functionality with matplotlib is powerful enough for eyeballing and visually exploring basic graphs, so you stick with NetworkX draw for this tutorial.

I used graphviz and the dot graph description language to visualize the solution in my Python package postman_problems . Although it took some legwork to convert the NetworkX graph structure to a dot graph, it does unlock enhanced quality and control over visualizations.

Your first step is to convert the list of edges to walk in the Euler circuit into an edge list with plot-friendly attributes.

create_cpp_edgelist Creates an edge list with some additional attributes that you’ll use for plotting:

• sequence: records a sequence of when we walk each edge.
• visits: is simply the number of times we walk a particular edge.

Let’s create the CPP edge list:

As expected, your edge list has the same number of edges as the original graph.

The CPP edge list looks similar to euler_circuit , just with a few additional attributes.

Now let’s make the graph:

Here you illustrate which edges are walked once ( gray ) and more than once ( blue ). This is the "correct" version of the visualization created in 2.4 which showed the naive (as the crow flies) connections between the odd node pairs ( red ). That is corrected here by tracing the shortest path through edges that actually exist for each pair of odd degree nodes.

If the optimization is any good, these blue lines should represent the least distance possible. Specifically, the minimum distance needed to generate a matching of the odd degree nodes.

Here you plot the original graph (trail map) annotated with the sequence numbers in which we walk the trails per the CPP solution. Multiple numbers indicate trails we must double back on.

You start on the blue trail in the bottom right (0th and the 157th direction).

The movie below that traces the Euler circuit from beginning to end is embedded below. Edges are colored black the first time they are walked and red the second time.

Note that this gif doesn’t do give full visual justice to edges which overlap another or are too small to visualize properly. A more robust visualization library such as graphviz could address this by plotting splines instead of straight lines between nodes.

The code that creates it is presented below as a reference.

First a PNG image is produced for each direction (edge walked) from the CPP solution.

Then the the PNG images are stitched together to make the nice little gif above.

First the PNGs are sorted in the order from 0 to 157. Then they are stitched together using imageio at 3 frames per second to create the gif.

Congrats, you have finished this tutorial solving the Chinese Postman Problem in Python. You have covered a lot of ground in this tutorial (33.6 miles of trails to be exact). For a deeper dive into network fundamentals, you might be interested in Datacamp’s Network Analysis in Python course which provides a more thorough treatment of the core concepts.

Don’t hesitate to check out the NetworkX documentation for more on how to create, manipulate and traverse these complex networks. The docs are comprehensive with a good number of examples and a series of tutorials .

If you’re interested in solving the CPP on your own graph, I’ve packaged the functionality within this tutorial into the postman_problems Python package on Github. You can also piece together the code blocks from this tutorial with a different edge and node list, but the postman_problems package will probably get you there more quickly and cleanly.

One day I plan to implement the extensions of the CPP (Rural and Windy Postman Problem) here as well. I also have grand ambitions of writing about these extensions and experiences testing the routes out on the trails on my blog here . Another application I plan to explore and write about is incorporating lat/long coordinates to develop (or use) a mechanism to send turn-by-turn directions to my Garmin watch.

And of course one last next step: getting outside and trail running the route!

1 : Edmonds, Jack (1965). “Paths, trees, and flowers”. Canad. J. Math. 17: 449–467. 2 : Galil, Z. (1986). “Efficient algorithms for finding maximum matching in graphs”. ACM Computing Surveys. Vol. 18, No. 1: 23-38.

Chinese Postman Problem

• Reference work entry
• First Online: 01 January 2016
• Cite this reference work entry

• William R. Stewart Jr. 3  

754 Accesses

3 Altmetric

This is a preview of subscription content, log in via an institution to check access.

Access this chapter

• Available as PDF
• Read on any device
• Instant download
• Own it forever
• Available as EPUB and PDF
• Durable hardcover edition
• Dispatched in 3 to 5 business days
• Free shipping worldwide - see info

Tax calculation will be finalised at checkout

Purchases are for personal use only

Institutional subscriptions

Christofides, N. (1973). The optimal traversal of a graph. Omega, 1 , 719–732.

Article   Google Scholar  

Edmonds, J., & Johnson, E. (1973). Matching, Euler tours, and the Chinese postman problem. Mathematical Programming, 5 , 88–124.

Kwan, M. K. (1962). Graphic programming using odd or even points. Chinese Mathematics, 1 , 273–277.

Google Scholar  

Lawler, E. L., Lenstra, J. K., Rinnooy Kan, A. H. G., & Shmoys, D. B. (Eds.). (1985). The traveling salesman problem: A guided tour of combinatorial optimization . Chichester, UK: Wiley.

Download references

Author information

Authors and affiliations.

College of William and Mary, Williamsburg, VA, USA

William R. Stewart Jr.

You can also search for this author in PubMed   Google Scholar

Corresponding author

Correspondence to William R. Stewart Jr. .

Editor information

Editors and affiliations.

Robert H. Smith School of Business, University of Maryland, College Park, MD, USA

Saul I. Gass

Robert H. Smith School of Business and Institute for Systems Research, University of Maryland, College Park, MD, USA

Michael C. Fu

Rights and permissions

Reprints and permissions

Copyright information

© 2013 Springer Science+Business Media New York

About this entry

Cite this entry.

Stewart, W.R. (2013). Chinese Postman Problem. In: Gass, S.I., Fu, M.C. (eds) Encyclopedia of Operations Research and Management Science. Springer, Boston, MA. https://doi.org/10.1007/978-1-4419-1153-7_110

Download citation

DOI : https://doi.org/10.1007/978-1-4419-1153-7_110

Published : 23 January 2016

Publisher Name : Springer, Boston, MA

Print ISBN : 978-1-4419-1137-7

Online ISBN : 978-1-4419-1153-7

eBook Packages : Business and Economics

Share this entry

Anyone you share the following link with will be able to read this content:

Sorry, a shareable link is not currently available for this article.

Provided by the Springer Nature SharedIt content-sharing initiative

• Publish with us

Policies and ethics

• Find a journal
• Track your research

Chinese Postman Problem

A problem asking for the shortest tour of a graph which visits each edge at least once (Kwan 1962; Skiena 1990, p. 194). For an Eulerian graph , an Eulerian cycle is the optimal solution. In a tree , however, the path crosses each edge twice.

Explore with Wolfram|Alpha

More things to try:

• acyclic graph
• angle trisection

Referenced on Wolfram|Alpha

Cite this as:.

Weisstein, Eric W. "Chinese Postman Problem." From MathWorld --A Wolfram Web Resource. https://mathworld.wolfram.com/ChinesePostmanProblem.html

Subject classifications

6.4.4 Solving the Chinese Postman's Problem

Exercise 6.5 Prove the lemma. Hint : The sum of the degrees of all the nodes in G is an even number since each edge is incident on two nodes.

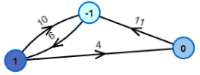
Example 7: Application of Algorithm 6.5 Consider the graph of Figure 6.15a. The numbers on the edges indicate the lengths of the edges. The graph contains four nodes of odd degree (a, b, d, and e). Thus, there are three possible matchings of the odd-degree nodes: a-b and d-e; a-d and b-e; and a-e and bad. Th e augmented networks that would result from the addition of the artificial edges corresponding to each of these three matchings are-shown in Figure 6.15b-d, respectively. Of the three matchings, the optimal is obviously the one shown in Figure 6.15c. It adds only 12 units of length to the tour as opposed to 16 for Figure 6.15b and 20 for 6.15c. Thus, the graph shown on Figure 6.15c should be the result of the procedure outlined in Steps 2 and 3 of Algorithm 6.5. Supposing that the required tour must begin at node a, a solution to the Chinese postman,s problem for the graph of Figure 6.15a is the tour {a, d, a, c, d, e, c, b, e, b, a}. Its total length is 60 units, of which 48 is the total length of the graph 6.1 5a, while 12 units are due to the artificial edges. In other words, edges (a, d) and (b, e) will be traversed twice.

In a minimum-length matching of the odd-degree nodes, no two shortest paths in the matching can have any edges in common.

From the practical point of view, this observation has two effects: 1. It eliminates from consideration a very large percentage of the possible sets of matchings that might be considered. (This percentage might be expected to increase as the number of odd-degree nodes increases.) 2. It indicates that in a minimum-length matching odd-degree nodes will be matched to other odd-degree nodes in their immediate neighborhood.

Example 8 Consider again our initial Chinese Postman problem shown in Figure 6.12. The odd-degree nodes on Figure 6.12 are C, D, F, G, I, J, K, and L. They are shown on Figure 6.17, with that part of the network model of the district that contains all the shortest paths between the odd-degree nodes. Inspection of Figure 6.17 leads to the conclusion that (although theoretically there are 7 · 5 · 3 · 1 = 105 possible sets of matchings among the eight odd-degree nodes) very few sets of matchings would even qualify for consideration. In fact, a couple of trials should be sufficient to convince the reader that the minimum-cost matching can only be the matching I-J, K-L, C-D, and F-G for a total cost (i.e., duplicated street length) of 490 units of length. The final result for the Chinese postman,s problem in this case is then shown on Figure 6.18, where edges to be traversed twice have been substituted by two edges (or pseudo-edges) each of equal length to the original one. The graph of Figure 6.18 now contains no nodes of odd degree, and thus an Euler tour can be drawn on it, beginning at any desired node and ending at the same node. The length of all Euler tours on this graph will be equal to the total length of the original graph G (3,340 units) plus the distance to be traversed twice (490 units), for a total length of 3,830 units, or about 15 percent more than the total street length of the district that the mailman is responsible for. (This turns out to be the optimum solution.)

Wolfram Demonstrations Project

Tours through a graph.

• Open in Cloud
• Download to Desktop
• Copy Resource Object

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products .

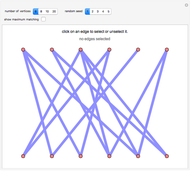
Do not show again

If we think of a graph as a road system, there are many types of optimal tours through the system that one might seek. This Demonstration shows four such tours, which can be found by various optimization methods. The starting point is shown as a larger gray disk.

Vehicle routing tour: the cycle of shortest length that visits all vertices, with repetition of edges allowed.

Traveling salesman tour: For a graph, this means the shortest Hamiltonian cycle: a cycle passing through all vertices. In one of the four cases, there is no Hamiltonian cycle.

Plotter problem route: the shortest-length route for a plotter pen that visits all edges: thus, additional straight segments where the pen is in the up position are allowed.

Chinese postman tour: the shortest-length tour that visits all edges, with repetitions allowed.

In the images, the optimal cycle starts with red edges and ends with cyan. In the Chinese postman and plotter problem cases, the vertices of odd degree are matched up in a way that minimizes the total extra distance, and that matching is indicated by colors; vertices of even degree are simply colored white.

Unchecking the "show tour" box lets you try to find the optimal cycle yourself.

Contributed by: Stan Wagon   (July 2012) (Macalester College) Open content licensed under CC BY-NC-SA

For graphs of modest size, the method of integer linear programming can be used to solve the routing problem and the traveling salesman problem. The other two problems can be solved even for graphs of very large size by using the blossom algorithm for finding a perfect matching of minimal weight.

For the plotter problem, we form the complete graph whose vertices are all odd-degree vertices, with weights being the straight-line distance between the vertices. Then a minimal-weight perfect matching of this graph tells us which edges can be added so that the resulting graph (possibly with multiple edges) has only vertices of even degree. An Eulerian tour of the resulting graph gives the optimal plotter path, since the pen-up distance is minimized.

For the Chinese postman problem, one takes a similar approach, but the weight of an edge joining two odd-degree vertices is taken to be the length of the shortest path between them in the original network. Again, the blossom algorithm can find a minimal perfect matching, and the resulting even-degree graph is Eulerian. We find an Eulerian cycle and then replace each non-edge by the corresponding shortest path in the original network.

Related Links

Permanent citation.

Stan Wagon "Tours through a Graph" http://demonstrations.wolfram.com/ToursThroughAGraph/ Wolfram Demonstrations Project Published: July 2 2012

Share Demonstration

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Topics

• Graph Theory

A classical problem in graph theory is the Eulerian Path Problem , which asks for paths or cycles that traverse all edges of a given graph exactly once. The problem was first formulated in the following form: ‘The river Pregel divides the town of Königsberg (Kaliningrad nowadays) into five parts that are connected by seven bridges. Is there a tour that passes each bridge exactly once?’

The aim of the related Chinese Postman Problem is to find a shortest path in a graph, such that this path uses each edge (directed or undirected) at least once and returns to the starting point. The most prominent example for this problem is a postman that delivers mail in some part of town and thus has to walk down every street at least once. In the Traveling Salesperson Problem the objective is to find a minimum length tour through all nodes of a graph, starting and ending at the same point.

Chinese Postman

The Chinese Postman Problem can be solved by combining the Matching Algorithms and the Hierholzer Algorithm presented above.

Hierholzer's Algorithm

The Hierholzer Algorithm computes an Eulerian Tour in a graph (if one exists).

Traveling Salesperson Problem

Try to find an optimal TSP tour yourself and compare it with an optimal solution in this little game.

Postman tour on a graph with precedence relation on arcs

• Management Information Systems

Research output : Contribution to journal › Article › peer-review

Since the introduction of the Chinese Postman Problem (CPP), many variations on the same theme have been developed. In this paper we examine still another variation. The arcs of the graph are partitioned and a precedence relation defined, specifying the order in which the elements of the partition have to be traversed. We first examine the conditions for a feasible solution to the problem. Next, we specify the graph properties of the precedence partition that insure a polynomial complexity solution of O(N 5 ), where N is the number of nodes in the original graph. When the precedence relation on sets of arcs is general, we prove that the problem of finding the minimum length of feasible postman tour is NP‐complete.

ASJC Scopus subject areas

• Information Systems
• Hardware and Architecture
• Computer Networks and Communications

Access to Document

• 10.1002/net.3230170304

Other files and links

• Link to publication in Scopus

Fingerprint

• Polynomials Engineering & Materials Science 100%

T1 - Postman tour on a graph with precedence relation on arcs

AU - Dror, Moshe

AU - Stern, Helman

AU - Trudeau, Pierre

N2 - Since the introduction of the Chinese Postman Problem (CPP), many variations on the same theme have been developed. In this paper we examine still another variation. The arcs of the graph are partitioned and a precedence relation defined, specifying the order in which the elements of the partition have to be traversed. We first examine the conditions for a feasible solution to the problem. Next, we specify the graph properties of the precedence partition that insure a polynomial complexity solution of O(N5), where N is the number of nodes in the original graph. When the precedence relation on sets of arcs is general, we prove that the problem of finding the minimum length of feasible postman tour is NP‐complete.

AB - Since the introduction of the Chinese Postman Problem (CPP), many variations on the same theme have been developed. In this paper we examine still another variation. The arcs of the graph are partitioned and a precedence relation defined, specifying the order in which the elements of the partition have to be traversed. We first examine the conditions for a feasible solution to the problem. Next, we specify the graph properties of the precedence partition that insure a polynomial complexity solution of O(N5), where N is the number of nodes in the original graph. When the precedence relation on sets of arcs is general, we prove that the problem of finding the minimum length of feasible postman tour is NP‐complete.

UR - http://www.scopus.com/inward/record.url?scp=84987039902&partnerID=8YFLogxK

UR - http://www.scopus.com/inward/citedby.url?scp=84987039902&partnerID=8YFLogxK

U2 - 10.1002/net.3230170304

DO - 10.1002/net.3230170304

M3 - Article

AN - SCOPUS:84987039902

SN - 0028-3045

JO - Networks

JF - Networks

FindPostmanTour

FindPostmanTour [ g ]

finds a Chinese postman tour in the graph g of minimal length.

FindPostmanTour [ g , k ]

finds at most k Chinese postman tours.

FindPostmanTour [ { v  w , … } , … ]

uses rules v  w to specify the graph g .

• A Chinese postman tour is a tour that traverses each edge at least once.
• FindPostmanTour returns a list of edges consisting of Chinese postman tours.
• FindPostmanTour returns the list { } if no Chinese postman tours exist.
• FindPostmanTour [ g ] is equivalent to FindPostmanTour [ g , 1 ] .
• FindPostmanTour works with undirected graphs, directed graphs, weighted graphs, and multigraphs.

Basic Examples     (2)

Find a Chinese postman tour:

Highlight the tour:

Find several Chinese postman tours:

Scope     (8)

FindPostmanTour works with undirected graphs:

Directed graphs:

Weighted graphs:

Multigraphs:

Use rules to specify the graph:

FindPostmanTour returns an empty result for a graph with no Chinese postman tours:

FindPostmanTour works with large graphs:

Applications     (3)

Find a shortest route that a newspaper carrier can use to distribute newspapers in a neighborhood:

The total distance:

Find the most efficient way for a letter carrier to deliver letters, knowing the time it takes to deliver mail on a street and the time it takes to walk a street without delivering mail (deadheading time):

A route that goes through all the streets and minimizes the total deadheading time:

Show the route:

The total delivery time:

Testing combinations of actions in a finite-state machine:

Generate a line graph:

A length-2 switch cover:

Properties & Relations     (2)

An Eulerian graph has a Chinese postman tour:

It is the same as its Eulerian cycle:

A connected graph has a Chinese postman tour:

Neat Examples     (1)

Dynamically highlight cycles:

FindEulerianCycle   FindHamiltonianCycle   FindShortestTour

Related Guides

• Paths, Cycles, and Flows
• Computation on Graphs

Introduced in 2012 (9.0) | Updated in 2014 (10.0) ▪ 2015 (10.3)

Wolfram Research (2012), FindPostmanTour, Wolfram Language function, https://reference.wolfram.com/language/ref/FindPostmanTour.html (updated 2015).

Wolfram Language. 2012. "FindPostmanTour." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2015. https://reference.wolfram.com/language/ref/FindPostmanTour.html.

Wolfram Language. (2012). FindPostmanTour. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/FindPostmanTour.html

@misc{reference.wolfram_2024_findpostmantour, author="Wolfram Research", title="{FindPostmanTour}", year="2015", howpublished="\url{https://reference.wolfram.com/language/ref/FindPostmanTour.html}", note=[Accessed: 24-April-2024 ]}

@online{reference.wolfram_2024_findpostmantour, organization={Wolfram Research}, title={FindPostmanTour}, year={2015}, url={https://reference.wolfram.com/language/ref/FindPostmanTour.html}, note=[Accessed: 24-April-2024 ]}

Enable JavaScript to interact with content and submit forms on Wolfram websites. Learn how

Forget the scale and start planning your holiday meals in Tijuana and Rosarito this winter season!

Start Planning your Dream Wedding in Ensenada

La Chinesca- A journey through Mexicali history

La Chinesca, or the Mexican Chinatown, protects the origins of a city founded on Chinese traditions, and offers visitors the opportunity to experience a fusion of two cultures in one.

Towards the end of the 19th century, there was a significant migration of Chinese people traveling to America due to political and economic changes in their country. Many arrived in Mexicali with hopes of crossing into the United States but eventually stayed in the city.

This community gradually prospered with early generations starting as workers and later becoming established merchants. The first generations settled in the city's square, where they opened up bars, restaurants, shops, and what we now know as La Chinesca.

Myths and legends exist surrounding Mexicali's Chinatown, which is connected via underground constructions and pathways. Many believe that these basements were built to help people escape the extreme climate of the region. Others point out that they were designed to separate this community from others and live undisturbed.

Underneath their shops, you find a network of tunnels leading to a hospital, smoking rooms, and even a jail. The arrival of the Free Trade Agreement (NAFTA), however, led to the bankruptcy of the two Chinescas–both underground and above–leaving this neighborhood abandoned.

The site recently opened its doors as a museum for tourists interested in learning about the ancestors and history of Mexicali. The renovation also includes murals representing historical Chinesca heroes.

Visitors visiting the Chinesca museum can descend into the basements and underground tunnels that take you on a trip back in time.

Make sure to make this a complete Mexicali itinerary by visiting one of the hundreds of famous Chinese food restaurants in the region.

Interested in taking a tour in la Chinesca?

The tours last about 1 hour and 45 minutes and can be visited from Thursday to Sunday for about 10 dollars per person. For more information, you may contact the service desk at 686 150 36 94 or send a WhatsApp message.

Related Posts

Must-see in Tijuana: The Collector’s & Lucha Libre Museum

New Years Eve Baja California’s wine region

AROUND MANDARIN ACADEMY

Come visit us.

An Unique Learning Experience in the Heart of Silicon Valley!

Mandarin Academy offers a wonderfully unique learning experience for young Chinese learners in the heart of Silicon Valley. We believe that being bilingual is one of our biggest gifts we can give to our children. Children are immersed in English in daily life at the store, in after-school activities, and in our neighborhood so to learn Mandarin, it is important that they spend many hours per school day immersed in the language. 

• About the Project
• Historical Timeline
• Presentations
• Affiliated Projects
• In the News
• Events & News

Arboretum Chinese Labor Quarters

A collaborative, community-based archaeology project about the history of Chinese workers at Stanford

Discovery: Science and History Work Together

The Arboretum Chinese Labor Quarters site (ACLQ) is located in the Stanford University Arboretum. The site housed Chinese employees who worked across Stanford lands. They were instrumental in the creation and maintenance of the University’s iconic historic landscapes: the Arboretum, Palm Drive, the Oval, and the gardens of the Main Quadrangle. The site was occupied between the 1880s and 1925 when the last resident left and the buildings were demolished.

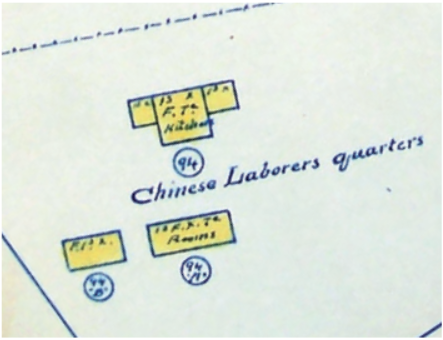
During spring 2017, work within the project grid located a trash midden, likely associated with the Quarters’ kitchen. Archaeologists hand excavated a small trench through the midden, recovering Chinese ceramics and food remains that were typical of Chinese-style meals. The discovery of the ACLQ site shows how the study of historical documents, when combined with scientific survey methodology, can aid in locating of archaeological sites whose locations have been lost to time.

A gardener working in the grounds of the Stanford’s Palo Alto residence

Opportunity for Research, Education, and Engagement

The ACLQ presents a unique and important opportunity to engage scholars, students, and members of the Chinese American community to partner in studying the important role of Chinese employees in the founding and operating of Stanford University. Research at the ACLQ also contributes to important themes in the history of the American West and U.S.- China relations.

virtual exhibit

Chinese american at stanford: a reflexive archaeology.

This student-curated exhibit produced by Bright Zhou (Class of 2016) during an independent study course taught by Christina J. Hodge presents evocative items excavated from the Arboretum Chinese Labor Quarters site and the Stanford Mansion on campus lands.

University Archives

Topic guide.

The University Archives is proud to collaborate with the Stanford Archeology Center, Heritage Services, and the Arboretum Chinese Labor Quarters Project in an effort to document and share with the public primary sources relating to early Chinese and Chinese Americans at Stanford.

To that end, we have created a Topic Guide to our collections, which include various records from Leland Stanford’s Palo Alto Stock Farm, scrapbooks, photographs, diaries, and maps. All of these materials are available for research use by the general public. Although no appointment is necessary for visiting, our materials are stored offsite so please order materials ahead of your visit.

For more information on visiting us and using our collections please visit https://library.stanford.edu/spc/using-our-collections .

Image provided by the Stanford University Libraries

Barbara L. Voss (on Sabbatical September 2020 – August 2021)

Associate professor, department of anthropology faculty advisor, arboretum chinese labor quarters project [email protected].

I am a historical archaeologist who studies transnational cultural encounters. My research on 19th century migration from southern China includes the Market Street Chinatown Archaeology Project in San Jose, California; the Chinese Railroad Workers in North America Project; and the Cangdong Village Archaeology Project in Guangdong Province. On the Arboretum Chinese Labor Quarters Project, I provide academic mentoring, coordinate research partnerships, and participate in heritage stakeholder consultation.

Christina J. Hodge

Academic curator and collections manager, stanford university archaeology collections [email protected].

I am a museum anthropologist and historical archaeologist engaged in decolonizing museum practices and social archaeologies of colonial America. I lead the Stanford University Archaeology Collections, a museum quality collection of artifacts from around the world, including from campus lands. SUAC will be the permanent home for the material finds and documentary archive from the Arboretum Chinese Labor Quarters Project. I currently serve an advisory and logistical role relating to the documentation and care of ACLQ collections.

Heritage Services

We are a team of Stanford staff archaeologists and historians managing the Asian American Heritage Survey effort and providing support in archival research, mapping, data recovery, and collections processing for the Arboretum Chinese Labor Quarters project. We work towards evaluating and preserving the heritage of Stanford campus and the surrounding lands.

Dylan Bergersen, Archaeology Technician

Julie Cain, Historian & Historic Preservation Planner

Lauren Conway, Heritage Program Coordinator, [email protected]

Laura Jones, University Archaeologist and Director , Heritage Services [email protected]

Koji Lau-Ozawa, Archaeologist, PhD candidate

Shane Martin, Archaeology Technician

Carol Porter, Heritage Data Systems & Facilities Coordinator

Marco Ramos Barajas, Archaeology Technician

Katrinka Reinhart, Archaeologist

Garrett Trask, Staff Archaeologist, [email protected]

Suzanne Ubick, Archaeologist

Affiliated Researchers

Megan R. Victor, Queens’ College, City University of New York, [email protected]

J. Ryan Kennedy, University of New Orleans

Virginia Popper, University of Massachusetts, Boston

Veronica Peterson, Harvard University

If you would like to find out more or receive project updates, please subscribe to our mailing list or contact us through social media @ACLQProject. We look forward to hearing from you!

© 2018 Arboretum Chinese Labor Quarters

And those big premieres are still being held at the Chinese on a regular basis. If you would like to watch the stars arrive in person on the red carpet at these premieres, just see my Calendar of Events page for the dates and times of upcoming premieres. Then show up early and wait (hint: wear comfortable shoes.)

It's been featured on TV sitcoms as well - remember the episode of " I Love Lucy " where Lucy stole the cement block bearing John Wayne 's footprints? Or how about the episode of " The Beverly Hillbillies " where Jed and Jethro thought that the forecourt had been vandalized by the stars, and were caught trying to pave over the "evidence " with wet cement!

For a while, the theatre was renamed " Mann's Chinese Theatre" after it was purchased by Ted Mann in 1973, the owner of the Mann's Theatre chain (and husband of actress Rhonda Fleming ). But fortunately, the landmark later regained its original name.

Outside, near the forecourt, you'll find that the fist business is thriving, with several booths set up hawking various guided bus tours of Hollywood, the movie stars' homes, and greater L.A. Two theatre gift shops offer the usual selection of touristy Tinseltown souvenirs, at outrageous prices. And it isn't unusual to see street performers (such as a Charlie Chaplin look-alike) milling with the crowd of tourists on the fabled forecourt.

And of course, for the price of a movie ticket, you can go inside and see the theatre's well-preserved interior as well.

You might suspect that after seven decades, the theatre's interior would be dilapidated, like many of the other older theatres in L.A. But in fact, the Chinese Theatre remains in surprisingly good condition. Its interior decor is a dazzling blur of exotic Asian motifs.

The lobby boasts elaborate wall murals depicting life in the Orient, bold red and gold columns, and a colossal, intricate Chinese chandelier. In the lobby's west wing is a glass case containing three wax figures (from the Hollywood Wax Museum ) wearing authentic Chinese costumes from Cathay. The three female figures surround a now-empty chair that once held the wax likeness of actress Rhonda Fleming , wife of owner Ted Mann. Movie-makers used to consider it good luck to come to the theatre and touch these wax figures before embarking on a new film project.

Inside the vast auditorium , the 2,200 bright red seats and red carpeting are kept clean and in excellent condition. Overhead, a spectacular chandelier illuminates the center of a mammoth, ornate starburst, surrounded by a ring of dragons - which is, in turn, encircled by a ring of icons portraying scenes from Chinese drama. Smaller Oriental lamps glow at the sides of the auditorium, hanging between intricately-carved stone columns; black & white murals of trees and pagodas fill the spaces in between.

Turn around and look behind you in the theatre, and you'll discover that what would usually have been the balcony section was divided into four private opera boxes for visiting celebrities. Also, note the large number of assorted Asian statues, gongs, vases, shields, and friezes employed to add to the theatre's overall exotic ambiance. (My only complaint is that the interior lighting is kept so dim that it is difficult to appreciate all of the theatre's lavish detail.)

The Chinese Theatre may not be the best-preserved theatre in Hollywood - that honor would go to Disney's recently-restored El Capitan , across the street - but it is certainly in fine condition for a 70-year-old movie palace. And they've kept up with the times when it comes to movie technology, too: the theatre offers 70mm projection and a state-of-the-art THX sound system (which can actually be a little too loud at times).

But whether you plan to see a movie here or not, if you're going to make the pilgrimage to Hollywood, the Chinese Theatre is a must-see.

The famous courtyard is open free of charge to all visitors. You do not have to buy a ticket to a movie to view the forecourt and its footprints.

But the biggest news is that the Hollywood & Highland project opened right next door to Grauman's Chinese. In fact, the spectacular development takes up the entire block, from Orange to Highland, and essentially surrounds the historic theatre. The $600 million project includes the permanent home for the Academy Awards show (the Dolby Theatre), a grand ballroom for post-Oscar parties, restaurants, nightclubs, retail shops, a luxury hotel and parking for 3,000 cars. Six smaller, modern cinemas have been built next door (to the east of the existing theatre), and the main Chinese theatre has undergone a major renovation, removing the box office and some of the more recent signs, to return the theatre to the way it looked when it first opened.

Update : In 2013, they sold the naming rights of the theatre, and as a result, the official name is now "TCL Chinese Theatre", named after the Chinese electronics company that paid $5 million for the right to slap their name on the marquee.  Of course, it will always be called Grauman's Chinese by the public.  Trying to rename something as well-known and historic as Grauman's Chinese is like trying to rename the Eiffel Tower.  You might convince the media to play along, but the public knows better.

On the bright side, the current owners (producer Donald Kushner & Elie Samaha) used some of that money to turn the interior of Grauman's into the largest IMAX theatre in the world (in terms of seating capacity) with 986 tiered seats and a 94-foot wide screen.  They promised to leave the historic elements of the theatre interior intact, but they hope that the new IMAX screen will allow the theatre to host even more movie premieres than usual (as well as providing a more comfortable, modern viewing experience for the audience).  The theatre was be closed briefly, from May until September 2013, but is now open again with its new IMAX screen.

Parking : Parking can be a real problem on Hollywood Blvd. There is some limited free street parking on the residential streets just south of the boulevard, such as Hawthorne. There is a one-hour limit on these streets, but not if you visit on Sunday. Parking is now available in the garage under the new Hollywood & Highland project (be sure to get your parking ticket validated, for a reduced fee) - enter on Orange Ave. There are also paid lots south of Hollywood Blvd (and east of Orange), and there is a paid parking lot on the west side of Highland, just south of Hollywood Boulevard.

(The outdoor courtyard is open 24 hours a day, but use common sense and come at a sensible hour.) Also see the separate pages about the Chinese theatre forecourt , and the installation ceremonies where you can see the stars put their footprints in cement.

[For more information about the theatre, you can access Grauman's official website at: http://www.tclchinesetheatres.com/ .]

Looking for something in particular? Search the Seeing-Stars website!