travelling salesperson problem using dynamic programming

• Data Structures & Algorithms
• DSA - Overview
• DSA - Environment Setup
• DSA - Algorithms Basics
• DSA - Asymptotic Analysis
• Data Structures
• DSA - Data Structure Basics
• DSA - Data Structures and Types
• DSA - Array Data Structure
• Linked Lists
• DSA - Linked List Data Structure
• DSA - Doubly Linked List Data Structure
• DSA - Circular Linked List Data Structure
• Stack & Queue
• DSA - Stack Data Structure
• DSA - Expression Parsing
• DSA - Queue Data Structure
• Searching Algorithms
• DSA - Searching Algorithms
• DSA - Linear Search Algorithm
• DSA - Binary Search Algorithm
• DSA - Interpolation Search
• DSA - Jump Search Algorithm
• DSA - Exponential Search
• DSA - Fibonacci Search
• DSA - Sublist Search
• DSA - Hash Table
• Sorting Algorithms
• DSA - Sorting Algorithms
• DSA - Bubble Sort Algorithm
• DSA - Insertion Sort Algorithm
• DSA - Selection Sort Algorithm
• DSA - Merge Sort Algorithm
• DSA - Shell Sort Algorithm
• DSA - Heap Sort
• DSA - Bucket Sort Algorithm
• DSA - Counting Sort Algorithm
• DSA - Radix Sort Algorithm
• DSA - Quick Sort Algorithm
• Graph Data Structure
• DSA - Graph Data Structure
• DSA - Depth First Traversal
• DSA - Breadth First Traversal
• DSA - Spanning Tree
• Tree Data Structure
• DSA - Tree Data Structure
• DSA - Tree Traversal
• DSA - Binary Search Tree
• DSA - AVL Tree
• DSA - Red Black Trees
• DSA - B Trees
• DSA - B+ Trees
• DSA - Splay Trees
• DSA - Tries
• DSA - Heap Data Structure
• DSA - Recursion Algorithms
• DSA - Tower of Hanoi Using Recursion
• DSA - Fibonacci Series Using Recursion
• Divide and Conquer
• DSA - Divide and Conquer
• DSA - Max-Min Problem
• DSA - Strassen's Matrix Multiplication
• DSA - Karatsuba Algorithm
• Greedy Algorithms
• DSA - Greedy Algorithms
• DSA - Travelling Salesman Problem (Greedy Approach)
• DSA - Prim's Minimal Spanning Tree
• DSA - Kruskal's Minimal Spanning Tree
• DSA - Dijkstra's Shortest Path Algorithm
• DSA - Map Colouring Algorithm
• DSA - Fractional Knapsack Problem
• DSA - Job Sequencing with Deadline
• DSA - Optimal Merge Pattern Algorithm
• Dynamic Programming
• DSA - Dynamic Programming
• DSA - Matrix Chain Multiplication
• DSA - Floyd Warshall Algorithm
• DSA - 0-1 Knapsack Problem
• DSA - Longest Common Subsequence Algorithm
• DSA - Travelling Salesman Problem (Dynamic Approach)
• Approximation Algorithms
• DSA - Approximation Algorithms
• DSA - Vertex Cover Algorithm
• DSA - Set Cover Problem
• DSA - Travelling Salesman Problem (Approximation Approach)
• Randomized Algorithms
• DSA - Randomized Algorithms
• DSA - Randomized Quick Sort Algorithm
• DSA - Karger’s Minimum Cut Algorithm
• DSA - Fisher-Yates Shuffle Algorithm
• DSA Useful Resources
• DSA - Questions and Answers
• DSA - Quick Guide
• DSA - Useful Resources
• DSA - Discussion
• Selected Reading
• UPSC IAS Exams Notes
• Developer's Best Practices
• Questions and Answers
• Effective Resume Writing
• HR Interview Questions
• Computer Glossary

Travelling Salesman Problem (Dynamic Approach)

Travelling salesman dynamic programming algorithm, implementation.

Travelling salesman problem is the most notorious computational problem. We can use brute-force approach to evaluate every possible tour and select the best one. For n number of vertices in a graph, there are (n−1)! number of possibilities. Thus, maintaining a higher complexity.

However, instead of using brute-force, using the dynamic programming approach will obtain the solution in lesser time, though there is no polynomial time algorithm.

Let us consider a graph G = (V,E) , where V is a set of cities and E is a set of weighted edges. An edge e(u, v) represents that vertices u and v are connected. Distance between vertex u and v is d(u, v) , which should be non-negative.

Suppose we have started at city 1 and after visiting some cities now we are in city j . Hence, this is a partial tour. We certainly need to know j , since this will determine which cities are most convenient to visit next. We also need to know all the cities visited so far, so that we don't repeat any of them. Hence, this is an appropriate sub-problem.

For a subset of cities S $\epsilon$ {1,2,3,...,n} that includes 1 , and j $\epsilon$ S, let C(S, j) be the length of the shortest path visiting each node in S exactly once, starting at 1 and ending at j .

When |S|> 1 , we define 𝑪 C(S,1)= $\propto$ since the path cannot start and end at 1.

Now, let express C(S, j) in terms of smaller sub-problems. We need to start at 1 and end at j . We should select the next city in such a way that

$$C\left ( S,j \right )\, =\, min\, C\left ( S\, -\, \left\{j \right\},i \right )\, +\, d\left ( i,j \right )\: where\: i\: \epsilon \: S\: and\: i\neq j$$

There are at the most 2 n .n sub-problems and each one takes linear time to solve. Therefore, the total running time is O(2 n .n 2 ) .

In the following example, we will illustrate the steps to solve the travelling salesman problem.

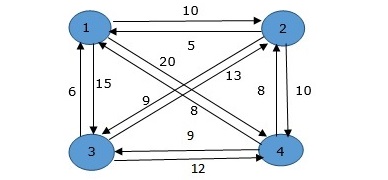
From the above graph, the following table is prepared.

$$Cost\left ( 2,\Phi ,1 \right )\, =\, d\left ( 2,1 \right )\,=\,5$$

$$Cost\left ( 3,\Phi ,1 \right )\, =\, d\left ( 3,1 \right )\, =\, 6$$

$$Cost\left ( 4,\Phi ,1 \right )\, =\, d\left ( 4,1 \right )\, =\, 8$$

$$Cost(i,s)=min\left\{Cos\left ( j,s-(j) \right )\, +\,d\left [ i,j \right ] \right\}$$

$$Cost(2,\left\{3 \right\},1)=d[2,3]\, +\, Cost\left ( 3,\Phi ,1 \right )\, =\, 9\, +\, 6\, =\, 15$$

$$Cost(2,\left\{4 \right\},1)=d[2,4]\, +\, Cost\left ( 4,\Phi ,1 \right )\, =\, 10\, +\, 8\, =\, 18$$

$$Cost(3,\left\{2 \right\},1)=d[3,2]\, +\, Cost\left ( 2,\Phi ,1 \right )\, =\, 13\, +\, 5\, =\, 18$$

$$Cost(3,\left\{4 \right\},1)=d[3,4]\, +\, Cost\left ( 4,\Phi ,1 \right )\, =\, 12\, +\, 8\, =\, 20$$

$$Cost(4,\left\{3 \right\},1)=d[4,3]\, +\, Cost\left ( 3,\Phi ,1 \right )\, =\, 9\, +\, 6\, =\, 15$$

$$Cost(4,\left\{2 \right\},1)=d[4,2]\, +\, Cost\left ( 2,\Phi ,1 \right )\, =\, 8\, +\, 5\, =\, 13$$

$$Cost(2,\left\{3,4 \right\},1)=min\left\{\begin{matrix} d\left [ 2,3 \right ]\,+ \,Cost\left ( 3,\left\{ 4\right\},1 \right )\, =\, 9\, +\, 20\, =\, 29 \\ d\left [ 2,4 \right ]\,+ \,Cost\left ( 4,\left\{ 3\right\},1 \right )\, =\, 10\, +\, 15\, =\, 25 \\ \end{matrix}\right.\, =\,25$$

$$Cost(3,\left\{2,4 \right\},1)=min\left\{\begin{matrix} d\left [ 3,2 \right ]\,+ \,Cost\left ( 2,\left\{ 4\right\},1 \right )\, =\, 13\, +\, 18\, =\, 31 \\ d\left [ 3,4 \right ]\,+ \,Cost\left ( 4,\left\{ 2\right\},1 \right )\, =\, 12\, +\, 13\, =\, 25 \\ \end{matrix}\right.\, =\,25$$

$$Cost(4,\left\{2,3 \right\},1)=min\left\{\begin{matrix} d\left [ 4,2 \right ]\,+ \,Cost\left ( 2,\left\{ 3\right\},1 \right )\, =\, 8\, +\, 15\, =\, 23 \\ d\left [ 4,3 \right ]\,+ \,Cost\left ( 3,\left\{ 2\right\},1 \right )\, =\, 9\, +\, 18\, =\, 27 \\ \end{matrix}\right.\, =\,23$$

$$Cost(1,\left\{2,3,4 \right\},1)=min\left\{\begin{matrix} d\left [ 1,2 \right ]\,+ \,Cost\left ( 2,\left\{ 3,4\right\},1 \right )\, =\, 10\, +\, 25\, =\, 35 \\ d\left [ 1,3 \right ]\,+ \,Cost\left ( 3,\left\{ 2,4\right\},1 \right )\, =\, 15\, +\, 25\, =\, 40 \\ d\left [ 1,4 \right ]\,+ \,Cost\left ( 4,\left\{ 2,3\right\},1 \right )\, =\, 20\, +\, 23\, =\, 43 \\ \end{matrix}\right.\, =\, 35$$

The minimum cost path is 35.

Start from cost {1, {2, 3, 4}, 1}, we get the minimum value for d [1, 2]. When s = 3, select the path from 1 to 2 (cost is 10) then go backwards. When s = 2, we get the minimum value for d [4, 2]. Select the path from 2 to 4 (cost is 10) then go backwards.

When s = 1, we get the minimum value for d [4, 2] but 2 and 4 is already selected. Therefore, we select d [4, 3] (two possible values are 15 for d [2, 3] and d [4, 3], but our last node of the path is 4). Select path 4 to 3 (cost is 9), then go to s = ϕ step. We get the minimum value for d [3, 1] (cost is 6).

Following are the implementations of the above approach in various programming languages −

• [email protected]

What’s New ?

The Top 10 favtutor Features You Might Have Overlooked

• Don’t have an account Yet? Sign Up

Remember me Forgot your password?

• Already have an Account? Sign In

Lost your password? Please enter your email address. You will receive a link to create a new password.

Back to log-in

By Signing up for Favtutor, you agree to our Terms of Service & Privacy Policy.

Travelling Salesman Problem using Dynamic Programming

• Jun 17, 2023
• 7 Minutes Read
• Why Trust Us We uphold a strict editorial policy that emphasizes factual accuracy, relevance, and impartiality. Our content is crafted by top technical writers with deep knowledge in the fields of computer science and data science, ensuring each piece is meticulously reviewed by a team of seasoned editors to guarantee compliance with the highest standards in educational content creation and publishing.
• By Harshita Rajput

Imagine you have to go to a party in another city and return back home as soon as possible. Which algorithm will you apply to reach your home so that you cover the shortest distance? Let us understand Travelling Salesman Problem in this guide.

What is Traveling Salesman Problem?

The Traveling Salesman Problem classic optimization problem in Computer Science. There is a salesman who wants to travel over a number of cities and he has to return back to the original city he started from and he has the choice to start from any of the cities he wants to. During his journey, we need to minimize the total distance traveled by him. 

Here is the main problem statement:

" We will be given a graph that will be represented in the form of an adjacency matrix, say distance, that denotes the distance between 2 cities, say, i and j. The distance[i][j] denotes the distance between 2 cities if the value of dist[i][j] == 0; this implies the given cities are not connected i.e. no direct edge exists between them. We can start from any node and we need to return to the original city through the shortest distance covering all the cities. "

So, basically, we need to complete a cycle in this question, and such a cycle is known as the Hamiltonian cycle. A Hamiltonian cycle is a set of edges such that every node is visited only once and we come back to the original position. So in short, in this problem, we need to return a minimum weight Hamiltonian cycle. We just have to minimize the total cost of the cycle.

Let's first try to get a Hamiltonian cycle with minimum weight from the graph below. Given the following graph and the distance between cities he has traveled, let's find out the shortest path in which he can travel all the cities.

The Hamiltonian cycle with min weight can be:

How does the Algorithm Work?

Let's take an example of a graph say:

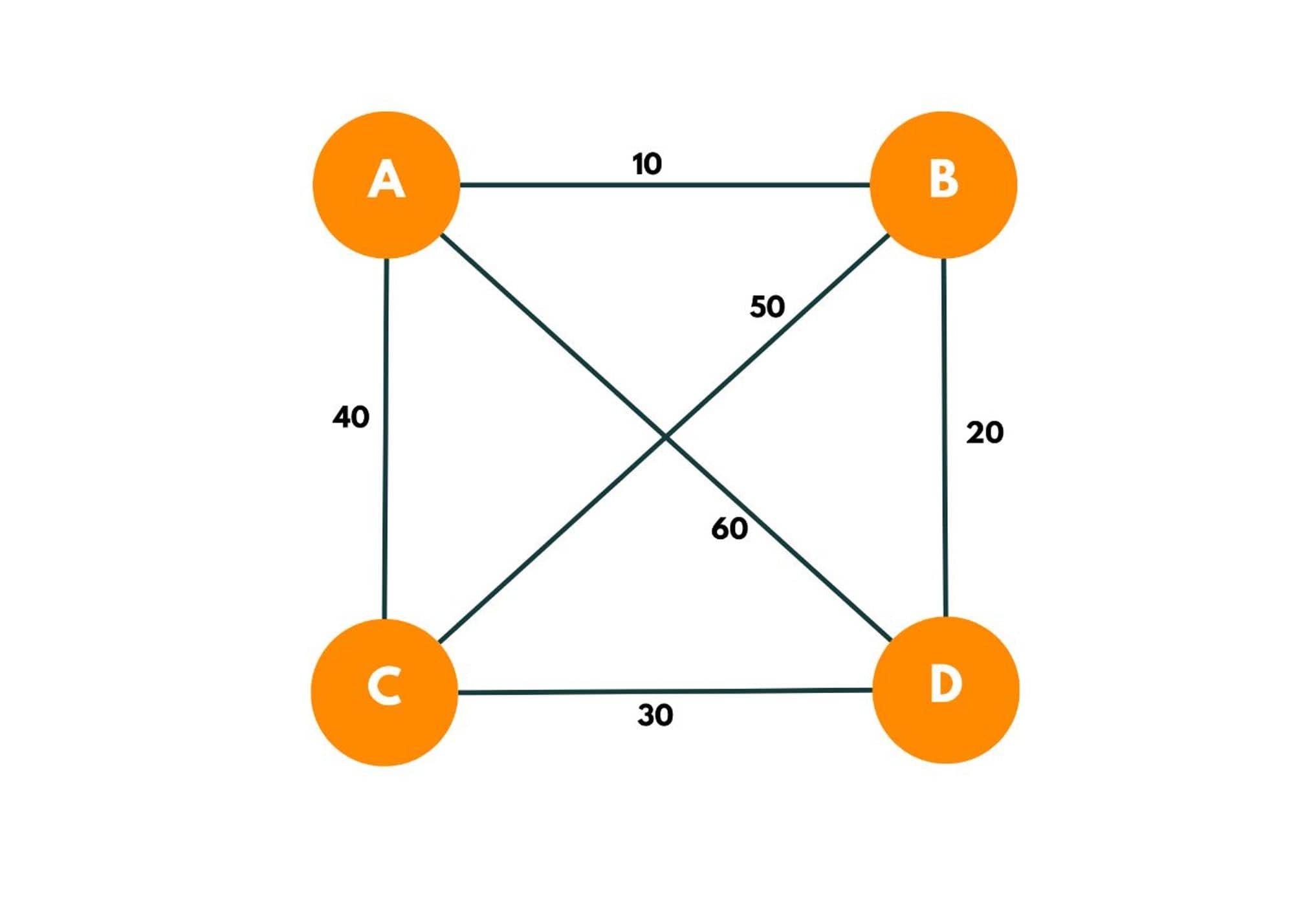
• As we have an option to start from any position, we start from A.
• Making a recursion tree and using bit masking. 

As 4 cities are there, the bit mask here would be = 0000 (at the beginning) respectively denoting D, C, B, and A  cities. The bit shows 0 for a particular city if it has not been visited and 1 if already been visited. So if bit mask = 1111 that means all bits are set, which implies all cities have been visited and we can denote this by 1<

We try to find the possible options that exist. This can be done by iterating over the adjacency matrix of A or the other way of doing so can be iterating over other cities and checking if they can be a possible option to travel from A. As we begin, we visit city A, and the bit mask value is now changed to 0001.

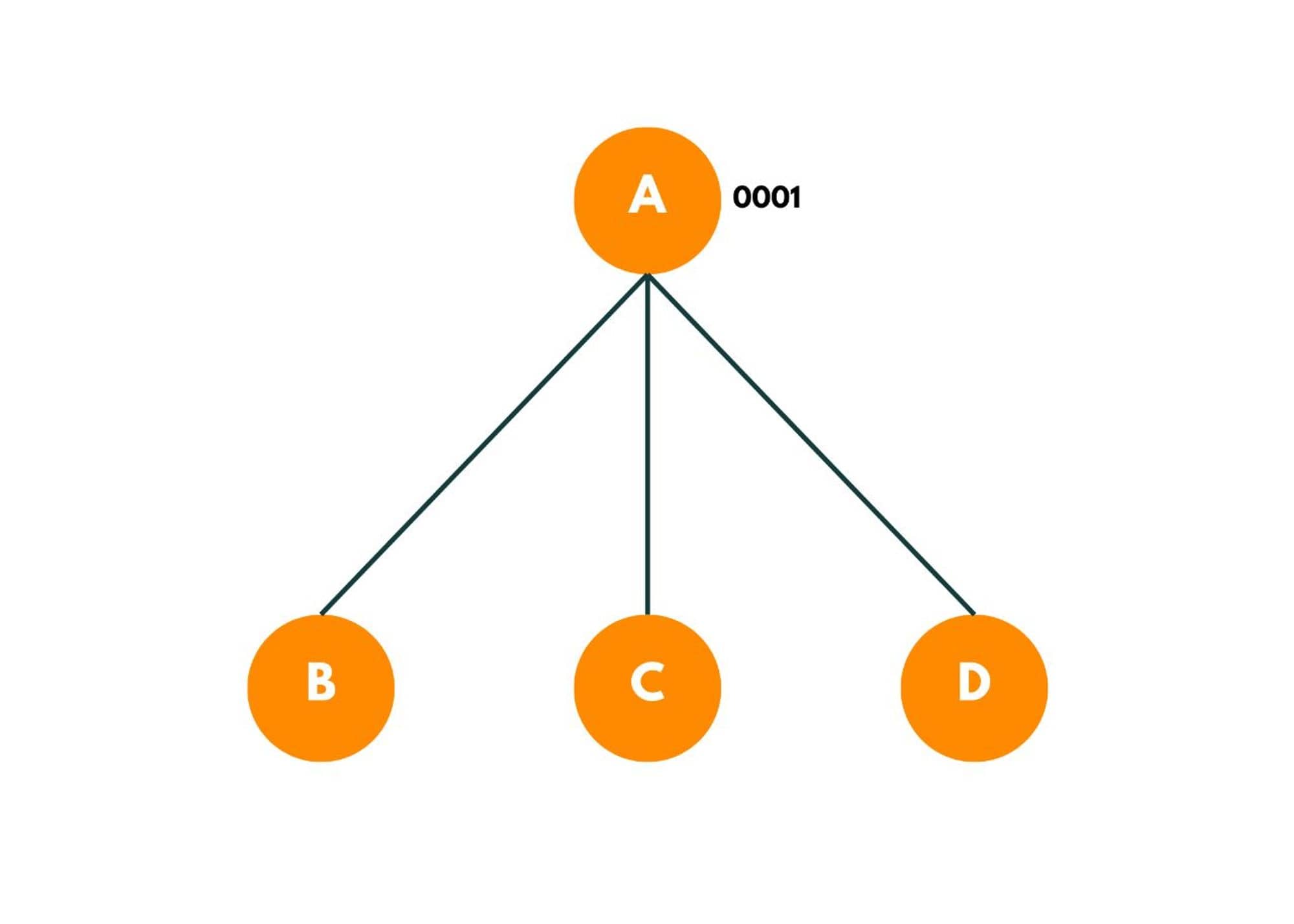
Each of these recursive branches denotes one path.

Now, as we move forward from A to B, we add the distance in a variable, say, ans. And we mark city B as visited.

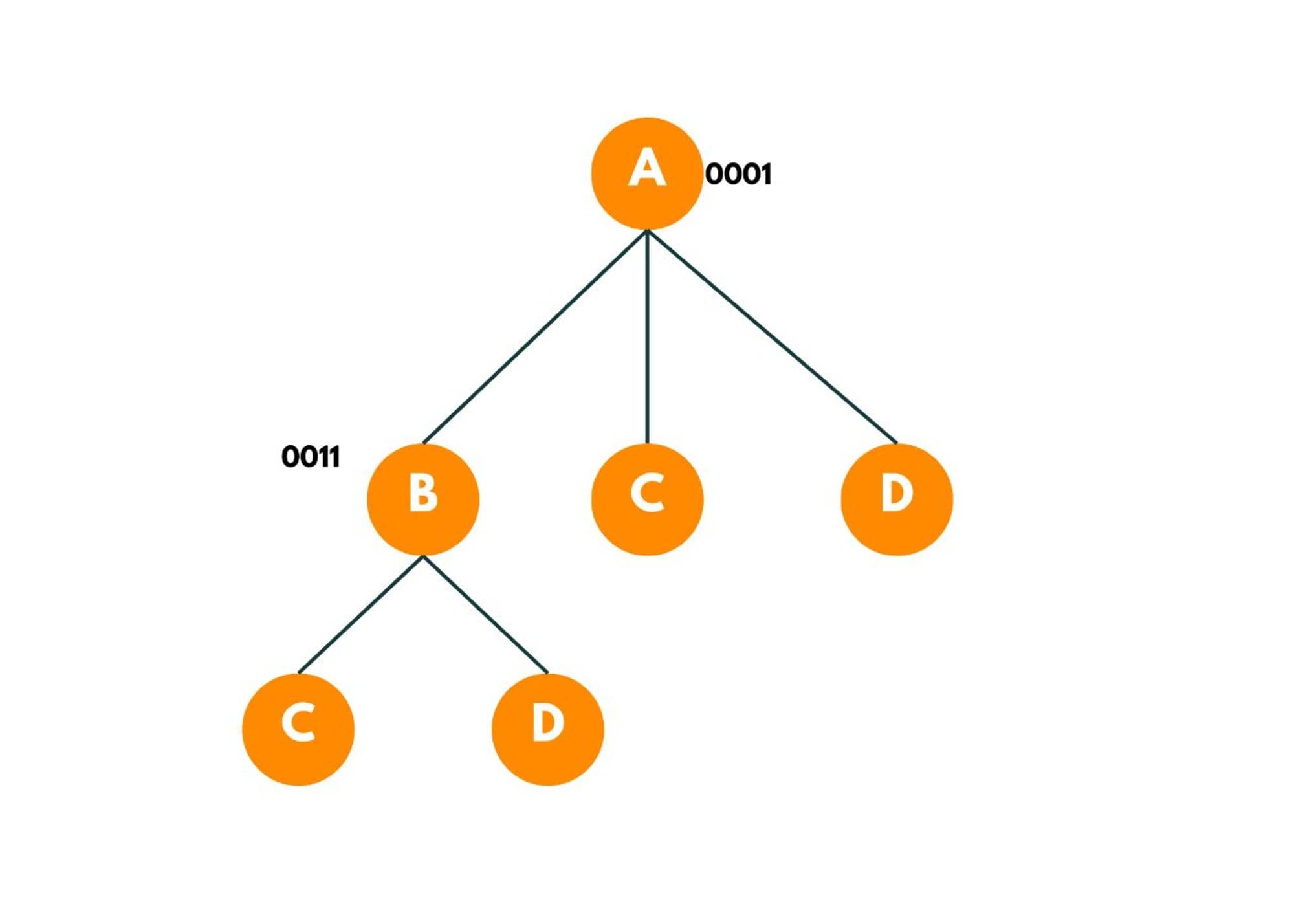
We add the distance to the answer. Now we only visit the cities from B that aren't visited yet so we have 2 options available C and D.

We then move to C and then to D while marking them visited and adding the cost to the and. Now here, we have explored each unvisited city. So now we backtrack, while marking each city as unvisited and go to the original city if a direct edge between them exists. As there is a direct edge from D to A and C to A, the nodes return the cost required to go back to the original source.

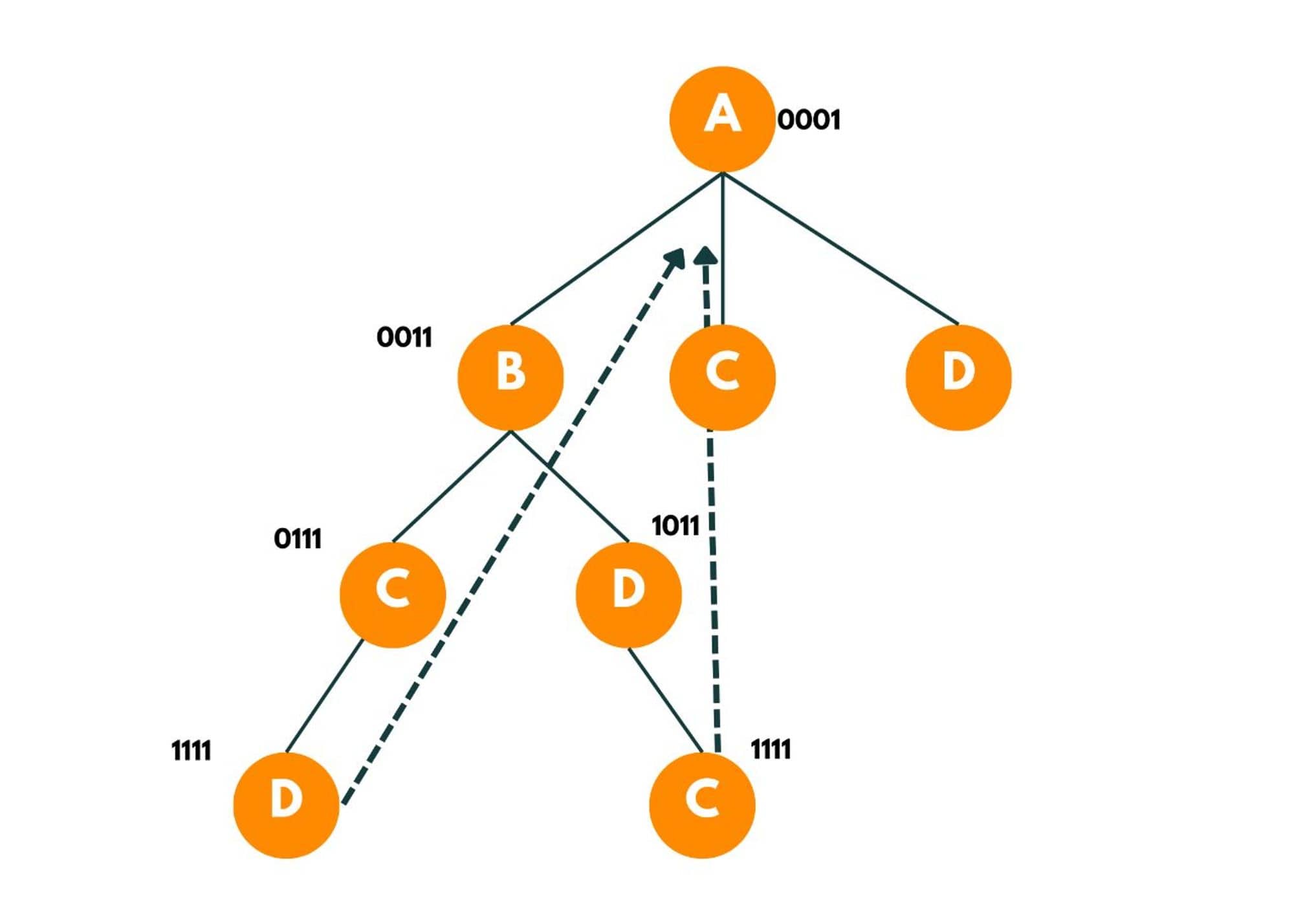
This way we explore each available option from the starting node. We also maintain a minimum cost variable that maintains the minimum cost spent to visit each city and return to the original city.

The recursion tree would look like this:

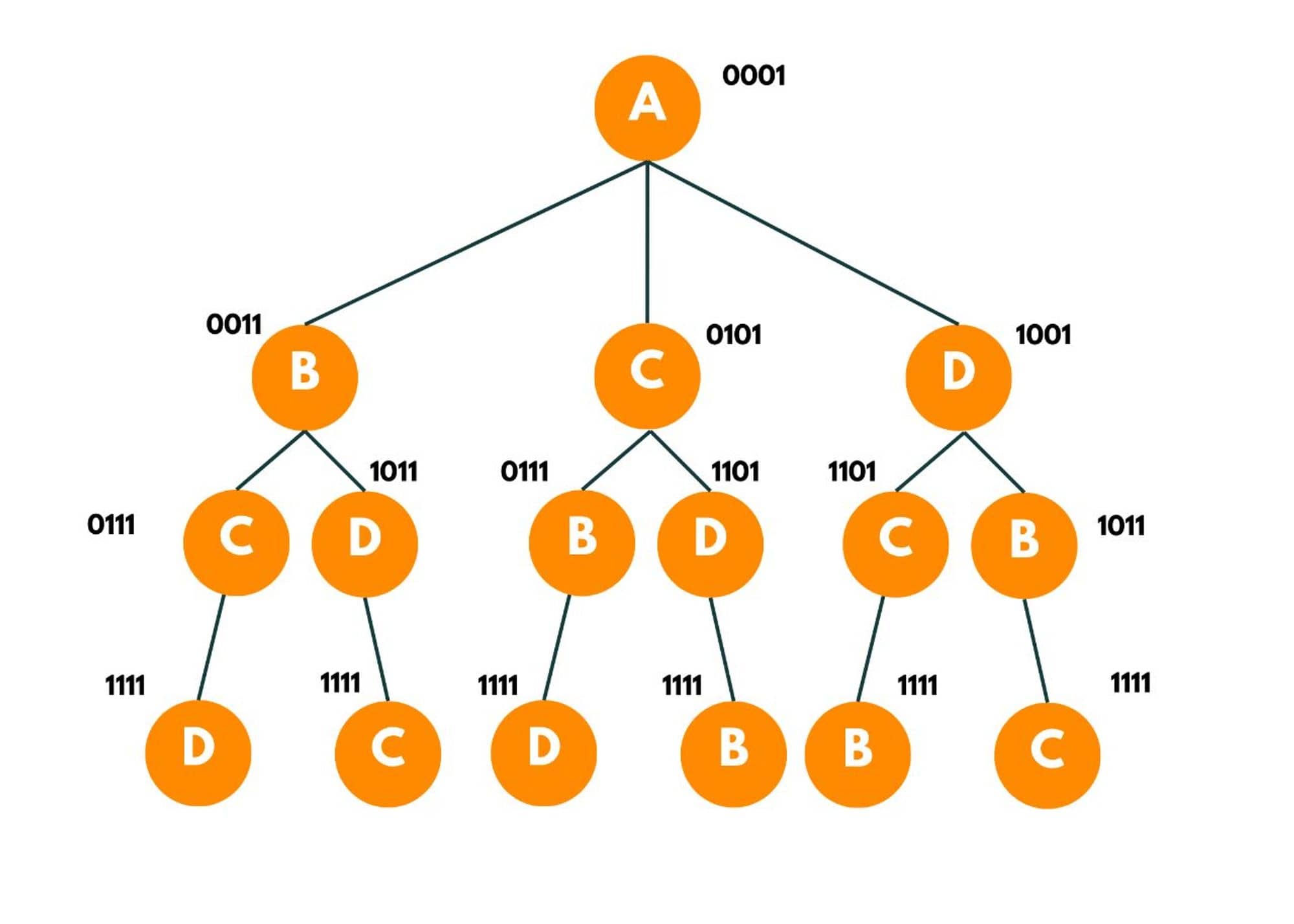
Traveling Salesman Algorithm

Here is the algorithm for Travelling Salesman Problem:

• Define the mask as (1<<n)-1.
• Create a function, say, tsp() having mask and city as arguments. As the mask denotes a set of cities visited so far, we iterate over the mask and get to know which city isn't visited.
• The base case is when we visit all the cities i.e. mask has all of its bits set, we return the distance between the current city and the original city.
• If the city is not visited, we make recursive calls by adding the distance of the original city and the city not visited and try to get the distance remaining from recursive calls
• In the recursive call, we pass a mask with the current city visited and the current city.

Travelling Salesman Problem in Java

Here is the complete Java Program to implement Travelling Salesman Problem:

Time & Space Complexity 

Here we have fixed the source node as we get the same answer whether we start from A or B or any other node because of that cyclic permutation in this case.

The time complexity of the Travelling Salesman Problem comes out to be O(n-1!). The space complexity of this code comes out to be O(n).

Now we can notice that this bitmask can only have 2^n values ranging from 0000 to 1111. The city can take n values. So the total number of distinct states comes out to be (2^n )* n. Also in this approach, some sub-problems were getting overlapped.

To optimize this approach, we use DP. We will create a 2D DP table of the values and we memorize all the results for the given value of mask and city.

Optimized Approach using Dynamic Programming

Here is the simple way to implement the Optimized Approach using Dynamic Programming. Initially we make a 2D array of [2^n][n] and initially put -1 at each position as initially, all states have values = -1.

To avoid overlapping subproblems i.e. avoiding a state which has already been computed, we check dp[bitMask][city]. If this comes out to be -1, implies the city hasn't been visited, else the city has already been visited and we return dp[bitMask][city] = ans.

Here is the Java Code for Travelling Salesman Problem using Dynamic Programming:

The time complexity comes out to be O(n ^2 * (2*n)). As we are using an extra space of (2^n) *n. The space complexity comes out to be O((2^n) *n).

Conclusion 

Travelling Salesman is a classic problem demanding in-depth knowledge of graphs and DP. It is an NP-hard problem. The optimization used in this problem can be implemented in other questions of this type too. This problem is necessary from the interview point of view, so I hope you all understood it well!

FavTutor - 24x7 Live Coding Help from Expert Tutors!

About The Author

Harshita Rajput

More by favtutor blogs, paired sample t-test using r (with examples), aarthi juryala.

MANOVA Test using R: Multivariate Analysis of Variance

Removing Scientific Notations in R (3 Easy Methods)

Travelling Salesperson Problem using Dynamic Approach in C++

In this tutorial, we will learn about the TSP(Travelling Salesperson problem) problem in C++. In this tutorial, we will learn about what is TSP. Next, what are the ways there to solve it and at last we will solve with the C++, using Dynamic Approach. This is also known as Travelling Salesman Problem in C++.

Let’s take a scenario. Suppose you want to travel by car from your home to 4 places and at the end of it you want to return back to your home. Taking the problem as a worst case, let’s think all the 4 places are connected with each other [we are taking the worst case because we don’t know in details about the places ].

TSP USING DYNAMIC APPROACH in C++

To solve the problem we have some exact conditions :

•      You can only visit each place only once. Once visited you can’t visit the place.
•       Most importantly you have to find the shortest path. [This condition will differentiate the problem with Hamiltonian Problem.

We know what are the conditions we have to follow. Now we are going to see what are the process we can use in this problem.

Approaches to solve TSP :

•      Dynamic Approach
•      Brute Force Approach
•      Backtracking Approach
•      Branch and Bound
•      Genetic Algorithm
•      Simulated Annealing

– We are not going to use every approach to solve the problem. We are going to pick up the Dynamic Approach to solve the problem.

Now the question is why Dynamic approach?

Brute Force (or we can tell Backtracking Approach ) solves the problem, checking all the possible solutions to solve it. That will take O(n^n) time to solve it. But in the Dynamic Approach, we can divide the problem into subproblems.

Let’s check the coding of TSP using Dynamic Approach.

Travelling Salesperson Problem in C++

Time Complexity :

Thus we have learned How to solve Travelling Salesperson Problem in C++.

Put your doubts and questions in the below comment section.

You may also learn:

• Activity Selection Problem using Greedy method in C++

4 responses to “Travelling Salesperson Problem using Dynamic Approach in C++”

Thanks A lot !! alert(“Thank You So Much”) !!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!

I would like to implement dynamic programming for crossover to generate new generation solutions in genetic algorithms. Can anyone suggest how to approach.

The code is well-formatted but the logical part is still not clear. Can anyone please explain the lines of code clearly in brief?

int completed_visit = (1<<n) -1; what dose this line of code means?

Leave a Reply Cancel reply

Your email address will not be published. Required fields are marked *

Please enable JavaScript to submit this form.

Related Posts

• Deletion of any Non-ascii characters present in C++
• Program to solve the knapsack problem in C++
• CODECHEF April Cook-off ( Div. 2 ) – Making a Meal in C++

Search code, repositories, users, issues, pull requests...

Provide feedback.

We read every piece of feedback, and take your input very seriously.

Saved searches

Use saved searches to filter your results more quickly.

To see all available qualifiers, see our documentation .

• Notifications

Solve travelling salesman problem using dynamic programming.

kristiansandratama/travelling-salesman-problem-dynamic-programming

• Python 100.0%

• Coding Problems

Travelling Salesman Problem (TSP)

Problem statement, example 1: travelling salesman problem, example 2: travelling salesman problem, 1. simple approach, c++ code implementation, java code implementation, python code implementation, 2. travelling salesman problem using dynamic programming, c code implementation, 3. greedy approach, practice questions, frequently asked questions, 1. which algorithm is used for the travelling salesman problem, 2. what is the complexity of the travelling salesman problem, 3. how is this problem modelled as a graph problem, 4: what is the difficulty level of the travelling salesman problem.

Travelling Salesman Problem (TSP) – Given a set of cities and the distance between every pair of cities as an adjacency matrix, the problem is to find the shortest possible route that visits every city exactly once and returns to the starting point. The ultimate goal is to minimize the total distance travelled, forming a closed tour or circuit.

The TSP is referred to as an NP-hard problem, meaning there is no known algorithm to solve it in polynomial time for large instances. As the number of cities increases, the number of potential solutions grows exponentially, making an exhaustive search unfeasible. This complexity is one of the reasons why the TSP remains a popular topic of research. Learn More .

Input –

Confused about your next job?

Output –

Here, the TSP Tour is 0-2-1-3-0 and the cost of the tour is 48.

Minimum weight Hamiltonian Cycle : EACBDE= 32

Wondering how the Hamiltonian Cycle Problem and the Traveling Salesman Problem differ? The Hamiltonian Cycle problem is to find out if there exists a tour that visits each city exactly once. Here, we know that the Hamiltonian Tour exists (due to the graph being complete), and there are indeed many such tours. The problem is to find a minimum weight Hamiltonian Cycle.

There are various approaches to finding the solution to the travelling salesman problem- simple (naïve) approach, dynamic programming approach, and greedy approach. Let’s explore each approach in detail:

• Consider city 1 as the starting and ending point. Since the route is cyclic, we can consider any point as a starting point.
• Now, we will generate all possible permutations of cities which are (n-1)!.
• Find the cost of each permutation and keep track of the minimum cost permutation.
• Return the permutation with minimum cost.
• Time complexity: O(N!), Where N is the number of cities.
• Space complexity: O(1).

In the travelling salesman problem algorithm, we take a subset N of the required cities that need to be visited, the distance among the cities dist, and starting cities s as inputs. Each city is identified by a unique city id which we say like 1,2,3,4,5………n

Here we use a dynamic approach to calculate the cost function Cost(). Using recursive calls, we calculate the cost function for each subset of the original problem.

To calculate the cost(i) using Dynamic Programming , we need to have some recursive relation in terms of sub-problems.

We start with all subsets of size 2 and calculate C(S, i) for all subsets where S is the subset, then we calculate C(S, i) for all subsets S of size 3 and so on.

There are at most O(n2^n) subproblems, and each one takes linear time to solve. The total running time is, therefore, O(n^22^n). The time complexity is much less than O(n!) but still exponential. The space required is also exponential.

• Time Complexity: O(N^2*2^N).
• First of them is a list that can hold the indices of the cities in terms of the input matrix of distances between cities
• And the Second one is the array which is our result
• Perform traversal on the given adjacency matrix tsp[][] for all the cities and if the cost of reaching any city from the current city is less than the current cost update the cost.
• Generate the minimum path cycle using the above step and return their minimum cost.
• Time complexity: O(N^2*logN), Where N is the number of cities.
• Space complexity: O(N).
• City Tour Problem
• Shortest Common Substring

Ans . Travelling Salesman Problem uses Dynamic programming with a masking algorithm.

Ans.: The complexity of TSP using Greedy will be O(N^2 LogN) and using DP will be O(N^2 2^N).

Ans .: The TSP can be modelled as a graph problem by considering a complete graph G = (V, E). A tour is then a circuit in G that meets every node. In this context, tours are sometimes called Hamiltonian circuits.

Ans.: It is an NP-hard problem.

• Travelling Salesman Problem

Previous Post

Longest common subsequence, minimum spanning tree – kruskal algorithm.

Travelling Salesman Problem in C and C++

Here you will learn about Travelling Salesman Problem (TSP) with example and also get a program that implements Travelling Salesman Problem in C and C++.

Let say there are some villages (1, 2, 3, 4, 5). To work with worst case let assume each villages connected with every other villages. And there is a Salesman living in village 1 and he has to sell his things in all villages by travelling and he has to come back to own village 1.

He has to travel each village exactly once, because it is waste of time and energy that revisiting same village. This is same as visiting each node exactly once, which is Hamiltonian Circuit . But our problem is bigger than Hamiltonian cycle because this is not only just finding Hamiltonian path, but also we have to find shortest path.

Finally the problem is we have to visit each vertex exactly once with minimum edge cost in a graph.

Brute Force Approach takes O (n n ) time, because we have to check (n-1)! paths (i.e all permutations) and have to find minimum among them.

The correct approach for this problem is solving using Dynamic Programming.

Dynamic Programming can be applied only if main problem can be divided into sub-problems. Let’s check that.

Travelling Salesman Problem (TSP) Using Dynamic Programming

Example problem.

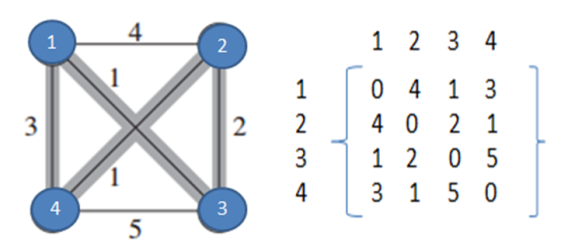
Above we can see a complete directed graph and cost matrix which includes distance between each village. We can observe that cost matrix is symmetric that means distance between village 2 to 3 is same as distance between village 3 to 2.

Here problem is travelling salesman wants to find out his tour with minimum cost.

Say it is T (1,{2,3,4}), means, initially he is at village 1 and then he can go to any of {2,3,4}. From there to reach non-visited vertices (villages) becomes a new problem. Here we can observe that main problem spitted into sub-problem, this is property of dynamic programming.

Note: While calculating below right side values calculated in bottom-up manner. Red color values taken from below calculations.

T ( 1, {2,3,4} ) = minimum of

= { (1,2) + T (2,  {3,4} )     4+ 6 =10

= { (1,3)  + T (3, {2,4} )     1+ 3 =4

= { (1,4) + T (4, {2,3} )     3+ 3 =6

Here minimum of above 3 paths is answer but we know only values of (1,2) , (1,3) , (1,4) remaining thing which is T ( 2, {3,4} ) …are new problems now. First we have to solve those and substitute here.

T (2, {3,4} )   = minimum of

=  { (2,3) + T (3, {4} )     2+ 5 =7

= { (2,4) + T {4, {3} )     1+ 5 =6

T (3, {2,4} )   = minimum of

=  { (3,2) + T (2, {4} )     2+ 1 =3

= { (3,4) + T {4, {2} )     5+ 1 =6

T (4, {2,3} )   = minimum of

=  { (4,2) + T (2, {3} )     1+ 2 =3

= { (4,3) + T {3, {2} )     5+ 2 =7

T ( 3, {4} ) =  (3,4) + T (4, {} )     5+0=5

T ( 4, {3} ) =  (4,3) + T (3, {} )     5+0=5

T ( 2, {4} ) =  (2,4) + T (4, {} )     1+0=1

T ( 4, {2} ) =  (4,2) + T (2, {} )     1+0 = 1

T ( 2, {3} ) =  (2,3) + T (3, {} )     2+0 = 2

T ( 3, {2} ) =  (3,2) + T (2, {} )     2+0=2

Here T ( 4, {} ) is reaching base condition in recursion, which returns 0 (zero ) distance.

This is where we can find final answer,

= { (1,2) + T (2,  {3,4} )     4+ 6 =10 in this path we have to add +1 because this path ends with 3. From there we have to reach 1 so 3->1 distance 1 will be added total distance is 10+1=11

= { (1,3)  + T (3, {2,4} )     1+ 3 =4 in this path we have to add +3 because this path ends with 3. From there we have to reach 1 so 4->1 distance 3 will be added total distance is 4+3=7

= { (1,4) + T (4, {2,3} )     3+ 3 =6 in this path we have to add +1 because this path ends with 3. From there we have to reach 1 so 3->1 distance 1 will be added total distance is 6+1=7

Minimum distance is 7 which includes path 1->3->2->4->1.

After solving example problem we can easily write recursive equation.

Recursive Equation

T (i , s) = min ( ( i , j) + T ( j , S – { j }) ) ;  S!= Ø   ; j € S ;

S is set that contains non visited vertices

=  ( i, 1 ) ;  S=Ø, This is base condition for this recursive equation.

T (i, S) means We are travelling from a vertex “i” and have to visit set of non-visited vertices  “S” and have to go back to vertex 1 (let we started from vertex 1).

( i, j ) means cost of path from node i  to node j

If we observe the first recursive equation from a node we are finding cost to all other nodes (i,j) and from that node to remaining using recursion ( T (j , {S-j}))

But it is not guarantee that every vertex is connected to other vertex then we take that cost as infinity. After that we are taking minimum among all so the path which is not connected get infinity in calculation and won’t be consider.

If S is empty that means we visited all nodes, we take distance from that last visited node to node 1 (first node). Because after visiting all he has to go back to initial node.

Time Complexity

Since we are solving this using Dynamic Programming, we know that Dynamic Programming approach contains sub-problems.

Here after reaching i th node finding remaining minimum distance to that i th node is a sub-problem.

If we solve recursive equation we will get total (n-1) 2 (n-2)   sub-problems, which is O (n2 n ) .

Each sub-problem will take  O (n) time (finding path to remaining (n-1) nodes).

Therefore total time complexity is O (n2 n ) * O (n) = O (n 2 2 n )

Space complexity is also number of sub-problems which is O (n2 n )

Program for Travelling Salesman Problem in C

Enter the number of villages: 4

Enter the Cost Matrix

Enter Elements of Row: 1 0 4 1 3

Enter Elements of Row: 2 4 0 2 1

Enter Elements of Row: 3 1 2 0 5

Enter Elements of Row: 4 3 1 5 0 The cost list is: 0 4 1 3 4 0 2 1 1 2 0 5 3 1 5 0

The Path is: 1—>3—>2—>4—>1

Minimum cost is 7

Program for Travelling Salesman Problem in C++

Comment below if you found any information incorrect or have doubts regarding Travelling Salesman Problem algorithm.

Related Posts

Quick sort in c [program & algorithm], evaluation of postfix expression in c [algorithm and program], infix to postfix conversion in c [program and algorithm], dfs in c [program+algorithm], 49 thoughts on “travelling salesman problem in c and c++”.

Nicely explained. I was just trying to understand the code to implement this. What I was not able to understand is why we are adding the return to the same node as well for the minimum comparison. Will the below changed least code not work for all situation ?

int least(int c) { int i,nc=999; int min=999,kmin;

for(i=0;i < n;i++) { if((ary[c][i]!=0)&&(completed[i]==0)) if(ary[c][i] < min) /* REPLACED */ { min=ary[c][i]; /* REPLACED */ kmin=ary[c][i]; nc=i; } } if(min!=999) cost+=kmin; return nc; }

Sir can u please explain this function

hellow mam your code is not work properly (for selecting minimum path) because i insert a cost matrix input 0 7 3 4 0 2 9 1 0 this cost matrix currect answer is==>8 and also travel a vertex in 1–>3–>2–>1 But your code is only work with a order wise selection example it will travel only with 1–>2–>3–>1. etc…………….

Are you for real? Are you that dumb?

this is an undirected graph. 1->3->2->1 is exactly the same as 1->2->3->1.

go ahead, bob your head.

Hi Good explanation (: But… is it posible to do TSP problem in C without the recursion?

Your Dynamic TSP-Code might not work correctly for more than 4 cities. Looping over all subsets of a set is a challenge for Programmers.

Quote: Your Dynamic TSP-Code might not work correctly for more than 4 cities.

It doesn’t. I tried it for 6 and it fails to find the minimum path. Example cost matrix and found path:

The cost list is: 0 5 9 12 4 8 5 0 4 7 9 7 9 4 0 5 5 11 12 7 5 0 10 14 4 9 5 10 0 12 8 7 11 14 12 0

The Path is: 1—>5—>3—>2—>6—>4—>1 (cost 46)

But the path 1->2->3->4->5->6->1 has cost 44

This code is NOT correct. Also every other site has this same exact code. Some one please share the link to a correct working code for solving TSP using Dynamic Programming approach.

Actually this is TSP code,he is making us fool.Watch Tushar Roy video for real Dp implementation.

Thank you so much for this resource. Why do these sites go on copying I don’t understand.

Yes, you are correct…..

min=ary[i][0]+ary[c][i]; has to be min=ary[i][c]+ary[c][i]; this migth solve the issue with the above code

Thannnnnnnnnnnnnks

it didnt solve the code…

Is the code written using dynamic approach?

NO,it is greedy ,this not for TSP,it for MST

Isn’t this the branch and bound method?

what if I do not want him to go back to starting node ?

I’m pretty sure that this is just another implementation of the nearest neighbor algorithm….

it will be better if you could add more explanation about these above functions such as takeInput(), least(), minCost(). I am really hard to understand your code.

Nice..can i ask you something..how we want to assign a value of the array with specific value..is that possible for an array consists 2 value..its more like we put the coordinate in one array..

Thank you friend. I was trying to implement one here and yours came to save my work. Now I’m sorry in the heuristic way. hugs Att. Anderson Itacoatiara – Amazonas – Brazil

I ran this for 10 cities. It ran fine, but total cost for my matrix of random costs was 138, which is higher than the 125 cost with another program which gave a result of 1 10 9 8 7 6 5 4 3 2 1, which is clearly not a valid calculation. Sigh…

Well, the thought was there, just not carried to correct completion.

The explanation is solid but the code is wrong. In each recursion step only the closest next hop in regards to the starting city is calculated, but you really have to check ALL sub-problems. The recursion doesn’t do anything special here and could as well have been a for-loop. Just check the following matrix where the start point 1 has a large cost to the furthest city 4:

“The cost list is: 0 1 1 99 1 0 1 1 1 1 0 1 99 1 1 0

The Path is: 1—>2—>3—>4—>1

Minimum cost is 102”

When obviously this could have been just 4 cost with 1->2->4->3->1

Dude checkout your code it does not work for all case; int adj_matx[4][4] = {{0,10,15,20},{10,0,35,25},{15,35,0,30},{20,25,30,0}}; //ans: 80 int adj_matx[4][4] = {{0,4,1,3},{4,0,2,1},{1,2,0,5},{3,1,5,0}}; //ans: 7 int adj_matx[5][5] = {{0,100,300,100,75},{100,0,50,75,125},{300,50,0,100,125},{100,75,100,0,50},{75,125,125,50,0}}; //ans: 375 int adj_matx[4][4] = {{0,2,1,3},{2,0,4,100},{1,4,0,2},{3,100,2,0}}; //ans: 11 int adj_matx[4][4] = {{0,2,1,4},{2,0,4,3},{1,4,0,2},{4,3,2,0}}; //ans: 8 int adj_matx[4][4] = {{0,5,6,3},{5,0,3,6},{6,3,0,7},{3,6,7,0}}; //ans: 18 int adj_matx[5][5] = {{0,6,9,100,10},{6,0,11,100,100},{9,11,0,100,14},{100,100,100,0,8},{10,100,14,8,0}}; //ans:57

for the last case if starting node is 1 then path is 1-5-4-3-2-1 and cost is 135

I second that. Saurabh is correct.

———————-T ( 1,{ 2 3 4 5 })——————— Pairwise cost { 6 9 100 10 } Subproblem cost { 129 128 39 125 } Sum cost { 135 137 139 135 } Sub Paths Printing Matrix 5 4 3 2 2 4 5 3 2 3 5 4 2 3 4 5 Choosing subpath 0 Path Vector { 5 4 3 2 1 }

Time complexity of given code is n!

Your Program is good but it is not working for more than 4 cities.

I have never commented on any website. But i was compelled to do so this time. I have been reading your blog for a long time and i find explanations and code far easier than other websites. It’s amazing and very helpful.

U r finding this code for TSP simple bczz it is completely wrong.This is code of MST,using greedy.

0 9 8 8 12 0 13 6 10 9 0 5 20 15 10 0

for this matrix the solution should be 35 (1-2-4-3-1)but by using this code it give 40(1-3-4-2-1). and also this approach is not dynamic it is greedy.

Can any one write code to display all possible paths and their respective sum of that path

Why we declare a value 999 ?

Replace: min=ary[i][0]+ary[c][i]; to: min=ary[i][c]+ary[c][i];

now works :))

No it will not

hello can you pls give program travelling sales man using branch and bound

The Algorithm has this result : The cost list is: 0 10 15 20 10 0 35 25 15 35 0 30 20 25 30 0

The Path is: 1—>;2—>;3—>;4—>;1

Minimum cost is 95 But the correct minimum cost is 80 and the correct path is 1–>2–>4–>3–>1

not showing optimal path.

Function least should have a prototype error occurs here so pls check it out

The code is totally wrong and all the explanation is being plagarized.

It is not working correctly for testcase 4 0 5 15 15 5 0 3 7 15 3 0 10 15 7 10 0 Output is : 1—>2—>4—>3—>1 cost 37 Output should be: 1—>2—>3—>4—>1 cost 33

Crazy bro.. Code is not working bro….

can any one know program of TSP then pls share

Hi, I’m sorry but your code is wrong. Please make the required changes or at least remove the code.

I mean how can you be so wrong?You wrote the explanation so nicely(probably you copied that too) and then this shit code which is present all over the internet just for wasting our time.Dont create such rubbish posts if you dont know how to implement the algorithm.

The code is really helpful but I request you to add comments. A commented code helps a way better.

Leave a Comment Cancel Reply

Your email address will not be published. Required fields are marked *

• Interview Problems on DP
• Practice DP
• Tutorial on Dynamic Programming
• Optimal Substructure
• Overlapping Subproblem
• Memoization
• Tabulation vs Memoization
• 0/1 Knapsack
• Unbounded Knapsack
• Coin Change
• Egg Dropping Puzzle
• Matrix Chain Multiplication
• Palindrome Partitioning
• DP on Arrays
• DP with Bitmasking
• DP on Trees
• DP on Graph
• Bitwise Algorithms
• Introduction to Bitwise Algorithms - Data Structures and Algorithms Tutorial
• Bitwise Operators in C
• Bitwise Operators in Java
• Python Bitwise Operators
• JavaScript Bitwise Operators
• All about Bit Manipulation
• Little and Big Endian Mystery
• Bits manipulation (Important tactics)

Easy Problems on Bit Manipulations and Bitwise Algorithms

• Binary representation of a given number
• Count set bits in an integer
• Add two bit strings
• Turn off the rightmost set bit
• Rotate bits of a number
• Compute modulus division by a power-of-2-number
• Find the Number Occurring Odd Number of Times
• Program to find whether a given number is power of 2
• Find position of the only set bit
• Check for Integer Overflow
• Find XOR of two number without using XOR operator
• Check if two numbers are equal without using arithmetic and comparison operators
• Detect if two integers have opposite signs
• How to swap two numbers without using a temporary variable?
• Russian Peasant (Multiply two numbers using bitwise operators)

Medium Problems on Bit Manipulations and Bitwise Algorithms

• Swap bits in a given number
• Smallest of three integers without comparison operators
• Compute the minimum or maximum of two integers without branching
• Smallest power of 2 greater than or equal to n
• Program to find parity
• Check if binary representation of a number is palindrome
• Generate n-bit Gray Codes
• Check if a given number is sparse or not
• Euclid's Algorithm when % and / operations are costly
• Calculate square of a number without using *, / and pow()
• Copy set bits in a range
• Check if a number is Bleak
• Gray to Binary and Binary to Gray conversion

Hard Problems on Bit Manipulations and Bitwise Algorithms

• Next higher number with same number of set bits
• Find the maximum subarray XOR in a given array
• Find longest sequence of 1's in binary representation with one flip
• Closest (or Next) smaller and greater numbers with same number of set bits

Bitmasking and Dynamic Programming | Travelling Salesman Problem

• Compute the parity of a number using XOR and table look-up
• XOR Encryption by Shifting Plaintext
• Count pairs in an array which have at least one digit common
• Python program to convert floating to binary
• Booth’s Multiplication Algorithm
• Number of pairs with Pandigital Concatenation
• Find the n-th number whose binary representation is a palindrome
• Find the two non-repeating elements in an array of repeating elements/ Unique Numbers 2
• Builtin functions of GCC compiler

In this post, we will be using our knowledge of dynamic programming and Bitmasking technique to solve one of the famous NP-hard problem “Traveling Salesman Problem”. Before solving the problem, we assume that the reader has the knowledge of   

• DP and formation of DP transition relation
• Bitmasking in DP
• Traveling Salesman problem

To understand this concept lets consider the below problem :  Problem Description :   

The above problem is the well-known Travelling Salesman Problem. The first part is to calculate the minimum distance between the two cells. We can do it by simply using a BFS as all the distances are unit distance. To optimize our solution we will be pre-calculating the distances taking the initial location and the location of the houses as the source point for our BFS. Each BFS traversal takes O(size of grid) time. Therefore, it is O(X * size_of_grid) for overall pre-calculation, where X = number of houses + 1 (initial position) Now let’s think of a DP state   So we will be needing to track the visited houses and the last visited house to uniquely identify a state in this problem. Therefore, we will be taking dp[index][mask] as our DP state.   

Here,  index : tells us the location of current house mask : tells us the houses that are visited ( if ith bit is set in mask then this means that the ith dirty tile is cleaned)   

Whereas dp[index][mask] will tell us the minimum distance to visit X(number of set bits in mask) houses corresponding to their order of their occurrence in the mask where the last visited house is house at location index. State transition relation So our initial state will be dp[0][0] this tells that we are currently at initial tile that is our initial location and mask is 0 that states that no house is visited till now. And our final destination state will be dp[any index][LIMIT_MASK] , here LIMIT_MASK = (1<<N) – 1   and N = number of houses. Therefore our DP state transition can be stated as   

The above relation can be visualized as the minimum distance to visit all the houses by standing at curr_idx house and by already visiting cur_mask houses is equal to min of distance between the curr_idx house and idx house + minimum distance to visit all the houses by standing at idx house and by already  visiting ( cur_mask | (1 <<idx) ) houses. So, here we iterate over all possible idx values such that cur_mask has i th bit as 0 that tells us that i th house is not visited. Whenever we have our mask = LIMIT_MASK, this means that we have visited all the houses in the town. So, we will add the distance from the last visited town (i.e the town at cur_idx position) to the initial position (0, 0). The C++ program for the above implementation is given below:  

The given grid :  . . . . . * .  . . . # . . .  . * . # . * .  . . . . . . .  Minimum distance for the given grid : 16 The given grid :  . . . # . . .  . . . # . * .  . . . # . . .  . * . # . * .  . . . # . . .  Minimum distance for the given grid : not possible

Output:   

Note : We have used the initial state to be dp[0][1] because we have pushed the start location at the first position in the container of houses. Hence, our Bit Mask will be 1 as the 0 th bit is set i.e we have visited the starting location for our trip.

Time Complexity : O(n 2 * 2 n ) Consider the number of houses to be n . So, there are n * (2 n ) states and at every state, we are looping over n houses to transit over to next state and because of memoization we are doing this looping transition only once for each state. Auxiliary space: O(n * 2 n ), due to the memoization of the dp states.

Recommended :   

• http://www.spoj.com/problems/CLEANRBT/
• https://www.youtube.com/watch?v=-JjA4BLQyqE

Please Login to comment...

• Dynamic Programming
• How to Delete Whatsapp Business Account?
• Discord vs Zoom: Select The Efficienct One for Virtual Meetings?
• Otter AI vs Dragon Speech Recognition: Which is the best AI Transcription Tool?
• Google Messages To Let You Send Multiple Photos
• 30 OOPs Interview Questions and Answers (2024)

Improve your Coding Skills with Practice

What kind of Experience do you want to share?

Travelling Salesman Problem: Python, C++ Algorithm

What is the Travelling Salesman Problem (TSP)?

Travelling Salesman Problem (TSP) is a classic combinatorics problem of theoretical computer science. The problem asks to find the shortest path in a graph with the condition of visiting all the nodes only one time and returning to the origin city.

The problem statement gives a list of cities along with the distances between each city.

Objective: To start from the origin city, visit other cities only once, and return to the original city again. Our target is to find the shortest possible path to complete the round-trip route.

Example of TSP

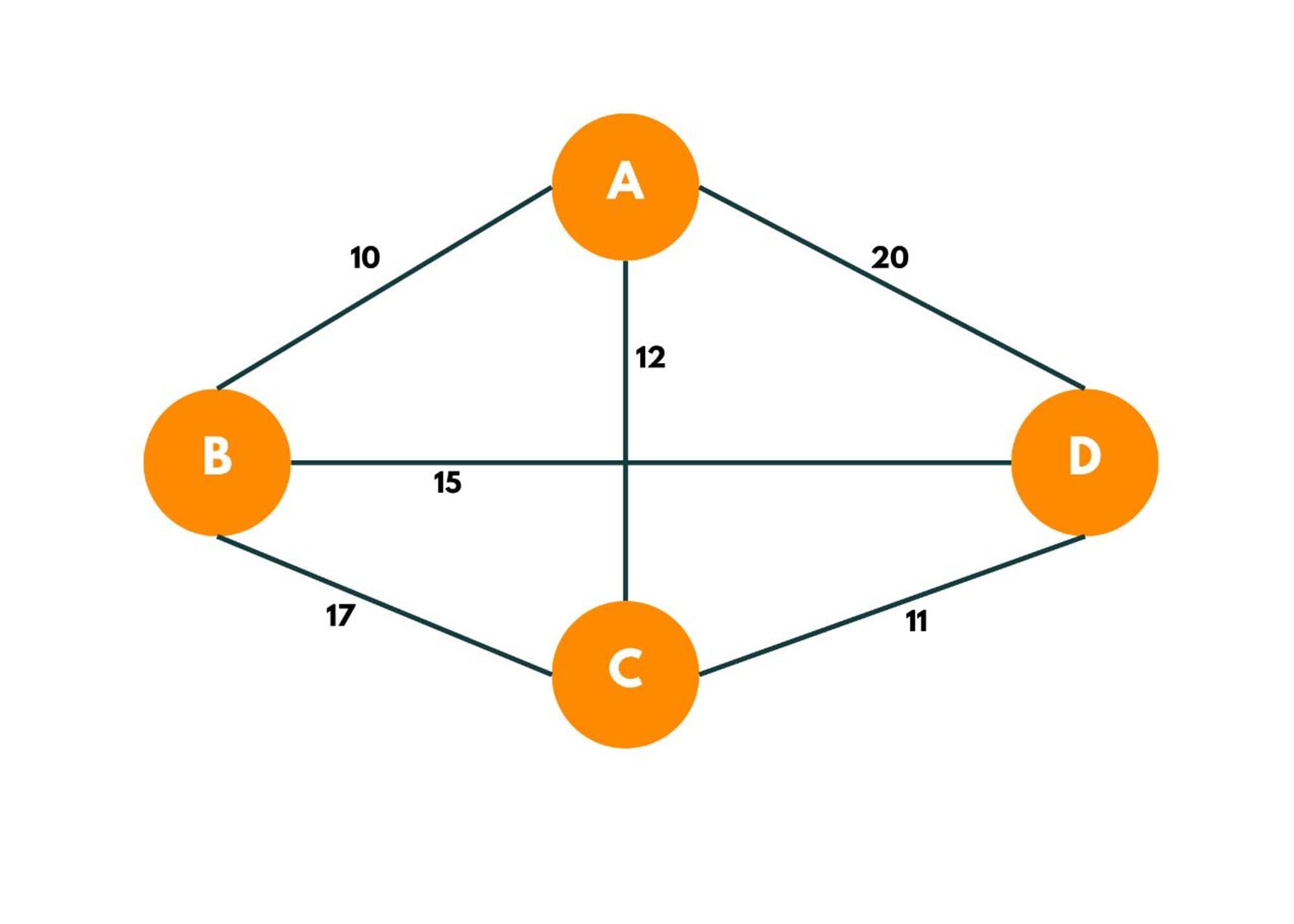
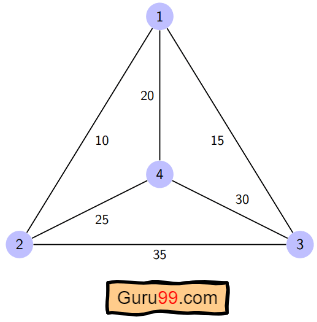
Here a graph is given where 1, 2, 3, and 4 represent the cities, and the weight associated with every edge represents the distance between those cities.

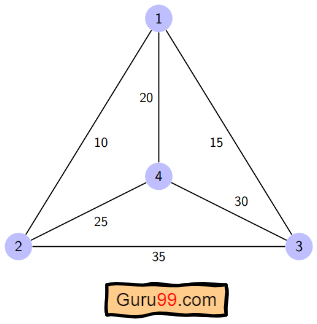
The goal is to find the shortest possible path for the tour that starts from the origin city, traverses the graph while only visiting the other cities or nodes once, and returns to the origin city.

For the above graph, the optimal route is to follow the minimum cost path: 1-2-4-3-1. And this shortest route would cost 10+25+30+15 =80

Different Solutions to Travelling Salesman Problem

Travelling Salesman Problem (TSP) is classified as a NP-hard problem due to having no polynomial time algorithm. The complexity increases exponentially by increasing the number of cities.

There are multiple ways to solve the traveling salesman problem (tsp). Some popular solutions are:

The brute force approach is the naive method for solving traveling salesman problems. In this approach, we first calculate all possible paths and then compare them. The number of paths in a graph consisting of n cities is n! It is computationally very expensive to solve the traveling salesman problem in this brute force approach.

The branch-and-bound method: The problem is broken down into sub-problems in this approach. The solution of those individual sub-problems would provide an optimal solution.

This tutorial will demonstrate a dynamic programming approach, the recursive version of this branch-and-bound method, to solve the traveling salesman problem.

Dynamic programming is such a method for seeking optimal solutions by analyzing all possible routes. It is one of the exact solution methods that solve traveling salesman problems through relatively higher cost than the greedy methods that provide a near-optimal solution.

The computational complexity of this approach is O(N^2 * 2^N) which is discussed later in this article.

The nearest neighbor method is a heuristic-based greedy approach where we choose the nearest neighbor node. This approach is computationally less expensive than the dynamic approach. But it does not provide the guarantee of an optimal solution. This method is used for near-optimal solutions.

Algorithm for Traveling Salesman Problem

We will use the dynamic programming approach to solve the Travelling Salesman Problem (TSP).

Before starting the algorithm, let’s get acquainted with some terminologies:

• A graph G=(V, E), which is a set of vertices and edges.
• V is the set of vertices.
• E is the set of edges.
• Vertices are connected through edges.
• Dist(i,j) denotes the non-negative distance between two vertices, i and j.

Let’s assume S is the subset of cities and belongs to {1, 2, 3, …, n} where 1, 2, 3…n are the cities and i, j are two cities in that subset. Now cost(i, S, j) is defined in such a way as the length of the shortest path visiting node in S, which is exactly once having the starting and ending point as i and j respectively.

For example, cost (1, {2, 3, 4}, 1) denotes the length of the shortest path where:

• Starting city is 1
• Cities 2, 3, and 4 are visited only once
• The ending point is 1

The dynamic programming algorithm would be:

• Set cost(i, , i) = 0, which means we start and end at i, and the cost is 0.
• When |S| > 1, we define cost(i, S, 1) = ∝ where i !=1 . Because initially, we do not know the exact cost to reach city i to city 1 through other cities.
• Now, we need to start at 1 and complete the tour. We need to select the next city in such a way-

cost(i, S, j)=min cost (i, S−{i}, j)+dist(i,j) where i∈S and i≠j

For the given figure, the adjacency matrix would be the following:

Let’s see how our algorithm works:

Step 1) We are considering our journey starting at city 1, visit other cities once and return to city 1.

Step 2) S is the subset of cities. According to our algorithm, for all |S| > 1, we will set the distance cost(i, S, 1) = ∝. Here cost(i, S, j) means we are starting at city i, visiting the cities of S once, and now we are at city j. We set this path cost as infinity because we do not know the distance yet. So the values will be the following:

Cost (2, {3, 4}, 1) = ∝ ; the notation denotes we are starting at city 2, going through cities 3, 4, and reaching 1. And the path cost is infinity. Similarly-

cost(3, {2, 4}, 1) = ∝

cost(4, {2, 3}, 1) = ∝

Step 3) Now, for all subsets of S, we need to find the following:

cost(i, S, j)=min cost (i, S−{i}, j)+dist(i,j), where j∈S and i≠j

That means the minimum cost path for starting at i, going through the subset of cities once, and returning to city j. Considering that the journey starts at city 1, the optimal path cost would be= cost(1, {other cities}, 1).

Let’s find out how we could achieve that:

Now S = {1, 2, 3, 4}. There are four elements. Hence the number of subsets will be 2^4 or 16. Those subsets are-

1) |S| = Null:

2) |S| = 1:

{{1}, {2}, {3}, {4}}

3) |S| = 2:

{{1, 2}, {1, 3}, {1, 4}, {2, 3}, {2, 4}, {3, 4}}

4) |S| = 3:

{{1, 2, 3}, {1, 2, 4}, {2, 3, 4}, {1, 3, 4}}

5) |S| = 4:

{{1, 2, 3, 4}}

As we are starting at 1, we could discard the subsets containing city 1.

The algorithm calculation:

1) |S| = Φ:

cost (2, Φ, 1) = dist(2, 1) = 10

cost (3, Φ, 1) = dist(3, 1) = 15

cost (4, Φ, 1) = dist(4, 1) = 20

cost (2, {3}, 1) = dist(2, 3) + cost (3, Φ, 1) = 35+15 = 50

cost (2, {4}, 1) = dist(2, 4) + cost (4, Φ, 1) = 25+20 = 45

cost (3, {2}, 1) = dist(3, 2) + cost (2, Φ, 1) = 35+10 = 45

cost (3, {4}, 1) = dist(3, 4) + cost (4, Φ, 1) = 30+20 = 50

cost (4, {2}, 1) = dist(4, 2) + cost (2, Φ, 1) = 25+10 = 35

cost (4, {3}, 1) = dist(4, 3) + cost (3, Φ, 1) = 30+15 = 45

cost (2, {3, 4}, 1) = min [ dist[2,3]+Cost(3,{4},1) = 35+50 = 85,

dist[2,4]+Cost(4,{3},1) = 25+45 = 70 ] = 70

cost (3, {2, 4}, 1) = min [ dist[3,2]+Cost(2,{4},1) = 35+45 = 80,

dist[3,4]+Cost(4,{2},1) = 30+35 = 65 ] = 65

cost (4, {2, 3}, 1) = min [ dist[4,2]+Cost(2,{3},1) = 25+50 = 75

dist[4,3]+Cost(3,{2},1) = 30+45 = 75 ] = 75

cost (1, {2, 3, 4}, 1) = min [ dist[1,2]+Cost(2,{3,4},1) = 10+70 = 80

dist[1,3]+Cost(3,{2,4},1) = 15+65 = 80

dist[1,4]+Cost(4,{2,3},1) = 20+75 = 95 ] = 80

So the optimal solution would be 1-2-4-3-1

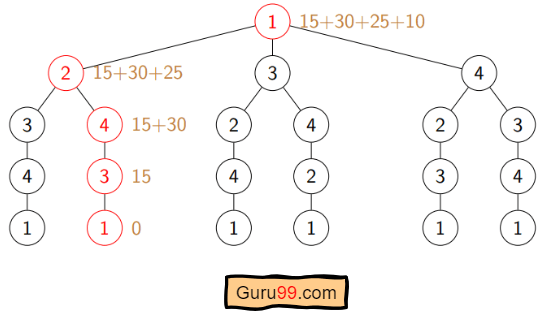
Pseudo-code

Implementation in c/c++.

Here’s the implementation in C++ :

Implementation in Python

Academic solutions to tsp.

Computer scientists have spent years searching for an improved polynomial time algorithm for the Travelling Salesman Problem. Until now, the problem is still NP-hard.

Though some of the following solutions were published in recent years that have reduced the complexity to a certain degree:

• The classical symmetric TSP is solved by the Zero Suffix Method.
• The Biogeography‐based Optimization Algorithm is based on the migration strategy to solve the optimization problems that can be planned as TSP.
• Multi-Objective Evolutionary Algorithm is designed for solving multiple TSP based on NSGA-II.
• The Multi-Agent System solves the TSP of N cities with fixed resources.

Application of Traveling Salesman Problem

Travelling Salesman Problem (TSP) is applied in the real world in both its purest and modified forms. Some of those are:

• Planning, logistics, and manufacturing microchips : Chip insertion problems naturally arise in the microchip industry. Those problems can be planned as traveling salesman problems.
• DNA sequencing : Slight modification of the traveling salesman problem can be used in DNA sequencing. Here, the cities represent the DNA fragments, and the distance represents the similarity measure between two DNA fragments.
• Astronomy : The Travelling Salesman Problem is applied by astronomers to minimize the time spent observing various sources.
• Optimal control problem : Travelling Salesman Problem formulation can be applied in optimal control problems. There might be several other constraints added.

Complexity Analysis of TSP

So the total time complexity for an optimal solution would be the Number of nodes * Number of subproblems * time to solve each sub-problem. The time complexity can be defined as O(N 2 * 2^N).

• Space Complexity: The dynamic programming approach uses memory to store C(S, i), where S is a subset of the vertices set. There is a total of 2 N subsets for each node. So, the space complexity is O(2^N).

Next, you’ll learn about Sieve of Eratosthenes Algorithm

• Linear Search: Python, C++ Example
• DAA Tutorial PDF: Design and Analysis of Algorithms
• Heap Sort Algorithm (With Code in Python and C++)
• Kadence’s Algorithm: Largest Sum Contiguous Subarray
• Radix Sort Algorithm in Data Structure
• Doubly Linked List: C++, Python (Code Example)
• Singly Linked List in Data Structures
• Adjacency List and Matrix Representation of Graph

• Interview Q

DAA Tutorial

Asymptotic analysis, analysis of sorting, divide and conquer, lower bound theory, sorting in linear time, binary search trees, red black tree, dynamic programming, greedy algorithm, backtracking, shortest path, all-pairs shortest paths, maximum flow, sorting networks, complexity theory, approximation algo, string matching.

Interview Questions

• Send your Feedback to [email protected]

Help Others, Please Share

Learn Latest Tutorials

Transact-SQL

Reinforcement Learning

R Programming

React Native

Python Design Patterns

Python Pillow

Python Turtle

Preparation

Verbal Ability

Company Questions

Trending Technologies

Artificial Intelligence

Cloud Computing

Data Science

Machine Learning

B.Tech / MCA

Data Structures

Operating System

Computer Network

Compiler Design

Computer Organization

Discrete Mathematics

Ethical Hacking

Computer Graphics

Software Engineering

Web Technology

Cyber Security

C Programming

Control System

Data Mining

Data Warehouse

Traveling Salesman Problem for a Bidirectional Graph Using Dynamic Programming

Ieee account.

• Change Username/Password
• Update Address

Purchase Details

• Payment Options
• Order History
• View Purchased Documents

Profile Information

• Communications Preferences
• Profession and Education
• Technical Interests
• US & Canada: +1 800 678 4333
• Worldwide: +1 732 981 0060
• Contact & Support
• About IEEE Xplore
• Accessibility
• Terms of Use
• Nondiscrimination Policy
• Privacy & Opting Out of Cookies

A not-for-profit organization, IEEE is the world's largest technical professional organization dedicated to advancing technology for the benefit of humanity. © Copyright 2024 IEEE - All rights reserved. Use of this web site signifies your agreement to the terms and conditions.