knight tour in graph theory

The Knight’s Tour

The  knight’s tour problem  is the mathematical problem of finding a knight’s tour, and probably making knight the most interesting piece on the chess board. The knight visits every square exactly once, if the knight ends on a square that is one knight’s move from the beginning square (so that it could tour the board again immediately, following the same path), the tour is closed; otherwise, it is open.

The knight’s tour problem is an instance of the more general Hamiltonian path problem in graph theory. The problem of finding a closed knight’s tour is similarly an instance of the Hamiltonian cycle problem. Unlike the general Hamiltonian path problem, the knight’s tour problem can be solved in linear time.

Hamiltonian Path Problem

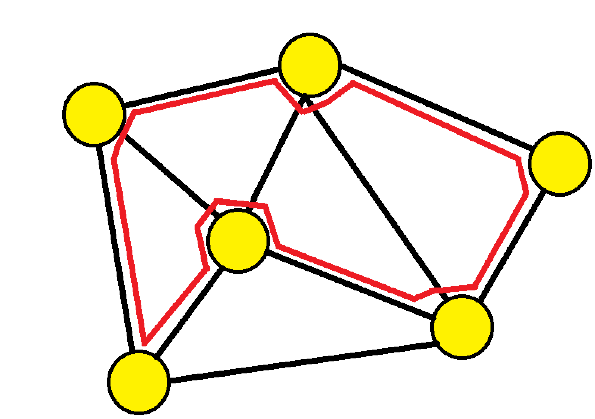
In Graph Theory, a graph is usually defined to be a collection of nodes or vertices and the set of edges which define which nodes are connected with each other. So we use a well known notation of representing a graph G = (V,E) where  V = { v 1 , v 2 , v 3 , … , v n }  and E = {(i, j)|i ∈ V and j ∈ V and i and j is connected}.

Hamiltonian Path is defined to be a single path that visits every node in the given graph, or a permutation of nodes in such a way that for every adjacent node in the permutation there is an edge defined in the graph. Notice that it does not make much sense in repeating the same paths. In order to avoid this repetition, we permute with |V| C 2 combinations of starting and ending vertices.

Simple way of solving the Hamiltonian Path problem would be to permutate all possible paths and see if edges exist on all the adjacent nodes in the permutation. If the graph is a complete graph, then naturally all generated permutations would quality as a Hamiltonian path.

For example. let us find a Hamiltonian path in graph G = (V,E) where V = {1,2,3,4} and E = {(1,2),(2,3),(3,4)}. Just by inspection, we can easily see that the Hamiltonian path exists in permutation 1234. The given algorithm will first generate the following permutations based on the combinations: 1342 1432 1243 1423 1234 1324 2143 2413 2134 2314 3124 3214

The number that has to be generated is ( |V| C 2 ) (|V| – 2)!

Schwenk proved that for any  m  ×  n  board with  m  ≤  n , a closed knight’s tour is always possible  unless  one or more of these three conditions are met:

• m  and  n  are both odd
• m  = 1, 2, or 4
• m  = 3 and  n  = 4, 6, or 8.

Cull and Conrad proved that on any rectangular board whose smaller dimension is at least 5, there is a (possibly open) knight’s tour.

Neural network solutions

The neural network is designed such that each legal knight’s move on the chessboard is represented by a neuron. Therefore, the network basically takes the shape of the  knight’s graph  over an n×n chess board. (A knight’s graph is simply the set of all knight moves on the board)

Each neuron can be either “active” or “inactive” (output of 1 or 0). If a neuron is active, it is considered part of the solution to the knight’s tour. Once the network is started, each active neuron is configured so that it reaches a “stable” state if and only if it has exactly two neighboring neurons that are also active (otherwise, the state of the neuron changes). When the entire network is stable, a solution is obtained. The complete transition rules are as follows:

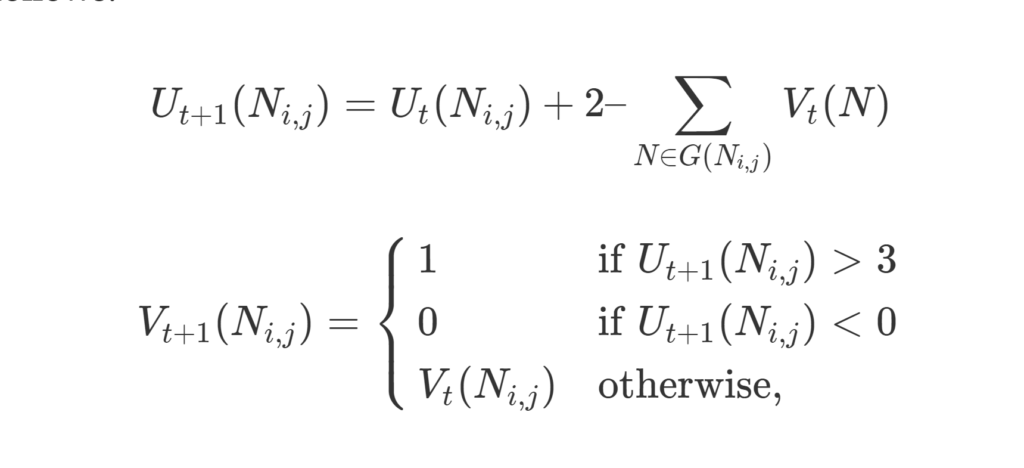
where t represents time (incrementing in discrete intervals), U(N i,j ) is the state of the neuron connecting square i to square j, V(N i,j ) is the output of the neuron from i to j, and G(N i,j ) is the set of “neighbors” of the neuron (all neurons that share a vertex with N i,j ).

Code For Knight’s Tour

You May Also Like

Gödel’s Incompleteness Theorems

Knot theory, leave a reply cancel reply.

• Contract bridge
• Connection games
• Cards classifier
• List of dice games
• Rummy games
• Chess World Cup
• FIDE Grand Prix
• World Championship
• List of strong tournaments
• List of world championships
• Checkmate patterns
• Chess openings
• Chess strategy
• Chess tactics
• Chess theory
• Pawn structure
• Problems/Compositions
• Computer chess
• Chess engines
• Chess software
• Cheating in chess
• Chess prodigy
• List of Grandmasters
• Grandmasters by country
• Top player comparison
• World rankings
• Chess titles
• Rating systems
• Correspondence chess
• List of chess variants
• Rules of chess
• Chess notation
• Outline of chess
• Timeline of chess

Knight's tour

A knight's tour is a sequence of moves of a knight on a chessboard such that the knight visits every square only once. If the knight ends on a square that is one knight's move from the beginning square (so that it could tour the board again immediately, following the same path), the tour is closed , otherwise it is open .

The knight's tour problem is the mathematical problem of finding a knight's tour. Creating a program to find a knight's tour is a common problem given to computer science students. Variations of the knight's tour problem involve chessboards of different sizes than the usual 8 x 8, as well as irregular (non-rectangular) boards.

The knight's tour problem is an instance of the more general Hamiltonian path problem in graph theory. The problem of finding a closed knight's tour is similarly an instance of the Hamiltonian cycle problem. Unlike the general Hamiltonian path problem, the knight's tour problem can be solved in linear time.

The earliest known reference to the knight's tour problem dates back to the 9th century AD. In Rudraṭa's Kavyalankara (5.15), a Sanskrit work on Poetics, the pattern of a knight's tour on a half-board has been presented as an elaborate poetic figure ("citra-alaṅkāra") called the "turagapadabandha" or 'arrangement in the steps of a horse.' The same verse in four lines of eight syllables each can be read from left to right or by following the path of the knight on tour. Since the Indic writing systems used for Sanskrit are syllabic, each syllable can be thought of as representing a square on a chess board. Rudrata's example is as follows:

से ना ली ली ली ना ना ना ली

ली ना ना ना ना ली ली ली ली

न ली ना ली ली ले ना ली ना

ली ली ली ना ना ना ना ना ली

se nā lī lī lī nā nā lī

lī nā nā nā nā lī lī lī

na lī nā lī le nā lī nā

lī lī lī nā nā nā nā lī

For example, the first line can be read from left to right or by moving from the first square to second line, third syllable (2.3) and then to 1.5 to 2.7 to 4.8 to 3.6 to 4.4 to 3.2.

One of the first mathematicians to investigate the knight's tour was Leonhard Euler. The first procedure for completing the Knight's Tour was Warnsdorf's rule, first described in 1823 by H. C. von Warnsdorf.

In the 20th century, the Oulipo group of writers used it among many others. The most notable example is the 10 x 10 Knight's Tour which sets the order of the chapters in Georges Perec's novel Life: A User's Manual . The sixth game of the 2010 World Chess Championship between Viswanathan Anand and Veselin Topalov saw Anand making 13 consecutive knight moves (albeit using both knights); online commentors jested that Anand was trying to solve the Knight's Tour problem during the game.

Schwenk proved that for any m x n board with m ≤ n , a closed knight's tour is always possible unless one or more of these three conditions are met:

• m and n are both odd
• m = 1, 2, or 4
• m = 3 and n = 4, 6, or 8.

Cull et al. and Conrad et al. proved that on any rectangular board whose smaller dimension is at least 5, there is a (possibly open) knight's tour.

Number of tours

On an 8 x 8 board, there are exactly 26,534,728,821,064 directed closed tours (i.e. two tours along the same path that travel in opposite directions are counted separately, as are rotations and reflections). The number of undirected closed tours is half this number, since every tour can be traced in reverse. There are 9,862 undirected closed tours on a 6 x 6 board.

Finding tours with computers

There are quite a number of ways to find a knight's tour on a given board with a computer. Some of these methods are algorithms while others are heuristics.

Brute force algorithms

A brute-force search for a knight's tour is impractical on all but the smallest boards; for example, on an 8x8 board there are approximately 4x10 51 possible move sequences, and it is well beyond the capacity of modern computers (or networks of computers) to perform operations on such a large set. However the size of this number gives a misleading impression of the difficulty of the problem, which can be solved "by using human insight and ingenuity ... without much difficulty."

Divide and conquer algorithms

By dividing the board into smaller pieces, constructing tours on each piece, and patching the pieces together, one can construct tours on most rectangular boards in polynomial time.

Neural network solutions

The Knight's Tour problem also lends itself to being solved by a neural network implementation. The network is set up such that every legal knight's move is represented by a neuron, and each neuron is initialized randomly to be either "active" or "inactive" (output of 1 or 0), with 1 implying that the neuron is part of the final solution. Each neuron also has a state function (described below) which is initialized to 0.

When the network is allowed to run, each neuron can change its state and output based on the states and outputs of its neighbors (those exactly one knight's move away) according to the following transition rules:

Warnsdorff's rule

Warnsdorff's rule is a heuristic for finding a knight's tour. We move the knight so that we always proceed to the square from which the knight will have the fewest onward moves. When calculating the number of onward moves for each candidate square, we do not count moves that revisit any square already visited. It is, of course, possible to have two or more choices for which the number of onward moves is equal; there are various methods for breaking such ties, including one devised by Pohl and another by Squirrel and Cull.

This rule may also more generally be applied to any graph. In graph-theoretic terms, each move is made to the adjacent vertex with the least degree. Although the Hamiltonian path problem is NP-hard in general, on many graphs that occur in practice this heuristic is able to successfully locate a solution in linear time. The knight's tour is a special case.

The heuristic was first described in "Des Rösselsprungs einfachste und allgemeinste Lösung" by H. C. von Warnsdorff in 1823. A computer program that finds a Knight's Tour for any starting position using Warnsdorff's rule can be found in the book 'Century/Acorn User Book of Computer Puzzles' edited by Simon Dally (ISBN 071260541X).

• Abu-Bakr Muhammad ben Yahya as-Suli
• George Koltanowski
• Longest uncrossed knight's path
• Eight queens puzzle

Type and hit Enter to search

Andrei Arkhipov

Software Endineer

The Knight’s Tour: A Classic Chessboard Challenge

The Knight’s Tour is a fascinating problem from the domain of computer science and mathematics, specifically within the realm of graph theory. The problem presents a curious challenge: Can a knight traverse every square of a chessboard exactly once?

The Knight’s Tour Statement

On a given N x N chessboard, determine if a knight can be moved to every square without repeating any square, starting from any initial position.

Backtracking Approach

The Knight’s Tour is typically approached via backtracking. This method involves trying out all the possible moves from a given position and, if a dead-end is encountered, reverting (or “backtracking”) to the previous step to try a different path.

JavaScript Implementation (Simplified) :

Visualizations of the Knight’s Tour

The Knight’s Tour can be wonderfully visualized, highlighting the path the knight takes. Each cell the knight visits gets numbered sequentially, indicating the move order.

Complexity and Insights

The nature of the backtracking algorithm for this problem is exponential. While efficient solutions can solve the Knight’s Tour for standard 8 x 8 chessboards, as N grows, the time taken increases rapidly. The problem is NP-hard, meaning no polynomial-time solution exists for all board sizes.

Historical Significance

The Knight’s Tour has historical roots, with mathematicians like Euler having studied it. It serves as an introduction to the “ Hamiltonian Cycle ” problem in graph theory.

The Knight’s Tour is more than just a chessboard puzzle. It bridges the world of gaming and theoretical computer science, prompting thinkers to explore the vast possibilities within constrained environments. Through backtracking and other techniques, one gets a glimpse into the methodical and recursive nature of algorithmic problem-solving.

Share Article

Related posts, big o notation: algorithm complexity & efficiency.

In the realm of computer science and software engineering, Big O Notation is a mathematical...

Balanced Binary Search Trees: A Deep Dive with JavaScript

Balanced Binary Search Trees (BBST) are a unique blend of binary search trees and balanced trees,...

Understanding Arrays: The Fundamental Data Structure

Arrays are among the most fundamental and widely-used data structures in computer programming, and...

Knight's Tour Graph

Knight Graph

• Practice Backtracking
• Interview Problems on Backtracking
• MCQs on Backtracking
• Tutorial on Backtracking
• Backtracking vs Recursion
• Backtracking vs Branch & Bound
• Print Permutations
• Subset Sum Problem
• N-Queen Problem
• Knight's Tour
• Sudoku Solver
• Rat in Maze
• Hamiltonian Cycle
• Graph Coloring
• Backtracking Algorithm
• Introduction to Backtracking - Data Structure and Algorithm Tutorials
• Difference between Backtracking and Branch-N-Bound technique
• What is the difference between Backtracking and Recursion?

Standard problems on backtracking

• The Knight's tour problem
• Rat in a Maze
• N Queen Problem
• Subset Sum Problem using Backtracking
• M-Coloring Problem
• Algorithm to Solve Sudoku | Sudoku Solver
• Magnet Puzzle
• Remove Invalid Parentheses
• A backtracking approach to generate n bit Gray Codes
• Permutations of given String

Easy Problems on Backtracking

• Print all subsets of a given Set or Array
• Check if a given string is sum-string
• Count all possible Paths between two Vertices
• Find all distinct subsets of a given set using BitMasking Approach
• Find if there is a path of more than k length from a source
• Print all paths from a given source to a destination
• Print all possible strings that can be made by placing spaces

Medium prblems on Backtracking

• 8 queen problem
• Combinational Sum
• Warnsdorff's algorithm for Knight’s tour problem
• Find paths from corner cell to middle cell in maze
• Find Maximum number possible by doing at-most K swaps
• Rat in a Maze with multiple steps or jump allowed
• N Queen in O(n) space

Hard problems on Backtracking

• Power Set in Lexicographic order
• Word Break Problem using Backtracking
• Partition of a set into K subsets with equal sum
• Longest Possible Route in a Matrix with Hurdles
• Find shortest safe route in a path with landmines
• Printing all solutions in N-Queen Problem
• Print all longest common sub-sequences in lexicographical order
• Top 20 Backtracking Algorithm Interview Questions

The Knight’s tour problem

Backtracking is an algorithmic paradigm that tries different solutions until finds a solution that “works”. Problems that are typically solved using the backtracking technique have the following property in common. These problems can only be solved by trying every possible configuration and each configuration is tried only once. A Naive solution for these problems is to try all configurations and output a configuration that follows given problem constraints. Backtracking works incrementally and is an optimization over the Naive solution where all possible configurations are generated and tried. For example, consider the following Knight’s Tour problem. 

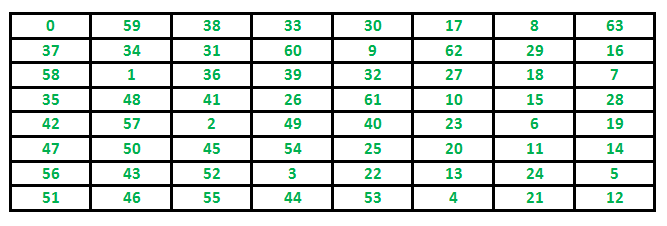
Problem Statement: Given a N*N board with the Knight placed on the first block of an empty board. Moving according to the rules of chess knight must visit each square exactly once. Print the order of each cell in which they are visited.

The path followed by Knight to cover all the cells Following is a chessboard with 8 x 8 cells. Numbers in cells indicate the move number of Knight. 

Let us first discuss the Naive algorithm for this problem and then the Backtracking algorithm.

Naive Algorithm for Knight’s tour   The Naive Algorithm is to generate all tours one by one and check if the generated tour satisfies the constraints. 

Backtracking works in an incremental way to attack problems. Typically, we start from an empty solution vector and one by one add items (Meaning of item varies from problem to problem. In the context of Knight’s tour problem, an item is a Knight’s move). When we add an item, we check if adding the current item violates the problem constraint, if it does then we remove the item and try other alternatives. If none of the alternatives works out then we go to the previous stage and remove the item added in the previous stage. If we reach the initial stage back then we say that no solution exists. If adding an item doesn’t violate constraints then we recursively add items one by one. If the solution vector becomes complete then we print the solution.

Backtracking Algorithm for Knight’s tour  

Following is the Backtracking algorithm for Knight’s tour problem. 

Following are implementations for Knight’s tour problem. It prints one of the possible solutions in 2D matrix form. Basically, the output is a 2D 8*8 matrix with numbers from 0 to 63 and these numbers show steps made by Knight.   

Time Complexity :  There are N 2 Cells and for each, we have a maximum of 8 possible moves to choose from, so the worst running time is O(8 N^2 ).

Auxiliary Space: O(N 2 )

Important Note: No order of the xMove, yMove is wrong, but they will affect the running time of the algorithm drastically. For example, think of the case where the 8th choice of the move is the correct one, and before that our code ran 7 different wrong paths. It’s always a good idea a have a heuristic than to try backtracking randomly. Like, in this case, we know the next step would probably be in the south or east direction, then checking the paths which lead their first is a better strategy.

Note that Backtracking is not the best solution for the Knight’s tour problem. See the below article for other better solutions. The purpose of this post is to explain Backtracking with an example.  Warnsdorff’s algorithm for Knight’s tour problem

References:  http://see.stanford.edu/materials/icspacs106b/H19-RecBacktrackExamples.pdf   http://www.cis.upenn.edu/~matuszek/cit594-2009/Lectures/35-backtracking.ppt   http://mathworld.wolfram.com/KnightsTour.html   http://en.wikipedia.org/wiki/Knight%27s_tour    

Please Login to comment...

Similar reads.

• chessboard-problems
• Backtracking
• Mathematical

Improve your Coding Skills with Practice

What kind of Experience do you want to share?

IB Maths Resources from Intermathematics

IB Maths Resources: 300 IB Maths Exploration ideas, video tutorials and Exploration Guides

Knight’s Tour

The Knight’s Tour is a mathematical puzzle that has endured over 1000 years.  The question is simple enough – a knight (which can move as illustrated above) wants to visit all the squares on a chess board only once.  What paths can it take?  You can vary the problem by requiring that the knight starts and finishes on the same square (a closed tour) and change the dimensions of the board.

The first recorded solution (as explained in this excellent pdf exploration of the Knight’s Tour by Ben Hill and Kevin Tostado) is shown below:

The numbers refer to the sequence of moves that the knight takes.  So, in this case the knight will start in the top right hand corner (01), before hopping to number 02.  Following the numbers around produces the pattern on the right.  This particular knight’s tour is closed as it starts and finishes at the same square and incredibly can be dated back to the chess enthusiast al-Adli ar-Rumi circa 840 AD.

Despite this puzzle being well over 1000 years old, and despite modern computational power it is still unknown as to how many distinct knight’s tours there are for an 8×8 chess board.  The number of distinct paths are as follows:

1×1 grid: 1, 2×2 grid: 0, 3×3 grid: 0, 4×4 grid: 0, 5×5 grid: 1728, 6×6 grid: 6,637,920, 7×7 grid: 165,575,218,320 8×8 grid: unknown

We can see just how rapidly this sequence grows by going from 6×6 to 7×7 – so the answer for the 8×8 grid must be huge.  Below is one of the 1728 solutions to the 5×5 knight’s tour:

You might be wondering if this has any applications beyond being a diverting puzzle, well Euler – one of the world’s true great mathematicians – used knight’s tours in his study of graph theory.  Graph theory is an entire branch of mathematics which models connections between objects.

Knight’s tours have also been used for cryptography:

This code is from the 1870s and exploits the huge number of possible knight’s tours for an 8×8 chess board.  You would require that the recipient of your code knew the tour solution (bottom left) in advance.  With this solution key you can read the words in order – first by finding where 1 is in the puzzle (row 6 column 3) – and seeing that this equates to the word “the”.  Next we see that 2 equates to “man” and so on.  Without the solution key you would be faced with an unimaginably large number of possible combinations – making cracking the code virtually impossible.

If you are interested in looking at some more of the maths behind the knight’s tour problem then the paper by Ben Hill and Kevin Tostado referenced above go into some more details.  In particular we have the following rules:

An m x n chessboard with m less than or equal to n has a knight’s tour unless one or more of these three conditions hold:

1) m and n are both odd 2) m = 1, 2 or 4 3) m = 3 and n = 4,6,8

Investigate why this is!

If you enjoyed this post you might also like:

e’s are good – He’s Leonard Euler. A discussion about the amazing number e and Euler’s use of graph theory.

Sierpinski Triangles and Spirolateral Investigation Lesson Plan. A lesson to introduce the mathematics in art and fractals.

Essential resources for IB students:

1) Exploration Guides  and Paper 3 Resources

I’ve put together four comprehensive pdf guides to help students prepare for their exploration coursework and Paper 3 investigations. The exploration guides talk through the marking criteria, common student mistakes, excellent ideas for explorations, technology advice, modeling methods and a variety of statistical techniques with detailed explanations. I’ve also made 17 full investigation questions which are also excellent starting points for explorations.  The Exploration Guides can be downloaded here  and the Paper 3 Questions can be downloaded here .

Share this:

Leave a reply cancel reply.

Powered by WordPress.com .

Discover more from IB Maths Resources from Intermathematics

Subscribe now to keep reading and get access to the full archive.

Type your email…

Continue reading

• Runestone in social media: Follow @iRunestone Our Facebook Page
• Table of Contents
• Assignments
• Peer Instruction (Instructor)
• Peer Instruction (Student)
• Change Course
• Instructor's Page
• Progress Page
• Edit Profile
• Change Password
• Scratch ActiveCode
• Scratch Activecode
• Instructors Guide
• About Runestone
• Report A Problem
• 8.1 Objectives
• 8.2 Vocabulary and Definitions
• 8.3 The Graph Abstract Data Type
• 8.4 An Adjacency Matrix
• 8.5 An Adjacency List
• 8.6 Implementation
• 8.7 The Word Ladder Problem
• 8.8 Building the Word Ladder Graph
• 8.9 Implementing Breadth First Search
• 8.10 Breadth First Search Analysis
• 8.11 The Knight’s Tour Problem
• 8.12 Building the Knight’s Tour Graph
• 8.13 Implementing Knight’s Tour
• 8.14 Knight’s Tour Analysis
• 8.15 General Depth First Search
• 8.16 Depth First Search Analysis
• 8.17 Topological Sorting
• 8.18 Strongly Connected Components
• 8.19 Shortest Path Problems
• 8.20 Dijkstra’s Algorithm
• 8.21 Analysis of Dijkstra’s Algorithm
• 8.22 Prim’s Spanning Tree Algorithm
• 8.23 Summary
• 8.24 Key Terms
• 8.25 Discussion Questions
• 8.26 Programming Exercises
• 8.11. The Knight’s Tour Problem" data-toggle="tooltip">
• 8.13. Implementing Knight’s Tour' data-toggle="tooltip" >

8.12. Building the Knight’s Tour Graph ¶

To represent the knight’s tour problem as a graph we will use the following two ideas: Each square on the chessboard can be represented as a node in the graph. Each legal move by the knight can be represented as an edge in the graph. Figure 1 illustrates the legal moves by a knight and the corresponding edges in a graph.

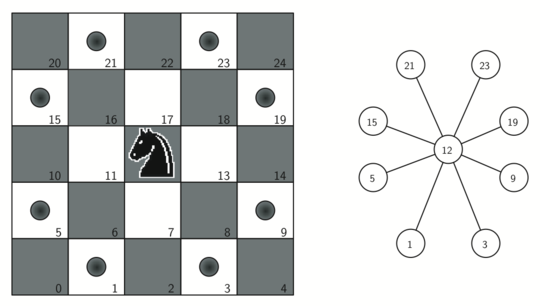
Figure 1: Legal Moves for a Knight on Square 12, and the Corresponding Graph ¶

To build the full graph for an n-by-n board we can use the Python function shown in Listing 1 . The knightGraph function makes one pass over the entire board. At each square on the board the knightGraph function calls a helper, genLegalMoves , to create a list of legal moves for that position on the board. All legal moves are then converted into edges in the graph. Another helper function posToNodeId converts a location on the board in terms of a row and a column into a linear vertex number similar to the vertex numbers shown in Figure 1 .

The genLegalMoves function ( Listing 2 ) takes the position of the knight on the board and generates each of the eight possible moves. The legalCoord helper function ( Listing 2 ) makes sure that a particular move that is generated is still on the board.

Figure 2 shows the complete graph of possible moves on an eight-by-eight board. There are exactly 336 edges in the graph. Notice that the vertices corresponding to the edges of the board have fewer connections (legal moves) than the vertices in the middle of the board. Once again we can see how sparse the graph is. If the graph was fully connected there would be 4,096 edges. Since there are only 336 edges, the adjacency matrix would be only 8.2 percent full.

Figure 2: All Legal Moves for a Knight on an \(8 \times 8\) Chessboard ¶

• Mission and Vision
• Annual Reports
• Complaints Procedures
• Delegates Information
• Executive Board
• Staff/Contact Us
• Requests for Proposals (RFP)
• Job Postings
• Guide to a Successful Chess Club
• The Ratings System
• New to National Events Guide
• Safe Play Policy
• How to Send an Email Blast
• Guide to Scholastic Chess
• Accessibility Guidelines
• Our Initiative
• Top 100 Lists
• Olympiad Campaign
• At-Risk Youth
• Correspondence Chess
• 2023-24 Scholastic Regulations
• Scholastic Council Members
• Chess Life Kids Online
• Faces of US Chess
• Our Heritage: Yearbook
• Upcoming Events
• Grants/Awards
• Spectator Policy at Scholastics
• Current Scholastic Regulations
• Event Bidding
• Official Rules
• Plan Ahead Calendar
• Grand Prix Information
• Pan American Youth Championships
• Pan Am Youth Champ
• Irwin: Seniors (50+)
• Denker: HS (9-12)
• Haring: Girls (K-12)
• Barber: MS (6-8)
• Rockefeller: ES (K-5)
• Weeramantry: Blitz
• Player/Ratings Look-Up
• Past Event Crosstables
• Events Rated List
• TD/Affiliate Support
• Club/Affiliate Search
• Rating System Algorithm
• MSA/Ratings FAQ
• Become a Member
• Become an Affiliate
• Redeem a Voucher
• Benefactor Members
• Membership Form PDF
• Info for Members/Affiliates
• Donor Bill of Rights
• Giving Tuesday
• Donate Online
• Case for Support
• At-Risk-Youth

Chess and Math: A Closer Look at the Knight's Tour

• April 2024 (41)
• March 2024 (34)
• February 2024 (25)
• January 2024 (26)
• December 2023 (29)
• November 2023 (26)
• October 2023 (38)
• September 2023 (27)
• August 2023 (37)
• July 2023 (47)
• June 2023 (33)
• May 2023 (37)
• April 2023 (45)
• March 2023 (37)
• February 2023 (28)
• January 2023 (31)
• December 2022 (23)
• November 2022 (32)
• October 2022 (31)
• September 2022 (19)
• August 2022 (39)
• July 2022 (32)
• June 2022 (35)
• May 2022 (21)
• April 2022 (31)
• March 2022 (33)
• February 2022 (21)
• January 2022 (27)
• December 2021 (36)
• November 2021 (34)
• October 2021 (25)
• September 2021 (25)
• August 2021 (41)
• July 2021 (36)
• June 2021 (29)
• May 2021 (29)
• April 2021 (31)
• March 2021 (33)
• February 2021 (28)
• January 2021 (29)
• December 2020 (38)
• November 2020 (40)
• October 2020 (41)
• September 2020 (35)
• August 2020 (38)
• July 2020 (36)
• June 2020 (46)
• May 2020 (42)
• April 2020 (37)
• March 2020 (60)
• February 2020 (39)
• January 2020 (45)
• December 2019 (36)
• November 2019 (35)
• October 2019 (42)
• September 2019 (45)
• August 2019 (56)
• July 2019 (44)
• June 2019 (35)
• May 2019 (40)
• April 2019 (48)
• March 2019 (61)
• February 2019 (39)
• January 2019 (30)
• December 2018 (29)
• November 2018 (51)
• October 2018 (45)
• September 2018 (29)
• August 2018 (49)
• July 2018 (35)
• June 2018 (31)
• May 2018 (39)
• April 2018 (31)
• March 2018 (26)
• February 2018 (33)
• January 2018 (30)
• December 2017 (26)
• November 2017 (24)
• October 2017 (30)
• September 2017 (30)
• August 2017 (32)
• July 2017 (27)
• June 2017 (32)
• May 2017 (26)
• April 2017 (37)
• March 2017 (28)
• February 2017 (30)
• January 2017 (27)
• December 2016 (29)
• November 2016 (24)
• October 2016 (32)
• September 2016 (31)
• August 2016 (27)
• July 2016 (24)
• June 2016 (26)
• May 2016 (19)
• April 2016 (30)
• March 2016 (37)
• February 2016 (27)
• January 2016 (33)
• December 2015 (25)
• November 2015 (23)
• October 2015 (16)
• September 2015 (28)
• August 2015 (28)
• July 2015 (6)
• June 2015 (1)
• May 2015 (2)
• April 2015 (1)
• February 2015 (3)
• January 2015 (1)
• December 2014 (1)
• July 2010 (1)
• October 1991 (1)
• August 1989 (1)
• January 1988 (1)
• December 1983 (1)

Announcements

• 2024 Continental Senior (50+) Chess Championships »
• US Chess to Host Town Hall for Tournament Directors on Sunday, May 5 »
• The Herbert B. Jacklyn Program is Open For 2024-25 Submissions »
• 2024 Scholar-Chessplayer Awards Announced: Six Players Honored at the 2024 National High School Championship »

US CHESS PRESS

Exploring the Knight’s Tour Problem

The Knight’s tour problem is an interesting and challenging puzzle that has fascinated mathematicians for centuries. The problem is to find a sequence of moves for a knight on a chessboard such that the knight visits every square exactly once. This problem has been studied since the 9th century, and has been the subject of much research and speculation.

One of the most interesting aspects of the Knight’s tour problem is that it is not always possible to find a solution. This is because the knight’s movement is constrained by the geometry of the chessboard, and some configurations simply do not allow for a complete tour. However, it has been proven that a Knight’s tour is always possible on a rectangular board whose smaller dimension is at least 5.

For any m x n board with m ≤ n, a Knight’s tour is always possible unless one or more of thee three conditions are met: m = 1 or 2. m = 3 and n = 3, 5, or 6. This means that for most standard chessboards, a Knight’s tour is possible.

However, there are some exceptions to this rule. For example, if a square is removed from the chessboard, it may no longer be possible to find a complete Knight’s tour. This is because the removal of a single square can disrupt the geometry of the chessboard in such a way that it becomes impossible to visit every square.

Despite these challenges, the Knight’s tour problem remains a popular puzzle among mathematicians and puzzle enthusiasts. It is a fascinating example of how mathematics can be used to explore complex problems in a structured and systematic way.

The Knight’s tour problem is an intriguing puzzle that continues to fascinate mathematicians and puzzle enthusiasts alike. While there are some situations where it may not be possible to find a complete tour, the problem remains a challenging and rewarding pursuit for those who enjoy puzzles and problem-solving.

Is The Knight’s Tour Possible?

The Knight’s Tour is possible on a rectangular board whose smaller dimension is at least 5. Additionally, for any m x n board with m ≤ n, a Knight’s Tour is always possible unless one of the following conditions are met: – m = 1 or 2 – m = 3 and n = 3, 5, or 6.

It is important to note that a Knight’s Tour is a sequence of moves made by a knight on a chessboard, where the knight visits every square exactly once. The proof of the existence of a Knight’s Tour on certain types of boards is a well-studied problem in mathematics.

What Is The Knights Tour Theory?

The Knight’s tour theory is a problem in the field of mathematics and chess. The problem is to find a sequence of moves by a knight on a chessboard such that the knight visits every square exactly once. The knight is allowed to move two squares in one direction and one square in the perpendicular direction. The problem has been studied for centuries, and many different solutions have been proposed.

One of the main questions in the Knight’s tour theory is whether a knight’s tour exists for every possible starting position and board size. It has been proven that a knight’s tour exists on all chessboards with one square removed, except for some specific cases. For example, if the board size is even, or if the removed square is (i, j) with i + j odd, then a knight’s tour may not be possible.

Other specific cases whre a knight’s tour may not be possible include when the board size is 3 and any square other than the center square is removed, when the board size is 5, when the board size is 7 and any square other than square (2, 2) or (2, 6) is removed, and when the board size is 9 and a certain specific square is removed.

The Knight’s tour theory is a fascinating problem that has captured the imagination of mathematicians and chess players alike. It is a challenging problem that requires creative thinking and careful analysis, and it continues to be studied and explored by researchers today.

What Is The Knight’s Tour Problem?

The Knight’s Tour problem is a mathematical puzzle that requires a player to find a sequence of moves for a knight piece on a chessboard, such that the knight visits every square exactly once. In other words, the problem asks whethr a knight can move to every square on the chessboard without repeating any square. The knight is allowed to move only in an L-shaped pattern, i.e., two squares horizontally or vertically and then one square in the perpendicular direction. The problem has been studied for centuries and has fascinated mathematicians and chess players alike. It has many applications in computer science, such as in algorithm design and optimization. The Knight’s Tour problem is a classic example of a combinatorial optimization problem, and finding a solution to the problem requires a lot of creativity and strategic planning.

The Knight’s tour problem has been a topic of interest for mathematicians and chess enthusiasts for centuries. While the problem may seem simple at first glance, it presents a challenging puzzle that requires careful analysis and strategic thinking. Through the years, various algorithms and techniques have been developed to solve the problem, and it has been proven that a Knight’s tour is possible on crtain types of chessboards. However, some conditions must be met, and certain squares must not be removed for the tour to be achievable. Despite its difficulty, the Knight’s tour problem remains a fascinating and engaging puzzle that continues to capture the imagination of people from all walks of life.

Doug Barlow

On 26 August 1735, Leonard Euler presented a talk to the Imperial Science Academy that was the basis for his paper, "The solution of a problem relating to the geometry of position." In this work Euler addressed an age-old problem that had for years bewildered the populace of the city of K�nigsberg in East Prussia. The city, as it was in Euler’s time was situated around the River Pregel which divided the city into 4 separate areas all linked together by a system of bridges as shown in the picture below. The problem the people used to ponder was whether or not it was possible to walk around the city crossing each of the seven bridges only once. Of course nobody had ever succeeded but it wasn’t until Euler approached the problem from the viewpoint of a mathematician that it was actually proved. It was from this proof that Euler managed to discover some general rules to apply to other problems of this type. Euler began by producing a topological map or graph of the bridges and their landfall such that the four parts of the city are labelled A, B, C and D, and the bridges are labelled a, b, c, d, e, f and g.

Each of the parts of the city is called a vertex and is connected by the bridges to be called edges . Euler proved that it was not possible to use all the edges once no matter where one begins because in order to do so one must exit each vertex every time it is entered and therefore each vertex requires an even number of edges. As can be seen this is not the case in K�nigsberg, and in fact all the vertices have odd degree or valency . If we were to add just one extra edge ‘h’ between the two vertices B and D it would then be possible to traverse each edge once and once only but we would find ourselves finishing our walk at a vertex other than the one where we began.

We now have vertex C with degree 3 and vertex A with degree 5 but B and D are now both even having degree 4. Because we must always have an entry and an exit edge to find a path through the graph this means that the vertices of odd degree must be the start and finish of the path that exists in this connected graph. If we begin our walk at vertex C and finish at vertex A then our path traverses the edges as follows: - a,g,c,d,b,e,h,f. We have fulfilled the criteria required in that we have travelled each edge once and only once but we have not returned to our starting point. These results give us Euler’s statements from the translation in Graph Theory 1736 - 1936 [2] .

"If there are more than two areas (vertices) to which an odd number of bridges (edges) lead, then such a journey (Eulerian path) is not possible. If, however, the number of bridges (edges) is odd for exactly two areas (vertices), then the journey (Eulerian path) is possible if it starts in either of these areas (vertices). If, finally, there are no areas (vertices) to which an odd number of bridges (edges) lead, then the required journey (Eulerian path) can be accomplished starting from any area (vertex)." (My brackets.)

In this particular paper the definition of an Eulerian path is to be one that covers each edge once and only once but does not necessarily finish on the vertex it began. I’m not sure though how the burghers of K�nigsberg would have felt about not returning home for supper after such a long walk! Euler was a man who loved puzzles and, although I cannot find his original discourse and systematic approach to the Knight’s tour, I am aware through the work of other mathematicians that he did look at the problem. Another mathematician of the time, A. -T. Vandermonde took up the challenge.

Graph Theory (Section II) Back to top

Alexandre - Theophile Vandermonde was a French mathematician who became interested in the problem of, "the twists and turns of a system of threads in space ... and the manner in which the threads are interlaced." How one might annotate the path of the threads in a braid, knot or net and therefore fix for all time a method for recreating these objects was what Vandermonde sought. He considered, "a well-known problem, which belongs to this category, that of the knight’s tour in chess , solved by Euler in 1759." Vandermonde’s "Remarques sur les Problemes de Situation" (Remarks on problems of position), which I shall paraphrase here, begins by outlining his system of notation for the division of space. His method is to first establish a plane of parallel lines that is then cut by a further plane of parallel lines running perpendicular to the first set such that both sets constitute a grid.

We can now see that the shaded square in the above diagram is in the, "fourth strip of the first division and the third in the second division" of the plane. If we compare this system of notation to that of Cartesian co-ordinates then the ‘first division’ produces values of ‘x’ and the second, values of ‘y’. The shaded square can be represented by (4,3) in Cartesian notation. Vandermonde then goes on to cut the plane into a third dimension so that the grid above becomes the face of a cube resting on a table, that one is viewing from above. Thus our shaded square now has co-ordinates 1 and the one below it co-ordinates 2 and so on. The large number at the front of the notation being the depth of each level from our viewpoint. Again using Cartesian co-ordinates we could say that the level is ‘z’ and the shaded square on a cube becomes (z, x, y). Once this method is established the possibility of realising a path through the plane that passes through a series of designated points can now be fixed and Vandermonde goes on to describe the sequence of points for a plait and a stocking-stitch. Having now established the notation for three dimensions we will revert to our original two-dimensional model and look at the knight’s tour on the chessboard. The problem is to find a formula or rule that allows us to satisfy the criteria of the tour and so complete it. The method Vandermonde used was to pick an arbitrary starting point and ‘reflect’ that move in three other positions on the board so as to try and simplify the solution by creating some kind of symmetry. He achieved this by: - First list all possible squares on the board and their corresponding co-ordinates. I.e. 64 sets of co-ordinates.

Choose an arbitrary starting point and remove it from the list of all possible squares. Vandermonde chose . This square becomes the beginning of path list ‘one’. Using successive rotational symmetry of 90 o about the centre of the board create three further path lists of co-ordinates that begin with each of the three rotations’ co-ordinates i.e. , and (see diagram below). Then delete these sets of co-ordinates from the list of all possible squares leaving 60 squares. From the starting point in path list ‘one’ pick an arbitrary knight’s move from this square (such that it is in the remainder of the list of all possible squares) and note this as move 2 in path list ‘one’. Remove it from the list of all possible squares that will now be left with 59 sets of co-ordinates. Repeat the three rotations for move 2 and add them to their respective path lists remembering to delete them from the list of all possible squares leaving 56 sets of co-ordinates. Continue with this process until all squares are used up and there will be four paths lists each of 16 sets of co-ordinates. Vandermonde called these four paths lists his ‘symmetric’ lists of moves.

See diagram below showing the first four moves (in colours) and their ‘symmetries’.

By continuing in this way Vandermonde generated the four sequences of moves as follows: -

From these four sequences of moves Vandermonde noticed that the end of the first sequence was a knight’s move away from the beginning of the fourth and the end of the second a knight’s move away from the start of the third creating two ‘symmetric’ sequences thus: -

In order for the path to be re-entrant, and so become a circuit, he had to find a way to link these two sequences together and destroy his so called ‘symmetry’ a little. By placing the entire second sequence between the third and fourth terms of the first (blue to blue and red to red are knight’s moves apart) he completed his re-entrant tour that can begin at any one of the squares of the sequence. The path generated by this sequence is shown below.

This sequence of moves is just one of many possible circuits for the knight’s tour and also represents a new way of looking at graphs i.e. how is it possible to find a path through a given graph that passes through every vertex once and once only? Of course we know this is possible for the knight’s tour because there are many solutions for the 8 x 8 board but the task of finding an Eulerian path might not be so easy. Here is the graph representing a 4 x 4 chessboard with all-possible vertices and edges.

An Eulerian path must, as we have seen, pass through every edge of a graph once and once only. If one were to look at all possible edges on the 8 x 8 chessboard, we would find that there are eight vertices with odd degree and therefore, according to his rules, no Euler path (See diagram).

This diagram above shows the vertex degree of each square on the chessboard in relation to the knight’s move.

There are 8 vertices with odd degree and therefore no Euler path.

We now have a different class of problems that are commonly known as traveller problems. In Graph Theory [2] (the brackets are mine), "the explorer examines all possible routes (edges), whereas the traveller simply wishes to visit each place of interest (vertex) once." The most common expressions for these two varieties of problems are "The Postman" and "The Travelling Salesman". The Postman needs to minimise the distance he travels while at the same time making sure he delivers mail to all the streets (edges) and he doesn’t want to travel down any streets more than once. The Travelling Salesman needs to visit specific addresses (vertices) each once and only once and again minimise the distance he travels but of course he won’t need to use all the streets in order to do it. The latter is the essence of the knight’s tour although our knight must finish its journey one move away from its starting point in order to make a cycle, or re-entrant tour. When T. P. Kirkman first considered circuits in his 1855 paper, "On the Representation of Polyhedra", he discovered a class of graphs that could not contain circuits and it is this result that we shall move onto next.

Graph Theory (Section III) Back to top

Thomas Penyngton Kirkman was a rector and mathematician who explored the possibility of finding a circuit that passes through each vertex of graph once and only once. His rather complex and ultimately unprovable ideas were later picked up and refined successfully by Sir William Rowan Hamilton but not before Kirkman had managed to provide a general proof for the fact that, "if a polyhedron has an odd number of vertices and each face has an even number of edges, then there is no circuit which passes through all the vertices." [2] . This introduces the concept of a graph being bipartite i.e. if a graph can divided into two separate sets of vertices such that every edge in one set joins a vertex in the other then it is called bipartite. If therefore we require a circuit, which passes through each vertex once and only once, and return to the initial vertex then a graph with an odd number of vertices will have no such circuit. When Euler discussed this question in relation to a chessboard with n x n squares he discovered that if n is odd then there will be an odd number of squares. Since any chessboard is bipartite with two sets of squares black and white, no complete reentrant tour can exist for these boards.

First looking at the path p of the circuit that may exist can prove if the number of vertices n is odd in a bipartite connected graph then no circuit exists. If a graph has n vertices then let the initial vertex be V 0 and the final vertex V n-1 . The path for a circuit through this graph must start at the initial vertex V 0 and pass through all other vertices before reaching the final vertex V n-1 . Because the last vertex must connect to the first V 0 = V n . If the graph is bipartite then the total number of vertices will be V A + V B If we assume that V 0 is in vertex group A so that V 1 is in vertex group B, V 2 is in vertex group A and so on, then all vertices in group A will be even and all in group B will be odd. Because V n must be equal to V 0 if the graph has a circuit it holds that V n must be part of group A and therefore even. By contradiction if a possible circuit exists for even values of n then none can exist if n is odd. At the time Kirkman was looking at polyhedra there was another mathematician, William Rowan Hamilton, who was also working on a similar problem that he published in 1857 as "The Icosian Game." Hamilton’s game consisted of the net for a dodecahedron that had a pin at each of the 20 vertices representing important cities around the world. The problem was to find a route around the shape that passed through each city once and only once. The pins were provided so that a thread could be wound round them and make the path visible.

It was directly due to the concepts involved in this game that a circuit in a graph visiting every vertex once and only once became know as a Hamiltonian Line. The problem that Euler had was using each edge once and only once and really just a case of examining the vertices in a graph to see if they are even but the Hamiltonian problem has no such simple solution and indeed still today has no general criteria.

The Knight’s Tour (Section IV) Back to top

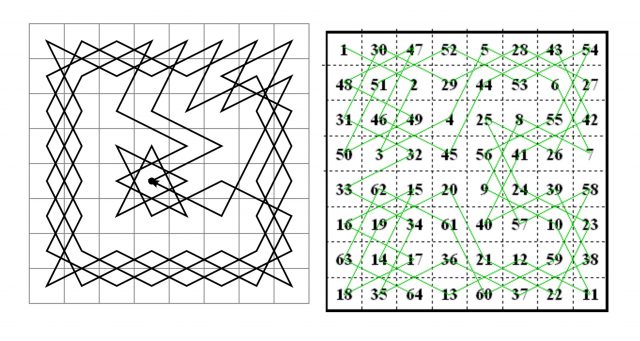
I began looking at this problem from the original question that is, can I find a path through the chessboard, using only the moves of the knight, that uses every square once and only once and finishes one knight’s move away from the starting square. As I sought solutions to the problem I came across many reference sources and literature referring to previous attempts at the problem, that had looked at more general criteria concerning the finding of Hamiltonian circuits within ‘chessboard graphs’ of varying sizes. After discovering programs have been written to look at and solve this question I found they were beyond my understanding at this point and so decided to approach it from the traditional perspective - by hand! I began by finding circuits in the 8 x 8 board using various algorithms that seemed at first most logical to me. The first of which was, "start in the corner, where there are only two possible moves (one to square 1 and the other from square 63) and work one’s way around the board sticking as close to the edge as possible bearing in mind access to square 63." This method produced the following results.

It is worth looking at this basic algorithm more closely to see where it might be improved so as to guarantee success on the first try. The algorithm, as it is, leaves the user with a few choices that could easily result in an unsuccessful solution to the problem. Specifically I first draw your attention to move 2, which originates at square 1 and moves to square 2. The choices at square 1 are two-fold i.e. to move to what actually becomes square 48 or to square 2. In this case the reasoning behind the move is to stay as close to the corner as possible if you have choices. This decision occurs again at square 45, where both options for square 46 are on the edge of the board. However, this time both choices are equidistant from a corner. As it happens either square will do to secure the tour if we stick to the original algorithm of staying as close to the edge as possible. So, apart from the second move, which must stay close to the corner, the algorithm holds. The greatest inadequacy with this algorithm is that it only works if we start in the corner and specify square 63 as our end point. What happens if I apply this algorithm to any starting square? If I arbitrarily use (3, 4) as the initial vertex then... hey presto, it works!

Unfortunately this is just a lucky second choice but does throw up a very interesting question. When using this original algorithm I have not managed to succeed every time, although if I look forward from approximately move 51 and think carefully about each of the options open to me I do succeed every time. The last quarter of the tour does seem to need refining in order to ensure a complete re-entrant tour without having to think. It certainly seems so because lengthy tours by hand using the original algorithm, resulted in many failures. Before considering what this additional statement might say I refer to an algorithm that already exists for non-re-entrant tours called the Warnsdorff algorithm. Warnsdorff’s algorithm involves looking at the valency of each of the next possible vertices (knight’s moves) and choosing that square which has the least degree so that any square likely to be isolated will be used up before isolation occurs. This is all the more logical because no vertex has less than degree 2. The only other stipulation is that if the choices of move all have the same degree then the algorithm will look further down each of the possible avenues of moves applying the least degree rule until a successful successor is found. This algorithm has proved to be very slow for large boards and fails at 76 x 76 squares.In "Solution of the Knight's Hamiltonian Path Problem on Chessboards" [5] , Ingo Wegener and his fellow researchers tried to refine the Warnsdorff system by the addition of a further rule that initially broke the larger board down into smaller sections for which there were already known tours. This is an approach that they were ultimately able to prove but is different to the Warnsdorff method. It is possible to refine the Warnsdorff algorithm so that it fails less often and this was suggested by Arnd Roth in his "Mathematica notebook"  [6]

"To amend this (the choices of move all have the same degree), I add the rule that in this case, the successor with largest Euclidean distance to the centre of the chessboard is chosen. The introduction of this global criterion substantially reduces the number of blind alleys: now it first occurs on a 428 times 428 chessboard, and the "probability" to run into one (a blind alley) is less than one percent for all chessboards smaller than 2000 times 2000 squares. (All this assumes that the starting point is in a corner of the board.)"

So, even the power of Mathematica, that was used to implement Roth’s improved algorithm, has its limitations and with it's starting point restrictions I still feel that I have made a great deal of headway with my simple algorithm. The refined version is now, "Pick an arbitrary starting square and, using the move of the knight choose your next square such that it is as close to the edge of the board as possible making sure that access to the starting square is not blocked. Where there is a choice of squares equidistant from the edge of the board one must consider the subsequent moves from each of those squares such that they must follow the previous rules." This is really about as tight as I can make it for a 8 x 8 board but is also the method I have used to approach other size boards starting with 3 x 3, the smallest board I have looked at. With this 3 x 3 board it is clear to see that no Hamiltonian circuit exists because if we start at the centre square ‘*’ we have no moves to make and if we start in any of the other squares it is impossible to reach the centre.

The 3 x 3 square was not a complete waste of time though because if we add just one extra column then we can start ‘outside’ our 3 x 3 section at ’0’. Then we complete the 3 x 3 line that again moves outside to ‘9’ back to ‘10’ (our previously unreachable square) and finishes at ‘11’. Although this doesn’t satisfy the rules for a re-entrant tour it does still use every vertex once and only once.

I note at this stage that the 3 x 3 square has 1 vertex with degree 0 and 8 vertices with degree 2 and no path or circuit exists. The sum of degrees is 16 and we know that in order for a circuit to exist every vertex must have two edges leading to a sum of 18 for a nine-vertex graph and therefore a circuit cannot exist in this graph. In the 3 x 4 rectangle however there are 8 vertices of degree 2 and 4 of degree 3 giving a total of 28. I now know there are enough edges to fulfil requirements for a circuit but none exist in this graph. I still take note of these results. For a 3 x 5 rectangle there are 8 vertices of degree 2, 4 of degree 3 and 3 of degree 4 giving a total of 40 edges. As there are 15 vertices one would expect a complete tour to have 30 edges and so it may be possible to at least find a path but I could not find one. The vertex degrees are as follows.

The path for a 3 x 6 has eluded me as well and the vertex degrees are: -

The path in the 3 x 7 board is seen to be the incomplete graph of the 3 x 3 board joined to the path of the 3 x 4 board.

Finally in this section the 3 x 8 board has a path constructed from two 3 x 4 paths linked together (see dotted line in diagram below).

I have tabulated the results below to try and uncover a rule for whether or not a path can exist. So far the table looks like this: -

I haven’t managed to formulate a proof for my assumptions but a path does exist in the 3 x 4 board and successfully links to the incomplete path in the 3 x 3 board to provide a path in the 3 x 7 board. If I continue with this hypothesis I can only find paths in boards for which the value of 3 x n can be subdivided into previously successful paths or that provide links to unsuccessful ones.

Squares Only Back to top

If I were to consider just those boards that are n x n then 3 x 3 is my starting point for which, as we have already seen, no path or tour exists. The next square to consider is that of 4 x 4. No path exists for this square and the valency for each vertex is as follows: -

The reason no path can exist for this board is that at least two of the degree 2 squares must have two edges attached and they cannot be in opposite corners or a closed circuit of four vertices would end the game. Therefore if the two start and finish squares are in corners on the same row or column all the degree 4 squares will be unable to take any further edges leaving the insoluble problem of negotiating a path around all the vertex degree 3 squares.

If we now look at the square 5 x 5 : -

As can be seen there is a path for this square, above, though there is no re-entrant tour. However, there is something interesting about this square in that it is the first to have a vertex with degree 8 that occurs in the centre square. Euler proved that in the knight’s tour problem if n is greater than or equal to 5 then a path (not necessarily a re-entrant tour) does exist, however time and workload have made it impossible for me to find it at the time of going to press. I will endeavour to find it at a later date. The circuit I found in the 6 x 6 board was the only one I could find after much searching although I can’t believe at this stage that there is only one. Of course this particular tour can start at any of its 36 squares although I choose to count this as only one knight’s tour.

The 7 x 7 board is, as I have referred to before, bipartite and therefore unable to have a tour though one of the many paths it has is shown below.

I have already looked at 8 x 8 circuits and the information I have discovered about all the n x n squares to this point is consolidated in the table below. There are many obvious patterns in the data though none seems to direct me to any conclusive proof about a general statement regarding the existence of a re-entrant tour in any given n x n board. I am sure that so long as n is even there will be a re-entrant tour however I cannot prove it and without the benefit of a computer I would hate to have to find one for large values of n.

Finally I would like to look at the possibility of extending the knight’s tour problem to finding re-entrant tours in cubes. The first fact to consider is the 3 x3 x 3 cube that has a centre vertex that cannot be reached from any other vertex of the cube, therefore a re-entrant tour cannot exist. The next cube to consider is the 4 x 4 x 4 that does have a re-entrant tour I found by hand. The problem I have is writing an algorithm to ensure success every time and I will have to leave that to a further paper. After I describe the tour using a version of Vandermonde’s original system I will attempt to describe the method I used although I don’t believe it will work every time. I have already described Vandermonde’s system of notation in 3-dimensional objects in section II and how it can be simulated in Cartesian terms, (z, x, y). I will use this altered Cartesian system to describe a re-entrant tour in a 4 x 4 x 4 cube. The notation for the bottom left hand cube in the diagram below is (1, 1, 1) and the top back right cube is (4, 2, 3).

I am currently working on a drawing of this tour in 3-dimensional space but for now it will have to wait. The reader should note at this point that the knight can now move freely in space but must still only move by a factor of (� 2, � 1) or (� 1, � 2) in any direction in 3-dimensional space as long as it stays within the volume of the designated cube. A move from (1, 1, 3) to (3, 2, 3) is an example where values of (z, x, y) satisfy these criteria. The co-ordinate tour starts at VERTEX 0 being (4, 4, 1) with vertex 63 being (2, 4, 2), one knight’s move from the initial vertex.

Of course, in respect of previous discoveries in this paper I know that to look for a tour in a 5 cube would be fruitless because it has an odd number of vertices. However I know that a path exists because it is possible to stack up five 5 x 5 squares to make a cube and therefore just a small matter of locating the link edges between each of the ‘levels.’ This method can also be successfully used to capture the ultimate in 3-dimensional chessboards, the 512-vertex polyhedron that is the 8 x 8 x 8 cube. We already know that the vertices 0 and 64 are one and the same in a re-entrant tour of the regular chessboard and we can use this information to combine the eight levels of the 8 cube into one tour by listing the ‘bridging ‘ vertices thus: -

And (3, 1, 3) is a knight’s move from (1, 1, 4) completing the tour.

Conclusions and Reflections on the Knight’s Tour Back to top

I have had an immense amount of fun and an intensely thought provoking experience in compiling these pages and there are still so many questions. Can I adapt Warnsdorff’s algorithm to find paths and re-entrant tours in cubes for given values of n cubes or (p x q x r) rectangles? Where can I find Euler’s proof for paths in squares of n is greater than or equal to  5? What is the significance of the patterns I found when tabulating some of my data and how can I use this information to draw some definite conclusions? There are so many more questions to ask that I don’t have the space here to go into them but I do realise from my research that I have at least lit upon an area of mathematics that is still unsettled in some areas. There is still today no general criteria for the finding of Hamiltonian circuits in a given graph and maybe my explorations might be of help in that department but as yet I can’t see it. I will try to produce a written English algorithm for my tours in a cube but for the meantime I will add some of my findings to my website because the many people out there who have also been looking at this problem might find it useful. There is a list of references in the Bibliography that I have used in addition to those quoted in the body of this document and I would like to bring special attention to the historical use of knight’s tours in the field of cryptography. As I mentioned before, one of the French mathematicians’ de Moivre’s tours is the favourite to have been used as an encoding device in the ‘The Second Parchment at Rennes-le-Chateau’ that is fascinating reading for any budding Sherlock Holmes’ out there. And finally as a student teacher I would like to point out that the knight’s tour is a great exercise to try in the classroom both for simple educative fun and more extended work as required.

Bibliography and References Back to top

[1] Cranshaw Ted The Second Parchment at Rennes-le-Chateau ( http://www.fiu.edu/~mizrachs/parchmen.htm ) [2] N. L. Biggs, E. K. Lloyd, R. J. Wilson Graph Theory 1736 - 1936 (1976) Oxford, Oxford University Press Beineke & Wilson Graph Connections (1997) London, Clarenden Press [5] A. Conrad, T. Hindrichs, H. Morsy & I. Wegener: Solution of the Knight's Hamiltonian Path Problem on Chessboards . Discr. Appl. Math. 50, 125-134 (1994). John Clark and Derek Allan Holton A first Look at Graph Theory (1991) Singapore, World Scientific [3] Oystein Ore Graphs and their uses (1963) Stanford, California, USA, Random House W. T. Tutte Graph Theory as I have known it (1998) London, Clarenden Press Robin J. Wilson Introduction to Graph Theory (1972) Harlow, Longman Scientific & Technical [6] Arnd Roth's Homepage - Studying physics in Heidelberg he spends a lot of time doing electrophysiologyalthough his main scientific interests are computational physics, computational neuroscience, and software environments for scientific computation, such as Mathematica and NEURON . Other Graph Theory and Related Pages by Stephen C. Locke - This site covers all aspects of Graph Theory in general and is a valuable starting point if you are looking for plenty of link suggestions. Combinatoric Object Server - Not much more I'm afraid but still useful. Paul E. Black - A computer scientist from Maryland, USA who has some great research and links that are an absolute necessity for anyone interested in algorithms and graph theory. Gunno T�rnberg - Thoughts and research on the Travelling Salesman's Problem with other very useful links. A top chap who helped me greatly with the accuracy of these pages of mine. Gunno also has a great Knight's Tour page that is well worth a visit at this address . All material, produced by whatever means in these pages, Copyright � Mark Richard Keen 2000 Please feel free to sign the visitor's book. My Guestbook Back to top

• SUGGESTED TOPICS
• The Magazine
• Newsletters
• Managing Yourself
• Managing Teams
• Work-life Balance
• The Big Idea
• Data & Visuals
• Reading Lists
• Case Selections
• HBR Learning
• Topic Feeds
• Account Settings
• Email Preferences

6 Common Leadership Styles — and How to Decide Which to Use When

• Rebecca Knight

Being a great leader means recognizing that different circumstances call for different approaches.

Research suggests that the most effective leaders adapt their style to different circumstances — be it a change in setting, a shift in organizational dynamics, or a turn in the business cycle. But what if you feel like you’re not equipped to take on a new and different leadership style — let alone more than one? In this article, the author outlines the six leadership styles Daniel Goleman first introduced in his 2000 HBR article, “Leadership That Gets Results,” and explains when to use each one. The good news is that personality is not destiny. Even if you’re naturally introverted or you tend to be driven by data and analysis rather than emotion, you can still learn how to adapt different leadership styles to organize, motivate, and direct your team.

Much has been written about common leadership styles and how to identify the right style for you, whether it’s transactional or transformational, bureaucratic or laissez-faire. But according to Daniel Goleman, a psychologist best known for his work on emotional intelligence, “Being a great leader means recognizing that different circumstances may call for different approaches.”

• RK Rebecca Knight is a journalist who writes about all things related to the changing nature of careers and the workplace. Her essays and reported stories have been featured in The Boston Globe, Business Insider, The New York Times, BBC, and The Christian Science Monitor. She was shortlisted as a Reuters Institute Fellow at Oxford University in 2023. Earlier in her career, she spent a decade as an editor and reporter at the Financial Times in New York, London, and Boston.

Partner Center

• Ethics & Leadership
• Fact-Checking
• Media Literacy
• The Craig Newmark Center
• Reporting & Editing
• Ethics & Trust
• Tech & Tools
• Business & Work
• Educators & Students
• Training Catalog
• Custom Teaching
• For ACES Members
• All Categories
• Broadcast & Visual Journalism
• Fact-Checking & Media Literacy
• In-newsroom
• Memphis, Tenn.
• Minneapolis, Minn.
• St. Petersburg, Fla.
• Washington, D.C.
• Poynter ACES Introductory Certificate in Editing
• Poynter ACES Intermediate Certificate in Editing
• Ethics & Trust Articles
• Get Ethics Advice
• Fact-Checking Articles
• International Fact-Checking Day
• Teen Fact-Checking Network
• International
• Media Literacy Training
• MediaWise Resources
• Ambassadors
• MediaWise in the News

Support responsible news and fact-based information today!

‘Satanic rituals’ at Taylor Swift shows? That’s false. And experts say the attack isn’t new.

Experts say musicians have been accused of performing satanic rituals for decades.

Social media users have their pitchforks and proof, as Taylor Swift lyrics famously say, and they’re hunting for Satan worshippers. The current target? Swift herself.

“Taylor Swift is doing satanic rituals during her shows,” said a man in an  April 12 Facebook reel .

“This is now coming just blatantly,” he said, as footage played of Swift wearing a green cloak surrounded by dancers holding golden orbs. “You’ve got Taylor Swift doing all kinds of witchcraft rituals and satanic stuff on stage.”

Then he showed a clip from Swift’s “Karma” music video, saying: “It shows Taylor Swift in what appears to be hell wearing what appears to be a devil mask.”

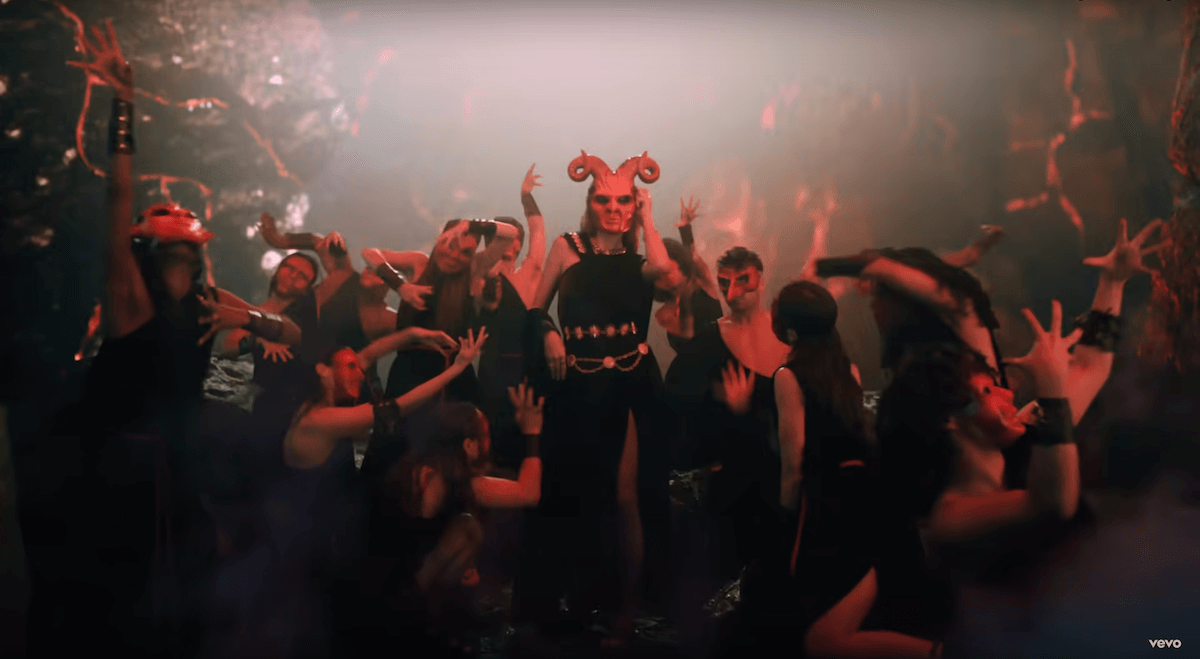
Taylor Swift holds a red mask with horns in front of her face the “Karma” music video. (Screenshot/YouTube)

“Nice devil mask there, Taylor Swift,” he said. “Why the devil mask? Why this kind of imagery?”

In another Facebook  video , a man claimed one of Swift’s hand gestures during her Eras Tour show was the singer “throwing up the devil horns.”

These posts were flagged as part of Meta’s efforts to combat false news and misinformation on its News Feed. (Read more about our  partnership with Meta , which owns Facebook and Instagram.)

Swift’s catalog of lyrics includes mentions of witches, devils and angels. She sings, “Women like hunting witches, too,” in “Mad Woman” from her 2020 album “Folklore.” In the 2019 song “Cruel Summer,” she sings, “Devils roll the dice, angels roll their eyes.” We found no mentions of Satan, Lucifer or satanic rituals.

Although some critics have  claimed  her Eras Tour performance of the song “Willow” promotes witchcraft, we found no evidence that Swift’s performances intentionally feature satanic rituals. The “Willow” dance appears to be a stage adaptation of a similar scene from her  music video .

There is  no clear evidence  Satan worship has ever  been practiced  in an organized and widespread way, so it isn’t clear what “Satanic rituals” the post claimed Swift was performing.

Lucien Greaves, co-founder of The Satanic Temple, a religious organization that the IRS recognizes as a tax-exempt church, said that he sees public concern raised about celebrities and alleged satanism almost every month. He called claims like these “incredibly asinine conspiracy theories.”

What would a “satanic ritual” even look like? It’s not clear. The Satanic Temple’s frequently asked questions  page says  the group does not worship Satan or believe Satan — or anything “supernatural” — exists. There is no sacred scripture nor any required rituals. It is a religion because it  provides  “a sense of identity, culture, community, and shared values,” the website says.

Some members may perform rituals they find “personally meaningful” and that are tailored to their individual needs, the  FAQ page  said. Such rituals may include “unbaptisms,” in which people renounce superstitions imposed on them without consent, and destruction rituals, in which people destroy an object they own that symbolizes a source of pain.

We found no evidence that Swift has engaged in any of those activities. She has publicly described herself as a Christian.

In the 2020 documentary “Miss Americana,” she expressed frustration with the policy positions of then-Senate candidate Marsha Blackburn, R-Tenn. (Swift endorsed Blackburn’s  democratic opponent  in 2018; Blackburn was elected in November 2018.)

“Those aren’t ‘Tennessee Christian values,’” Swift said. “I live in Tennessee. I am Christian. That’s not what we stand for.”

Still, like a line from Swift’s “Reputation” album — “they’re burning all the witches, even if you aren’t one” — the lack of evidence hasn’t stopped social media claims linking Swift to satanism or devil worship.

Swift previously appeared to poke fun at the witchcraft attacks. In November, she shared  a video  captured during a performance, when she was singing about an airplane and a plane happened to fly overhead at the open-air stadium, with the caption, “Never beating the sorcery allegations.”

Never beating the sorcery allegations ✨🛬✨ pic.twitter.com/d0mlvF4gZW — Taylor Swift (@taylorswift13) November 13, 2023

We contacted Swift’s spokesperson and received no reply.

A history of musicians facing satanism accusations

Experts told PolitiFact that musicians have long been accused of performing satanic rituals.

“When someone goes looking for signs of satanic ritual, they will find those signs everywhere, from the packaging on products they buy to stop signs,” said Susan Campbell, a distinguished lecturer in the University of New Haven’s Department of Communication, Film and Media Studies.

Joseph Uscinski, a University of Miami political science professor who studies conspiracy theories, agreed that “people see what they want to see.”

“There is a long history of satanic panics in the United States,” Uscinski said. In the 1980s, “all of my favorite bands were accused of taking part in satanic rituals: Led Zeppelin, Ozzy Osbourne, Motley Crue, Iron Maiden.”

Campbell said fans of the rock band Kiss might recall warnings that the band’s name stood for “Knights In Satan’s Service” and related rumors that listeners were “guilty of worshiping Satan.”

“Love the band, hate the band, there is no evidence that members or fans of Kiss worship the devil,” Campbell said.

Campbell said she thinks that Swift’s  2020 endorsement  of President Joe Biden and her  success in encouraging  her fans to register to vote “opened the door for people” to falsely attack her.

“The better approach when faced with such nonsense is a fairly simple two-step process,” Campbell said. “1. Consider the source of these rumors and 2. Do a little digging for yourself.”

A Facebook post says, “Taylor Swift is doing satanic rituals during her shows.”

Swift’s songs mention neither Satan nor Satanic rituals. Swift has publicly described herself as a Christian.

The leader of The Satanic Temple dismissed the allegations about Swift as conspiracy theories, and there is no clear evidence Satan worship has ever been practiced in an organized and widespread way.

At PolitiFact, the burden of proof is on the speaker. Absent proof, we rate this claim False.

This fact check was originally published by PolitiFact , which is part of the Poynter Institute. See the sources for this fact check here .

Opinion | Everyday sexism has no place in sports journalism

The conversation around Gregg Doyel’s comments to Caitlin Clark failed to address larger, systemic issues that could lead to better journalism

Poynter Journalism Prizes honor excellence in U.S. journalism

Winners and finalists are the first for the contest under the stewardship of the Poynter Institute

Here are the winners of the inaugural Poynter Journalism Prizes

The awards continue a 45-year tradition that was most recently headed by the News Leaders Association.

Opinion | An unsettling look at Donald Trump’s social media rants

The former president’s social media audience has diminished since 2021, but his posts — mostly on Truth Social — have only gotten more disturbing

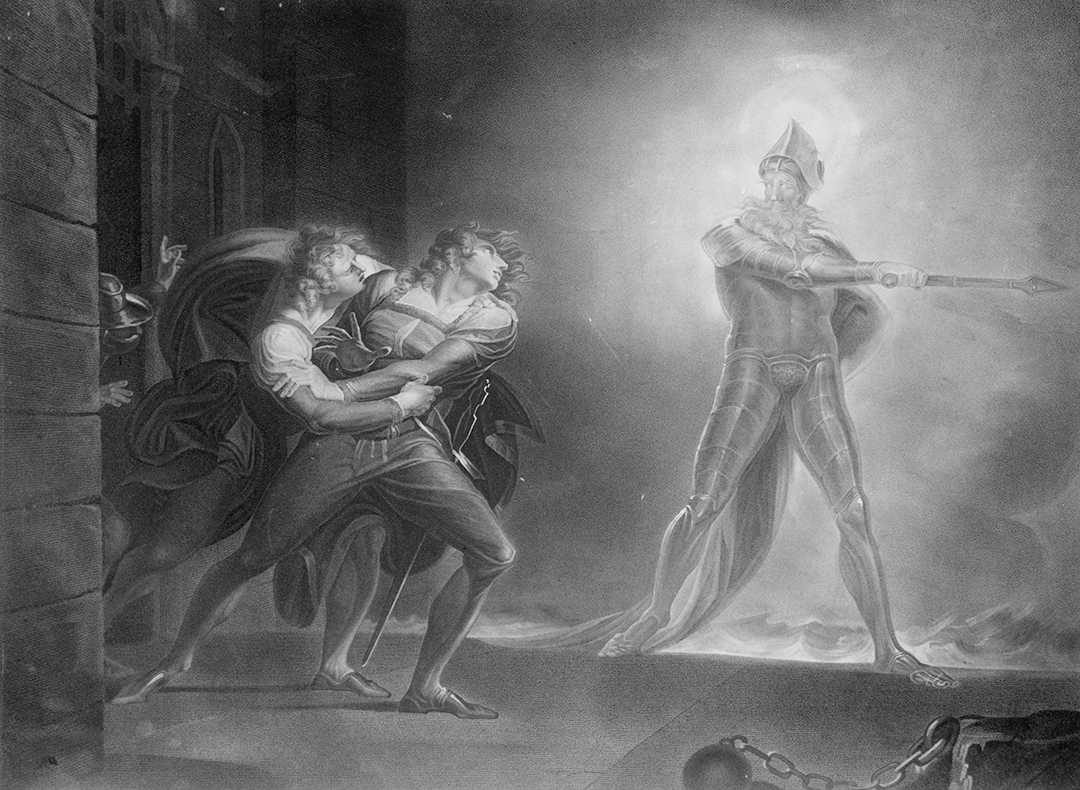
Shakespeare and the power of wordplay … featuring the pun that launched my career

Four words from Hamlet collide with multiple meanings and offer a stimulant for the brain as strong as the most sophisticated puzzle

You must be logged in to post a comment.

This site uses Akismet to reduce spam. Learn how your comment data is processed .

Start your day informed and inspired.

Get the Poynter newsletter that's right for you.